Корень n-ой степени из действительного числа /qualihelpy

Корень n-ой степени из действительного числа

Справочник / Абитуриент / Числовые множества /

Справочный материал Примеры Обратите внимание! Видео Модели Пройти тесты

Корнем n-ной степени, где LaTeX formula: n – натуральное число и $LaTeX formula: n\ge 2$ , из числа LaTeX formula: a называют такое число LaTeX formula: b , n-я степень которого равна .

Записывают: $LaTeX formula: \sqrt[n]{a}$ или $LaTeX formula: a^{\frac{1}{n}$ . Тогда, если $LaTeX formula: \sqrt[n]{a}=b$ , то LaTeX formula: b^n=a .

Число LaTeX formula: a называют подкоренным выражением, а число LaTeX formula: n – показателем корня.

Неотрицательный корень n-ной степени из неотрицательного числа LaTeX formula: a называют арифметическим корнем n-ной степени из числа .
Например: $LaTeX formula: \sqrt[4]{0,0001}=0,1$ ; $LaTeX formula: \sqrt[5]{32}=2$ .

Если показатель корня четное число, то подкоренное выражение не может быть отрицательным числом, так как четная степень и положительного и отрицательного числа есть число положительное.
Если показатель корня равен числу LaTeX formula: 2 , то имеем корень второй степени или квадратный корень из неотрицательного числа LaTeX formula: a , который принято обозначать $LaTeX formula: \sqrt{a}$ или $LaTeX formula: a^{\frac{1}{2}}$ .
Например: $LaTeX formula: \sqrt{100}=10$ ; $LaTeX formula: 81^{0,5}=9$ .

Если показатель корня нечетное число, то подкоренное выражение может быть положительным числом, отрицательным числом и числом нуль.
Если показатель корня равен числу LaTeX formula: 3 , то имеем корень третьей степени или кубический корень из числа LaTeX formula: a , который принято обозначать $LaTeX formula: \sqrt[3]{a}$ .
Например: $LaTeX formula: \sqrt[3]{-1}=-1$ ; $LaTeX formula: \sqrt[3]{0,008}=0,2$ .

Свойства корней:

$LaTeX formula: \sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}$ ; (1.16) $LaTeX formula: \sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}=a^{\frac{1}{mn}}$ ; (1.17)

$LaTeX formula: \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}=\left ( \frac{a}{b} \right )^{\frac{1}{n}}$ ; (1.18) $LaTeX formula: \sqrt[2n]{a^{2n}}=\left | a \right |$ ; (1.19)

$LaTeX formula: \sqrt[2n+1]{a^{2n+1}}=a$ ; (1.20) $LaTeX formula: \sqrt[n]{a}=\sqrt[kn]{a^{k}}$ . (1.21)

При четном значении LaTeX formula: n свойства 1.16, 1.17 и 1.21 справедливы, если значения LaTeX formula: a и LaTeX formula: b неотрицательные, а свойство 1.18 справедливо, если к тому же при $LaTeX formula: b\ne 0$ .
Свойства 1.19 и 1.20 справедливы при любых значениях и .
Например: $LaTeX formula: \sqrt{5}\sqrt{45}=\sqrt{5\cdot 5\cdot 9}=15$ ; $LaTeX formula: \sqrt[5]{(-3)^5}=-3$ ; $LaTeX formula: \sqrt[6]{(-3)^6}=|-3|=3$ .

Внесение множителя под знак корня

1. Если показатель корня нечетное число, то для любого числа LaTeX formula: a

и натурального числа LaTeX formula: n

справедливо равенство:
$LaTeX formula: a\sqrt[2n+1]{b}=\sqrt[2n+1]{a^{2n+1}b}$ . (1.22)
Например, $LaTeX formula: -2a\sqrt[3]{b}=\sqrt[3]{-8a^{3}b}$ .

2. Если показатель корня четное число, то для любого числа LaTeX formula: a>0 и натурального числа LaTeX formula: n справедливо равенство:
$LaTeX formula: a\sqrt[2n]{b}=\sqrt[2n]{a^{2n}b}$ . (1.23)
Например, $LaTeX formula: 2\sqrt[4]{b}=\sqrt[4]{16b}$ .

3. Если показатель корня четное число, то для любого числа LaTeX formula: a<0 и натурального числа LaTeX formula: n справедливо равенство:
$LaTeX formula: a\sqrt[2n]{b}=-\sqrt[2n]{a^{2n}b}$ . (1.24)
Например, $LaTeX formula: -2\sqrt[4]{b}=-\sqrt[4]{16b}$ .

Вынесение множителя из-под знака корня

1. Если показатель корня нечетное число, то справедливо равенство:
$LaTeX formula: \sqrt[2n+1]{a^{2n+1}b}= a\cdot \sqrt[2n+1]{b}$ . (1.25)
Например, $LaTeX formula: \sqrt[3]{a^5b^6}=ab^2\sqrt[3]{a^2}$ .

2. Если показатель корня четное число, то справедливо равенство:
$LaTeX formula: \sqrt[2n]{a^{2n}b}= |a|\cdot \sqrt[2n]{b}$ . (1.26)
Например, $LaTeX formula: \sqrt{a^5b^6}=a^2|b|^3\sqrt{a}$ .

Сравнение выражений, содержащих корни

1. Если LaTeX formula: a>b>0 , то $LaTeX formula: \sqrt[n]{a}>\sqrt[n]{b}$ .
Например, $LaTeX formula: \sqrt{7}>\sqrt{6}$ .

2. Если LaTeX formula: a>1 и LaTeX formula: n<m , то $LaTeX formula: \sqrt[n]{a}>\sqrt[m]{a}$ .
Например, $LaTeX formula: \sqrt{3}>\sqrt[4]{3}$ .

3. Если LaTeX formula: 0<a<1 и LaTeX formula: n<m , то $LaTeX formula: \sqrt[n]{a}<\sqrt[m]{a}$ .
Например, $LaTeX formula: \sqrt{0,3}<\sqrt[4]{0,3}$ .

4. Чтобы сравнить числа $LaTeX formula: \sqrt[m]{a}$ и $LaTeX formula: \sqrt[n]{b}$ , необходимо представить их в виде корня одной и той же степени.

5. Чтобы сравнить числа LaTeX formula: a и $LaTeX formula: \sqrt[n]{b}$ необходимо представить число в виде $LaTeX formula: \sqrt[n]{a^n}$ .

Степень с действительным показателем

Степени с действительным показателем обладают всеми свойствами степеней с целым показателем.
При этом следует помнить, что:

а) степень числа с натуральным показателем имеет смысл для любого основания, так как эта степень определяется с помощью операции умножения;

б) степень с целым отрицательным показателем имеет смысл для любого основания, кроме основания LaTeX formula: 0 , так как эта степень определяется с помощью операций умножения и деления;

в) степень с рациональным показателем определяется с помощью операции извлечения корня, которая всегда выполнима, если основание степени положительное число и не всегда выполнима, если основание степени отрицательное число;

г) степень с любым действительным показателем всегда определена, если ее основание – положительное число.

Среднее арифметическое и среднее геометрическое

Чтобы найти среднее арифметическое нескольких чисел необходимо сумму этих чисел разделить на их количество.
Например, среднее арифметическое чисел 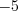LaTeX formula: -5 , LaTeX formula: -1 и LaTeX formula: 12 равно:
LaTeX formula: (-5-1+12):3=2 .

Чтобы найти среднее геометрическое LaTeX formula: n положительных чисел, необходимо извлечь корень степени из произведения этих чисел.
Например, среднее геометрическое чисел LaTeX formula: 1 , LaTeX formula: 4 , и LaTeX formula: 54 равно:
$LaTeX formula: \sqrt[3]{1\cdot 4\cdot 54}=\sqrt[3]{2^2\cdot 2\cdot 3^3}=2\cdot 3=6$ .

Пример 1. Найдите значение выражения $LaTeX formula: \frac{\sqrt[4]{3}}{\sqrt{\sqrt{48}}}+\left(-2^0\cdot \sqrt[8]{(-3)^8}\right)^2$ .
Решение. Применяя формулы 1.17 и 1.18, получим:
$LaTeX formula: \sqrt[4]{\frac{3}{48}}+\left(-1\cdot |-3|\right)^2={\sqrt[4]{\frac{1}{16}}+9=0,5+9=9,5$ .

Ответ: LaTeX formula: 9,5 .

Пример 2. Упростите выражение $LaTeX formula: \frac{\sqrt[4]{-16a^4b^5}}{2b}$ .

Решение. Так как выражение, записанное под знаком корня четной степени, неотрицательное, то LaTeX formula: b<0 .
Применяя формулу 1.24, получим:

$LaTeX formula: \frac{2|a|\cdot|b|\sqrt[4]{-b}}{2b}=\frac{-b|a|\sqrt[4]{-b}}{b}=-|a|\sqrt[4]{-b}$ .

Ответ: $LaTeX formula: -|a|\sqrt[4]{-b}$ .

Пример 3. Сравните числа: $LaTeX formula: 2\sqrt{7}$ и LaTeX formula: 6 ; $LaTeX formula: \sqrt{5}$ и $LaTeX formula: \sqrt[3]{10}$ .

Решение.
1. Так как $LaTeX formula: 2\sqrt{7}=\sqrt{4\cdot 7}=\sqrt{28}$ , а $LaTeX formula: 6=\sqrt{36}$ и $LaTeX formula: \sqrt{28}<\sqrt{36}$ , то $LaTeX formula: 2\sqrt{7}<6$ .

2. Так как $LaTeX formula: \sqrt{5}=\sqrt[6]{5^3}=\sqrt[6]{125}$ , а $LaTeX formula: \sqrt[3]{10}=\sqrt[6]{10^2}=\sqrt[6]{100}$ и $LaTeX formula: \sqrt[6]{125}>\sqrt[6]{100}$ , то $LaTeX formula: \sqrt{5}>\sqrt[3]{10}$ .

Ответ: $LaTeX formula: 2\sqrt{7}<6$ ; $LaTeX formula: \sqrt{5}>\sqrt[3]{10}$ .

Пример 4. Упростите выражение $LaTeX formula: A=\sqrt[3]{4\sqrt[4]{32}}+\sqrt[3]{9\sqrt[4]{162}}$ .
Решение.
Разложим числа 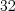LaTeX formula: 4 , LaTeX formula: 32 , LaTeX formula: 9 и LaTeX formula: 162 на простые множители:
LaTeX formula: 4=2^2 , LaTeX formula: 32=2^5 , LaTeX formula: 9=3^2 , $LaTeX formula: 162=2\cdot 3^4$ .

Получим: $LaTeX formula: A=\sqrt[3]{2^2\sqrt[4]{2^5}}+\sqrt[3]{3^2\sqrt[4]{2\cdot 3^4}}$ .

Применим формулу 1.17:
$LaTeX formula: A=2^{\frac{2}{3}}\cdot 2^{\frac{5}{12}}+3^{\frac{2}{3}}\cdot 2^{\frac{1}{12}}\cdot 3^{\frac{1}{3}}$ .
Применим свойство степеней $LaTeX formula: a^n\cdot a^m=a^{n+m}$ :
$LaTeX formula: A= 2^{\frac{13}{12}}+2^{\frac{1}{12}}\cdot 3$ .
Вынесем за скобки общий множитель:
$LaTeX formula: A= 2^{\frac{1}{12}}(2+3)=5\cdot 2^{\frac{1}{12}}$ .

Ответ: $LaTeX formula: 5\cdot 2^{\frac{1}{12}}$ .

1. Среднее арифметическое можно находить как положительных, так и неположительных чисел. Среднее геометрическое чисел находят только в случае, если оба числа положительные.

2. Среднее арифметическое двух положительных чисел LaTeX formula: a и LaTeX formula: b не меньше их среднего геометрического:
$LaTeX formula: (a+b):2\ge \sqrt{ab}$ .

3. Корни четной степени можно извлекать только из неотрицательных чисел, а нечетной степени – и из отрицательных чисел.

4. Корень n-ной степени из числа нуль всегда равен числу нуль.

Программа для просмотра моделей (МК-плеер) Файлы для скачивания М_11_Корень_n-ой_степени