Иррациональными называют уравнения,
содержащие переменную под знаком радикала.
Область определения
(область допустимых значений)
иррационального уравнения состоит из тех значений переменной, при которых
неотрицательны все выражения, стоящие под знаками радикалов четной степени. Если радикал записан в знаменателе дроби, то выражения, стоящие под знаком
радикала четной степени, должны быть положительными.
Методы решений
иррациональных уравнений
1. Метод подстановки.
2. Метод «уединения» радикала, который состоит в том, что, оставляя
радикал в одной части уравнения, возводят обе части уравнения в соответствующую
степень до тех пор, пока не получат уравнение не содержащее радикалов. При
возведении в четную степень необходимо помнить, что обе части уравнения не
должны быть отрицательными.
 , то, возведя обе его части в квадрат (в общем случае в любую четную степень) при условии, что
, то, возведя обе его части в квадрат (в общем случае в любую четную степень) при условии, что  , получим
, получим  .
. то заменим его уравнением
то заменим его уравнением  при условии, что
при условии, что  «Уединим» радикал, приведем подобные слагаемые, опять «уединим» радикал и возведем обе части полученного уравнения в квадрат при условии, что они не отрицательны.
«Уединим» радикал, приведем подобные слагаемые, опять «уединим» радикал и возведем обе части полученного уравнения в квадрат при условии, что они не отрицательны. 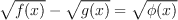 , то при условии, что
, то при условии, что  запишем его в виде
запишем его в виде  и возведем обе части в квадрат. Затем «уединим» радикал, приведем подобные слагаемые и опять возведем в квадрат с учетом вновь возникающих ограничений на переменную.
и возведем обе части в квадрат. Затем «уединим» радикал, приведем подобные слагаемые и опять возведем в квадрат с учетом вновь возникающих ограничений на переменную.![\sqrt[3]{f(x)}+\sqrt[3]{g(x)}=\phi (x), LaTeX formula: \sqrt[3]{f(x)}+\sqrt[3]{g(x)}=\phi (x),](/uploads/formulas/c4b64b00f7393973a0a63cbc0e4374ff8ca1bf26.1.1.png) то запишем его в виде
то запишем его в виде ![\sqrt[3]{f(x)}=\phi (x)-\sqrt[3]{g(x)} LaTeX formula: \sqrt[3]{f(x)}=\phi (x)-\sqrt[3]{g(x)}](/uploads/formulas/ba700990fbd32a60a4c068ecd29faf14bbdbb87f.1.1.png) и возведем обе его части в третью степень:
и возведем обе его части в третью степень: ![f(x)=\left (\phi (x)-\sqrt[3]{g(x)} \right )^3 LaTeX formula: f(x)=\left (\phi (x)-\sqrt[3]{g(x)} \right )^3](/uploads/formulas/e35df33563729ca9b1861ae8de30350d977f186d.1.1.png) . Далее, как правило, применяется подстановка
. Далее, как правило, применяется подстановка ![\sqrt[3]{g(x)} \right =a LaTeX formula: \sqrt[3]{g(x)} \right =a](/uploads/formulas/d21fd4351ac3c22b68ef841f6b937d5fab37d7b1.1.1.png) .
.  строго возрастает, а функция
строго возрастает, а функция  строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение
строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение  на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем.
на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем. . Так как левая часть этого уравнения представлена строго возрастающей функцией, а правая – строго убывающей функцией, то графики этих функций имеют не более одной точки пересечения. Проверкой убедимся, что
. Так как левая часть этого уравнения представлена строго возрастающей функцией, а правая – строго убывающей функцией, то графики этих функций имеют не более одной точки пересечения. Проверкой убедимся, что  . Получим:
. Получим:  ,
,  .
. ![\sqrt[5]{(5x+2)^3}-6=\frac{16}{\sqrt[5]{(5x+2)^3}} LaTeX formula: \sqrt[5]{(5x+2)^3}-6=\frac{16}{\sqrt[5]{(5x+2)^3}}](/uploads/formulas/8f687d2f97aec81af6025a6ba68af5658402ed41.1.1.png) .
.![\sqrt[5]{(5x+2)^3}=a LaTeX formula: \sqrt[5]{(5x+2)^3}=a](/uploads/formulas/26e352415fca1ffa55943d88fb4b24ba77305588.1.1.png)
 , получим:
, получим: или
или  , откуда
, откуда  .
.![\sqrt[5]{(5x+2)^3}=a LaTeX formula: \sqrt[5]{(5x+2)^3}=a](/uploads/formulas/26e352415fca1ffa55943d88fb4b24ba77305588.1.1.png) , решим два уравнения:
, решим два уравнения:![\sqrt[5]{(5x+2)^3}=-2 LaTeX formula: \sqrt[5]{(5x+2)^3}=-2](/uploads/formulas/612446bd84fd9a31c9886eb4d52fadd2e92b9b72.1.1.png) ,
,  ,
,  ,
,  ,
, ![5x=-2\sqrt[3]{4}-2 LaTeX formula: 5x=-2\sqrt[3]{4}-2](/uploads/formulas/e43f78bbbde30f66890b9a0441564736ca2887fc.1.1.png) ,
, ![5x=-2(1+\sqrt[3]{4}) LaTeX formula: 5x=-2(1+\sqrt[3]{4})](/uploads/formulas/742e00d21d1ec9198b6133f58f1d483647d53e54.1.1.png) ,
, ![x=-0,4(1+\sqrt[3]{4}) LaTeX formula: x=-0,4(1+\sqrt[3]{4})](/uploads/formulas/c9dc538206bf821d75084ce900d8de3aa902c9be.1.1.png) ;
;![\sqrt[5]{(5x+2)^3}=8 LaTeX formula: \sqrt[5]{(5x+2)^3}=8](/uploads/formulas/4b741ad0ed4de02d8bacdd6b4b197496af7e503c.1.1.png) ,
,  ,
,  ,
,  .
. Ответ:
![x_{1}=-0,4(1+\sqrt[3]{4}) LaTeX formula: x_{1}=-0,4(1+\sqrt[3]{4})](/uploads/formulas/aa33045db89b772d819d414d5318e02aa0b09553.1.1.png) ,
,  .
.![\sqrt{x^3+8}+\sqrt[4]{x^3+8}-6=0 LaTeX formula: \sqrt{x^3+8}+\sqrt[4]{x^3+8}-6=0](/uploads/formulas/304c283e076f25d731237c92be0e18c92ec551e3.1.1.png) .
. ![\sqrt[4]{x^3+8}=a LaTeX formula: \sqrt[4]{x^3+8}=a](/uploads/formulas/81eeb335b046c0541e74f1f82afcd3cbe6a682a4.1.1.png) и
и  , получим:
, получим: , откуда
, откуда 
Учитывая подстановку
![\sqrt[4]{x^3+8}=a LaTeX formula: \sqrt[4]{x^3+8}=a](/uploads/formulas/81eeb335b046c0541e74f1f82afcd3cbe6a682a4.1.1.png) , решим уравнение:
, решим уравнение:![\sqrt[4]{x^3+8}=2 LaTeX formula: \sqrt[4]{x^3+8}=2](/uploads/formulas/488069b1e3ed88367e34dea659e6a2faab38a2b0.1.1.png) . Тогда
. Тогда  , откуда
, откуда 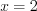 .
. Ответ:
 .
.![\sqrt{x\sqrt[5]{x}}=\sqrt[5]{x\sqrt{x}}+56 LaTeX formula: \sqrt{x\sqrt[5]{x}}=\sqrt[5]{x\sqrt{x}}+56](/uploads/formulas/84db07dad023f90aa9a0eee6e86c972b2b699006.1.1.png) .
. или
или  .
.  , получим:
, получим: , откуда
, откуда  .
. 
 , найдем значение
, найдем значение  :
:  ,
,  ,
,  .
.Ответ:
 .
.![\frac{\sqrt{x}+\sqrt[3]{x}}{\sqrt{x}-\sqrt[3]{x}}=\frac{3}{4} LaTeX formula: \frac{\sqrt{x}+\sqrt[3]{x}}{\sqrt{x}-\sqrt[3]{x}}=\frac{3}{4}](/uploads/formulas/71a318b5f5ff2e750db914098919a16a3c93ebf5.1.1.png) .
.![\frac{\sqrt[6]{x^3}+\sqrt[6]{x^2}}{\sqrt[6]{x^3}-\sqrt[6]{x^2}}=\frac{3}{4} LaTeX formula: \frac{\sqrt[6]{x^3}+\sqrt[6]{x^2}}{\sqrt[6]{x^3}-\sqrt[6]{x^2}}=\frac{3}{4}](/uploads/formulas/d08cc693b8e4df63e84c66808c32c029abf8ca62.1.1.png) .
. ![\sqrt[6]{x}=a LaTeX formula: \sqrt[6]{x}=a](/uploads/formulas/6683af1c347c1dd5c9721342207765bd820ba65c.1.1.png)
 получим:
получим:  ,
,  ,
,  ,
,  ,
,  .
.![\sqrt[6]{x}=-7 LaTeX formula: \sqrt[6]{x}=-7](/uploads/formulas/8897cb5c62def5b43687b421c89113d938e3a155.1.1.png) корней не имеет.
корней не имеет. Ответ:
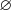 .
. .
. , получим:
, получим: .
. , запишем:
, запишем: или
или  .
. или
или  , откуда
, откуда  .
. , то решим уравнение
, то решим уравнение  .
. Тогда
 или
или  , откуда по теореме Виета
, откуда по теореме Виета  .
. Ответ:
 .
. .
.


 ,
,  .
. :
:  ,
,  , откуда
, откуда  ,
,  .
.  – посторонний корень уравнения, то данное уравнение имеет единственный корень
– посторонний корень уравнения, то данное уравнение имеет единственный корень  .
. Ответ:
 .
.![\sqrt[3]{6+\sqrt{x-1}}+\sqrt[3]{3-\sqrt{x-1}} -3=0 LaTeX formula: \sqrt[3]{6+\sqrt{x-1}}+\sqrt[3]{3-\sqrt{x-1}} -3=0](/uploads/formulas/b42161b4de747fda88e17df7a57b41f0be485db5.1.1.png) .
.![\sqrt[3]{6+\sqrt{x-1}}=3-\sqrt[3]{3-\sqrt{x-1}} LaTeX formula: \sqrt[3]{6+\sqrt{x-1}}=3-\sqrt[3]{3-\sqrt{x-1}}](/uploads/formulas/3e2050f855af0425d4b53dc45d474c8da631d9a8.1.1.png) .
. Возведем обе его части в куб:
![\left (\sqrt[3]{6+\sqrt{x-1}}\right )^3=\left (3-\sqrt[3]{3-\sqrt{x-1}}\right )^3, LaTeX formula: \left (\sqrt[3]{6+\sqrt{x-1}}\right )^3=\left (3-\sqrt[3]{3-\sqrt{x-1}}\right )^3,](/uploads/formulas/144b2e51643aa7e00babfc35f40bcb497eaf4e01.1.1.png)
![6+\sqrt{x-1}=27-27\sqrt[3]{3-\sqrt{x-1}}+9\left (\sqrt[3]{3-\sqrt{x-1}} \right )^2- LaTeX formula: 6+\sqrt{x-1}=27-27\sqrt[3]{3-\sqrt{x-1}}+9\left (\sqrt[3]{3-\sqrt{x-1}} \right )^2-](/uploads/formulas/dbb293a9a4ec1aabf0c14feea718a467aa771409.1.1.png)

![\left (\sqrt[3]{3-\sqrt{x-1}} \right )^2-3\sqrt[3]{3-\sqrt{x-1}}+2=0. LaTeX formula: \left (\sqrt[3]{3-\sqrt{x-1}} \right )^2-3\sqrt[3]{3-\sqrt{x-1}}+2=0.](/uploads/formulas/2005a0fc688abf910638f324c3cbd5c676e76e17.1.1.png)
![\sqrt[3]{3-\sqrt{x-1}} \right )=a LaTeX formula: \sqrt[3]{3-\sqrt{x-1}} \right )=a](/uploads/formulas/f13645cc264ae1a1a32ffead51abe01ae06fe191.1.1.png) .
.  получим:
получим:  .
.![\sqrt[3]{3-\sqrt{x-1}} \right )=a LaTeX formula: \sqrt[3]{3-\sqrt{x-1}} \right )=a](/uploads/formulas/f13645cc264ae1a1a32ffead51abe01ae06fe191.1.1.png) , решим два уравнения:
, решим два уравнения:![\sqrt[3]{3-\sqrt{x-1}} \right )=1 LaTeX formula: \sqrt[3]{3-\sqrt{x-1}} \right )=1](/uploads/formulas/c45282582ca155446858a62dc086dfd912ae8ddc.1.1.png) ,
, ![\left (\sqrt[3]{3-\sqrt{x-1}} \right ) \right )^3=1^3 LaTeX formula: \left (\sqrt[3]{3-\sqrt{x-1}} \right ) \right )^3=1^3](/uploads/formulas/4c02f3d056f36f28e67b9ef37a7d042ae7e0e23d.1.1.png) ,
,  ,
,  ,
, 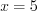 ;
;![\sqrt[3]{3-\sqrt{x-1}} \right )=2 LaTeX formula: \sqrt[3]{3-\sqrt{x-1}} \right )=2](/uploads/formulas/a781b973ba52dc0c176f87bc6d94cd30699a3448.1.1.png) ,
, ![\left (\sqrt[3]{3-\sqrt{x-1}} \right )\right )^3=2^3 LaTeX formula: \left (\sqrt[3]{3-\sqrt{x-1}} \right )\right )^3=2^3](/uploads/formulas/c8c69be03d8ceee74cc492de661064251578b3d7.1.1.png) ,
,  ,
, 
Ответ:
 .
.![\sqrt{x+2}=\sqrt[3]{3x+2} LaTeX formula: \sqrt{x+2}=\sqrt[3]{3x+2}](/uploads/formulas/09f315e9d3c35cacab26e2d8c24100827ec6ce57.1.1.png) .
. и
и ![\sqrt[3]{3x+2}=b LaTeX formula: \sqrt[3]{3x+2}=b](/uploads/formulas/683b75660ce1647ff19bc9494f9f191e9637e8c1.1.1.png) , получим:
, получим: 
Тогда

![\sqrt{x+2}-\sqrt[3]{3x+2}=0 LaTeX formula: \sqrt{x+2}-\sqrt[3]{3x+2}=0](/uploads/formulas/d870c210d3ce205bd55044f320f6e63500f0a2e5.1.1.png) равносильной ему системой уравнений:
равносильной ему системой уравнений:
 , то второе уравнение системы примет вид:
, то второе уравнение системы примет вид: или
или  .
. Очевидно, что число
 является корнем этого уравнения.
является корнем этого уравнения. на двучлен
на двучлен  :
:
 или
или  ,
, откуда
 (этот корень уравнения был уже найден) и
(этот корень уравнения был уже найден) и  .
.  , то
, то  , откуда
, откуда 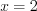 .
. Ответ:
 .
. , при котором уравнение
, при котором уравнение  имеет один корень.
имеет один корень. .
. Найдем корни уравнения, решая совокупность уравнений:
1)
 , откуда
, откуда  ;
;2)
 , откуда
, откуда  .
. Поскольку согласно условию задачи уравнение имеет один корень (число
 ), то
), то  – посторонний корень (не принадлежит области допустимых значений уравнения).
– посторонний корень (не принадлежит области допустимых значений уравнения). Следовательно,
 , откуда
, откуда  .
. Ответ:
 .
.
