Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
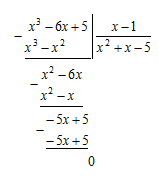
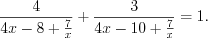
 ,
,  ,
,  (
( ),
),
 ,
,  , откуда
, откуда 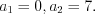
 , откуда
, откуда  , а так как
, а так как 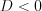 , то
, то  ;
; 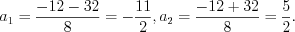
Рациональными называют уравнения вида  и
и 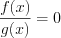 , где
, где  и
и  – многочлены.
– многочлены.
 и
и 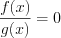 , где
, где  и
и  – многочлены.
– многочлены. Решение рациональных уравнений
1. Если уравнение имеет вид  , где
, где  – многочлен, степень которого выше второй, то, разложив его левую часть на множители, заменяют данное уравнение совокупностью уравнений, приравнивая каждый множитель к нулю.
– многочлен, степень которого выше второй, то, разложив его левую часть на множители, заменяют данное уравнение совокупностью уравнений, приравнивая каждый множитель к нулю.
 , где
, где  – многочлен, степень которого выше второй, то, разложив его левую часть на множители, заменяют данное уравнение совокупностью уравнений, приравнивая каждый множитель к нулю.
– многочлен, степень которого выше второй, то, разложив его левую часть на множители, заменяют данное уравнение совокупностью уравнений, приравнивая каждый множитель к нулю.2. Если уравнение имеет вид 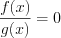 , то при
, то при 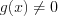 оно равносильно уравнению
оно равносильно уравнению 
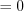 .
.
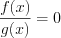 , то при
, то при 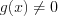 оно равносильно уравнению
оно равносильно уравнению 
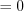 .
.3. Если уравнение имеет вид  , то при
, то при 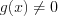 оно равносильно уравнению
оно равносильно уравнению  .
.
 , то при
, то при 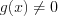 оно равносильно уравнению
оно равносильно уравнению  .
.4. Если уравнение имеет вид 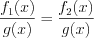 , то при
, то при 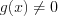 оно равносильно уравнению
оно равносильно уравнению 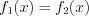 .
.
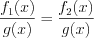 , то при
, то при 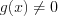 оно равносильно уравнению
оно равносильно уравнению 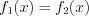 .
.5. Если уравнение имеет вид 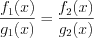 , то при
, то при 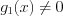 и
и 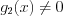 оно равносильно уравнению
оно равносильно уравнению 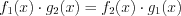 .
.
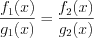 , то при
, то при 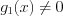 и
и 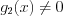 оно равносильно уравнению
оно равносильно уравнению 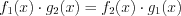 .
.6. Метод подстановки.
7. Рассмотрим метод решения одного из видов симметрических уравнений.
Н а п р и м е р, уравнение имеет вид: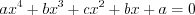 , (5.10)
, (5.10)
Разделим обе его части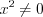 и введем подстановку
и введем подстановку 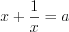 . (5.10.1)
. (5.10.1)
Н а п р и м е р, уравнение имеет вид:
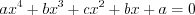 , (5.10)
, (5.10) Разделим обе его части
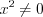 и введем подстановку
и введем подстановку 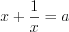 . (5.10.1)
. (5.10.1)Решение систем рациональных уравнений
Решая системы рациональных уравнений, можно:
1) выражать переменную из одного уравнения и подставлять ее значение в другое уравнение системы;
2) складывать и вычитать уравнения системы;
3) делить и умножать уравнения системы;
4) вводить подстановку.
Пример 1. Найдите произведение всех действительных корней уравнения 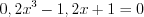 .
.
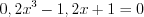 .
.Решение. Запишем уравнение в виде 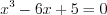 .
.
Если уравнение имеет целые корни, то эти корни найдем среди делителей свободного члена.
Запишем делители числа : это числа
: это числа  и
и  .
.
Подберем корень уравнения:
если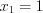 , то
, то  , следовательно, число
, следовательно, число  – корень этого уравнения.
– корень этого уравнения.
Разделим обе части уравнения на двучлен :
:
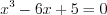 .
. Если уравнение имеет целые корни, то эти корни найдем среди делителей свободного члена.
Запишем делители числа
 : это числа
: это числа  и
и  .
. Подберем корень уравнения:
если
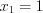 , то
, то  , следовательно, число
, следовательно, число  – корень этого уравнения.
– корень этого уравнения. Разделим обе части уравнения на двучлен
 :
: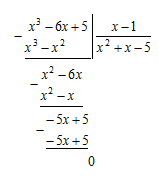
Решим уравнение 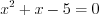 .
.
Так как дискриминант уравнения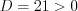 , то это уравнение имеет два корня, произведение которых равно
, то это уравнение имеет два корня, произведение которых равно 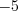 .
.
Найдем произведение всех корней уравнения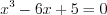 :
:
 .
.
Ответ: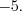
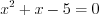 .
. Так как дискриминант уравнения
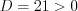 , то это уравнение имеет два корня, произведение которых равно
, то это уравнение имеет два корня, произведение которых равно 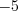 .
. Найдем произведение всех корней уравнения
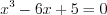 :
:  .
. Ответ:
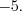
Пример 2. Найдите сумму всех корней уравнения 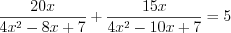 .
.
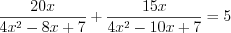 .
. Решение. Так как число нуль не является корнем этого уравнения, то выполним следующее преобразование:
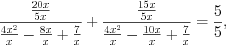
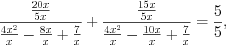
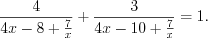
В результате подстановки 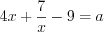 уравнение примет вид:
уравнение примет вид:
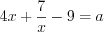 уравнение примет вид:
уравнение примет вид: ,
,  ,
,  (
( ),
),  ,
,  , откуда
, откуда 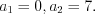
Учитывая подстановку, решим два уравнения:
 , откуда
, откуда  , а так как
, а так как 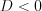 , то
, то  ;
; 2)  , откуда
, откуда  , а так как
, а так как 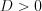 , то
, то  .
.
Ответ: .
.
 , откуда
, откуда  , а так как
, а так как 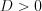 , то
, то  .
. Ответ:
 .
.Пример 3. Решите уравнение 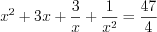 .
.
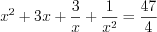 .
.Запишем уравнение в виде:
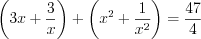 или
или 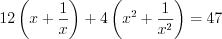 .
.
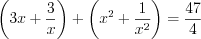 или
или 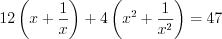 .
.Преобразуем выражение 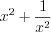 :
:
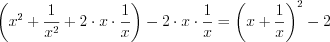 .
.
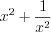 :
: 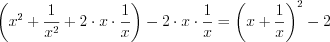 .
.Полагая 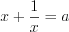 и
и 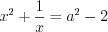 , получим:
, получим:
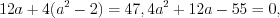 откуда
откуда
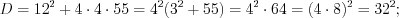
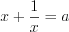 и
и 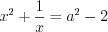 , получим:
, получим: 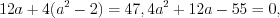 откуда
откуда 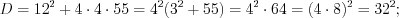
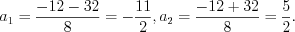
Учитывая подстановку, решим уравнения:
1)  или
или  , откуда
, откуда 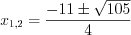 ;
;
 или
или  , откуда
, откуда 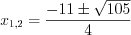 ;
;2)  или
или 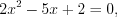 откуда
откуда 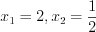 .
.
 или
или 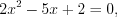 откуда
откуда 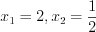 .
.Ответ: 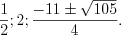
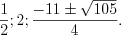
Пример 4. Решите систему уравнений 

Решение. Полагая  запишем данную систему уравнений в виде:
запишем данную систему уравнений в виде:
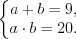
 запишем данную систему уравнений в виде:
запишем данную систему уравнений в виде: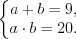
Заметим, что решением полученной системы уравнений являются пары чисел
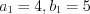 и
и  .
.
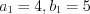 и
и  .
.Учитывая подстановку, решим две системы уравнений:
1) 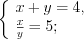
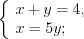

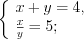
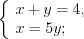

2) 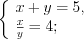
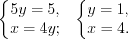
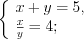
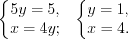
Ответ: 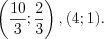
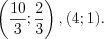
Пример 5. Решите систему уравнений 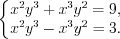
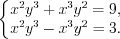
Решение. Систему уравнений запишем в виде:
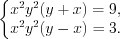
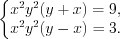
Разделим первое уравнение системы на второе:
 , откуда
, откуда  .
.
 , откуда
, откуда  .
.По основному свойству пропорции получим:
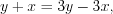 откуда
откуда 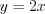 .
.
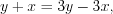 откуда
откуда 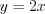 .
.Подставим значение 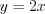 в первое уравнение системы и найдем значение переменной
в первое уравнение системы и найдем значение переменной  :
:
 ,
,  ,
,  , откуда
, откуда ![x=\sqrt[5]{0,75}. LaTeX formula: x=\sqrt[5]{0,75}.](/uploads/formulas/6e8035c29f2727c20f8c8196e983e62be1c5ad36.1.1.png)
Найдем значение переменной :
:
![y=2x, y=2\sqrt[5]{0,75}. LaTeX formula: y=2x, y=2\sqrt[5]{0,75}.](/uploads/formulas/d15be08ebdcb34b9f27436f473d362ee350f7808.1.1.png)
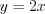 в первое уравнение системы и найдем значение переменной
в первое уравнение системы и найдем значение переменной  :
:  ,
,  ,
,  , откуда
, откуда ![x=\sqrt[5]{0,75}. LaTeX formula: x=\sqrt[5]{0,75}.](/uploads/formulas/6e8035c29f2727c20f8c8196e983e62be1c5ad36.1.1.png)
Найдем значение переменной
 :
: ![y=2x, y=2\sqrt[5]{0,75}. LaTeX formula: y=2x, y=2\sqrt[5]{0,75}.](/uploads/formulas/d15be08ebdcb34b9f27436f473d362ee350f7808.1.1.png)
Ответ: ![(\sqrt[5]{0,75};2\sqrt[5]{0,75}) LaTeX formula: (\sqrt[5]{0,75};2\sqrt[5]{0,75})](/uploads/formulas/7a88a97f9ef8b1d3a880794d8c3bc6f6d6b13f57.1.1.png) .
.
![(\sqrt[5]{0,75};2\sqrt[5]{0,75}) LaTeX formula: (\sqrt[5]{0,75};2\sqrt[5]{0,75})](/uploads/formulas/7a88a97f9ef8b1d3a880794d8c3bc6f6d6b13f57.1.1.png) .
.1. Линейные и квадратные уравнения являются рациональными.
2. Решая дробно-рациональные уравнения, необходимо учитывать область определения уравнения.
3. Система уравнений симметричная, если в результате замены переменной  на переменную
на переменную  , а переменной
, а переменной  на переменную
на переменную  , получаем ту же систему. Если
, получаем ту же систему. Если  – решение этой системы, то и
– решение этой системы, то и 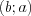 также решение системы.
также решение системы.
 на переменную
на переменную  , а переменной
, а переменной  на переменную
на переменную  , получаем ту же систему. Если
, получаем ту же систему. Если  – решение этой системы, то и
– решение этой системы, то и 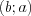 также решение системы.
также решение системы.
