Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
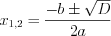 . (5.6)
. (5.6)
Квадратным называют уравнение вида  при условии, что
при условии, что  .
.
Числа
 и
и  называют коэффициентами уравнения.
называют коэффициентами уравнения.
Число считают старшим коэффициентом, а число
считают старшим коэффициентом, а число  – свободным членом уравнения.
– свободным членом уравнения.
 при условии, что
при условии, что  .
. Числа

 и
и  называют коэффициентами уравнения.
называют коэффициентами уравнения. Число
 считают старшим коэффициентом, а число
считают старшим коэффициентом, а число  – свободным членом уравнения.
– свободным членом уравнения. Если коэффициенты уравнения  и (или)
и (или)  равны нулю, то имеем неполные квадратные уравнения:
равны нулю, то имеем неполные квадратные уравнения:
1) ;
;
2) ;
;
3)
 и (или)
и (или)  равны нулю, то имеем неполные квадратные уравнения:
равны нулю, то имеем неполные квадратные уравнения: 1)
 ;
; 2)
 ;
; 3)

Решение неполных
квадратных уравнений
1. Если уравнение имеет вид  , то
, то
 и
и  (двукратный корень).
(двукратный корень).
 , то
, то  и
и  (двукратный корень).
(двукратный корень). 2. Если уравнение имеет вид  ,
,
то ,
,  и
и  , при условии, что
, при условии, что  .
.
Например, уравнение решений не имеет, так как
решений не имеет, так как  .
.
 ,
, то
 ,
,  и
и  , при условии, что
, при условии, что  .
. Например, уравнение
 решений не имеет, так как
решений не имеет, так как  .
.2. Если уравнение имеет вид  , то
, то
 , откуда
, откуда  или
или  .
.
Следовательно, данное уравнение имеет два действительных корня:
 и
и  .
.
Например, решим уравнение откуда
откуда 
 , то
, то  , откуда
, откуда  или
или  .
. Следовательно, данное уравнение имеет два действительных корня:
 и
и  .
. Например, решим уравнение
 откуда
откуда 
Решение полных квадратных уравнений
Рассмотрим решение квадратного уравнения
 , (5.4)
, (5.4)
при условии, что ни один из его коэффициентов не равен нулю.
1. Если 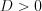 , то уравнение имеет два различных действительных корня, определяемые по формуле:
, то уравнение имеет два различных действительных корня, определяемые по формуле:
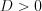 , то уравнение имеет два различных действительных корня, определяемые по формуле:
, то уравнение имеет два различных действительных корня, определяемые по формуле: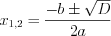 . (5.6)
. (5.6)2. Если 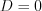 , то
, то  (двукратный корень).
(двукратный корень).
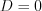 , то
, то  (двукратный корень).
(двукратный корень).3. Если 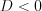 , то уравнение не имеет действительных корней.
, то уравнение не имеет действительных корней.
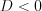 , то уравнение не имеет действительных корней.
, то уравнение не имеет действительных корней.Теорема Виета. Сумма корней квадратного уравнения  равна
равна 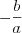 , а произведение его корней равно
, а произведение его корней равно  . (при условии, что
. (при условии, что 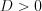 ).
).
Если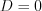 , то учитываем, что
, то учитываем, что  – двукратный корень уравнения.
– двукратный корень уравнения.
 равна
равна 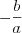 , а произведение его корней равно
, а произведение его корней равно  . (при условии, что
. (при условии, что 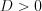 ).
). Если
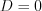 , то учитываем, что
, то учитываем, что  – двукратный корень уравнения.
– двукратный корень уравнения. Н а п р и м е р, рассмотрим уравнение  .
.
Так как , то по теореме Виета:
, то по теореме Виета:  , а
, а  .
.
 .
. Так как
 , то по теореме Виета:
, то по теореме Виета:  , а
, а  .
.Приведенным квадратным уравнением называют уравнение вида:
 . (5.7)
. (5.7)
Согласно теореме Виета сумма корней уравнения 5.7 равна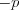 , а произведение его корней равно
, а произведение его корней равно  .
.
 . (5.7)
. (5.7) Согласно теореме Виета сумма корней уравнения 5.7 равна
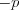 , а произведение его корней равно
, а произведение его корней равно  .
. Н а п р и м е р, рассмотрим уравнение  . Так как
. Так как 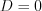 , то:
, то:  , а
, а  .
.
 . Так как
. Так как 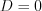 , то:
, то:  , а
, а  .
.Теорема,обратная теореме Виета. Числа  и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения  , где
, где  , если их сумма равна
, если их сумма равна 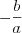 , а произведение равно
, а произведение равно  .
.
 и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения  , где
, где  , если их сумма равна
, если их сумма равна 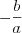 , а произведение равно
, а произведение равно  .
.Разложение квадратного трехчлена на множители
Квадратный трехчлен  можно разложить на линейные множители по формуле:
можно разложить на линейные множители по формуле:
 (5.8)
(5.8)
где и
и  – корни этого трехчлена.
– корни этого трехчлена.
 можно разложить на линейные множители по формуле:
можно разложить на линейные множители по формуле:  (5.8)
(5.8) где
 и
и  – корни этого трехчлена.
– корни этого трехчлена.Биквадратные уравнения
Биквадратным уравнением называют уравнение вида:
 , (5.9)
, (5.9)
где и
и  – действительные числа и
– действительные числа и  .
.
С помощью подстановки это уравнение сводится к квадратному уравнению
это уравнение сводится к квадратному уравнению
 .
.
 , (5.9)
, (5.9) где
 и
и  – действительные числа и
– действительные числа и  .
. С помощью подстановки
 это уравнение сводится к квадратному уравнению
это уравнение сводится к квадратному уравнению  .
. Пример 1. Разложите на множители квадратный трехчлен  .
.
 .
. Решение. Решим квадратное уравнение  .
.
 .
. Пример 2. Решите уравнение  .
.
 .
. Тогда:  ,
,  ,
,  ,
, 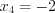 .
.
 ,
,  ,
,  ,
, 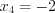 .
.Ответ: 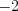 ;
;  ;
;  ;
;  .
.
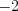 ;
;  ;
;  ;
;  .
.Пример 3. Составьте квадратное уравнение с корнями  и
и  , где
, где  и
и  – корни уравнения
– корни уравнения  .
.
 и
и  , где
, где  и
и  – корни уравнения
– корни уравнения  .
.Решение. Рассмотрим уравнение  .
.
 .
.По теореме Виета запишем:  и
и  .
.
 и
и  .
.Найдем коэффициенты  и
и  , учитывая, что
, учитывая, что  и
и  :
:
 и
и  , учитывая, что
, учитывая, что  и
и  :
: 1)  ;
;
 ;
;2)  .
.
 .
.Подставим значения  и
и  в уравнение
в уравнение  и получим:
и получим:
 или
или  .
.
Ответ: .
.
 и
и  в уравнение
в уравнение  и получим:
и получим: или
или  .
. Ответ:
 .
.Пример 4. Составьте квадратное уравнение с рациональными коэффициентами, один из корней которого равен  .
.
 .
.Решение. Согласно условию задачи:
 , или
, или  , или
, или  . Тогда
. Тогда  .
.
 , или
, или  , или
, или  . Тогда
. Тогда  .
.Запишем искомое уравнение:  .
.
Ответ: .
.
 .
. Ответ:
 .
.Прежде, чем находить сумму и произведение корней квадратного уравнения по теореме Виета, необходимо убедиться в том, что это уравнение имеет действительные корни, т. е. его дискриминант не отрицателен.
Н а п р и м е р, нельзя записать, что сумма корней квадратного уравнения  равна
равна  , а произведение его корней равно
, а произведение его корней равно  , так как дискриминант этого уравнения отрицательный, следовательно, оно вовсе не имеет действительных корней.
, так как дискриминант этого уравнения отрицательный, следовательно, оно вовсе не имеет действительных корней.
 равна
равна  , а произведение его корней равно
, а произведение его корней равно  , так как дискриминант этого уравнения отрицательный, следовательно, оно вовсе не имеет действительных корней.
, так как дискриминант этого уравнения отрицательный, следовательно, оно вовсе не имеет действительных корней.






 .
.










