Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 , если
, если ![x\in [-1;1] LaTeX formula: x\in [-1;1]](/uploads/formulas/8dc88849028ecc07f6fd9cd49c35c436712b3757.1.1.png) ; (4.35)
; (4.35) , если
, если ![x\in [-1;1] LaTeX formula: x\in [-1;1]](https://helpy.quali.me/uploads/formulas/8dc88849028ecc07f6fd9cd49c35c436712b3757.1.1.png) ; (4.36)
; (4.36) , если
, если  ; (4.37)
; (4.37) , если
, если  ; (4.38)
; (4.38) , если
, если ![x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ] LaTeX formula: x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](/uploads/formulas/9ceaa53e548e6ee04d518282f14a2ca80511829d.1.1.png) ; (4.39)
; (4.39) , если
, если ![x\in [0;\pi] LaTeX formula: x\in [0;\pi]](https://helpy.quali.me/uploads/formulas/cda754f516a055745d150991b167878543c5fac3.1.1.png) ; (4.40)
; (4.40) , если
, если  ; (4.41)
; (4.41) , если
, если  . (4.42)
. (4.42) ; (4.43)
; (4.43) ; (4.44)
; (4.44) ; (4.45)
; (4.45) . (4.46)
. (4.46)
 ,
,  .
.
Введем подстановку: , откуда
, откуда  .
. , откуда
, откуда  ,
,  ,
,  .
.
Арксинусом числа ![a\in [-1;1] LaTeX formula: a\in [-1;1]](/uploads/formulas/94b758373b401fdce65da979c0c9421155b87c67.1.1.png) называют такое число
называют такое число ![x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ] LaTeX formula: x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](https://helpy.quali.me/uploads/formulas/9ceaa53e548e6ee04d518282f14a2ca80511829d.1.1.png) , синус которого равен
, синус которого равен  , т. е. если
, т. е. если  , то
, то  .
.
![a\in [-1;1] LaTeX formula: a\in [-1;1]](/uploads/formulas/94b758373b401fdce65da979c0c9421155b87c67.1.1.png) называют такое число
называют такое число ![x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ] LaTeX formula: x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](https://helpy.quali.me/uploads/formulas/9ceaa53e548e6ee04d518282f14a2ca80511829d.1.1.png) , синус которого равен
, синус которого равен  , т. е. если
, т. е. если  , то
, то  .
.Арккосинусом числа ![a\in [-1;1] LaTeX formula: a\in [-1;1]](https://helpy.quali.me/uploads/formulas/94b758373b401fdce65da979c0c9421155b87c67.1.1.png) называют такое число
называют такое число ![x\in [0;\pi] LaTeX formula: x\in [0;\pi]](/uploads/formulas/cda754f516a055745d150991b167878543c5fac3.1.1.png) , косинус которого равен
, косинус которого равен  , т. е. если
, т. е. если  ,
,  .
.
![a\in [-1;1] LaTeX formula: a\in [-1;1]](https://helpy.quali.me/uploads/formulas/94b758373b401fdce65da979c0c9421155b87c67.1.1.png) называют такое число
называют такое число ![x\in [0;\pi] LaTeX formula: x\in [0;\pi]](/uploads/formulas/cda754f516a055745d150991b167878543c5fac3.1.1.png) , косинус которого равен
, косинус которого равен  , т. е. если
, т. е. если  ,
,  .
.Арктангенсом числа  называют такое число
называют такое число  , тангенс которого равен
, тангенс которого равен  , т. е. если
, т. е. если  , то
, то  .
.
 называют такое число
называют такое число  , тангенс которого равен
, тангенс которого равен  , т. е. если
, т. е. если  , то
, то  .
.Арккотангенсом числа  называют такое число
называют такое число  , котангенс которого равен
, котангенс которого равен  , т. е. если
, т. е. если  , то
, то  .
.
 называют такое число
называют такое число  , котангенс которого равен
, котангенс которого равен  , т. е. если
, т. е. если  , то
, то  .
. Н а п р и м е р:
1) , так как
, так как ![\frac{\sqrt{3}}{2}\in [-1;1] LaTeX formula: \frac{\sqrt{3}}{2}\in [-1;1]](/uploads/formulas/6a8d5f213a63e027ed249362a640e5b3f47cc6f8.1.1.png) и
и  ;
;
1)
 , так как
, так как ![\frac{\sqrt{3}}{2}\in [-1;1] LaTeX formula: \frac{\sqrt{3}}{2}\in [-1;1]](/uploads/formulas/6a8d5f213a63e027ed249362a640e5b3f47cc6f8.1.1.png) и
и  ;
;2)  не определен, так как
не определен, так как ![1,1\notin }[-1;1] LaTeX formula: 1,1\notin }[-1;1]](/uploads/formulas/a37ed0f2b4963d536ad123e40493c060fe61d252.1.1.png) .
.
 не определен, так как
не определен, так как ![1,1\notin }[-1;1] LaTeX formula: 1,1\notin }[-1;1]](/uploads/formulas/a37ed0f2b4963d536ad123e40493c060fe61d252.1.1.png) .
.Справедливы равенства:
 , если
, если ![x\in [-1;1] LaTeX formula: x\in [-1;1]](/uploads/formulas/8dc88849028ecc07f6fd9cd49c35c436712b3757.1.1.png) ; (4.35)
; (4.35) , если
, если ![x\in [-1;1] LaTeX formula: x\in [-1;1]](https://helpy.quali.me/uploads/formulas/8dc88849028ecc07f6fd9cd49c35c436712b3757.1.1.png) ; (4.36)
; (4.36) , если
, если  ; (4.37)
; (4.37) , если
, если  ; (4.38)
; (4.38) , если
, если ![x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ] LaTeX formula: x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](/uploads/formulas/9ceaa53e548e6ee04d518282f14a2ca80511829d.1.1.png) ; (4.39)
; (4.39) , если
, если ![x\in [0;\pi] LaTeX formula: x\in [0;\pi]](https://helpy.quali.me/uploads/formulas/cda754f516a055745d150991b167878543c5fac3.1.1.png) ; (4.40)
; (4.40) , если
, если  ; (4.41)
; (4.41) , если
, если  . (4.42)
. (4.42)Преобразования функций отрицательного аргумента
 ; (4.43)
; (4.43) ; (4.44)
; (4.44) ; (4.45)
; (4.45) . (4.46)
. (4.46) ,
,  .
. Введем подстановку:
 , откуда
, откуда  .
.Тогда по формуле приведения:  .
.
 .
.Найдем  , зная
, зная  .
.
Согласно формуле , получим:
, получим:
 , зная
, зная  .
. Согласно формуле
 , получим:
, получим:  , откуда
, откуда  ,
,  ,
,  .
. Так как  , то
, то  .
.
Ответ: .
.
 , то
, то  .
. Ответ:
 .
.Пример 2. Найдите значение выражения  .
.
 .
.Решение. Учитывая основной период функции 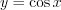 и область определения функции
и область определения функции  , по формуле 4.40 получим:
, по формуле 4.40 получим:
 ,
,
 ,
,
 .
.
Ответ: .
.
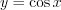 и область определения функции
и область определения функции  , по формуле 4.40 получим:
, по формуле 4.40 получим:  ,
,  ,
,  .
. Ответ:
 .
.Применяя равенства  и
и  , следите за тем, чтобы значение переменной
, следите за тем, чтобы значение переменной  удовлетворяло требованиям:
удовлетворяло требованиям: ![x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ] LaTeX formula: x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](https://helpy.quali.me/uploads/formulas/9ceaa53e548e6ee04d518282f14a2ca80511829d.1.1.png) в первом случае и
в первом случае и ![x\in [0;\pi] LaTeX formula: x\in [0;\pi]](https://helpy.quali.me/uploads/formulas/cda754f516a055745d150991b167878543c5fac3.1.1.png) во втором случае.
во втором случае.
 и
и  , следите за тем, чтобы значение переменной
, следите за тем, чтобы значение переменной  удовлетворяло требованиям:
удовлетворяло требованиям: ![x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ] LaTeX formula: x\in \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]](https://helpy.quali.me/uploads/formulas/9ceaa53e548e6ee04d518282f14a2ca80511829d.1.1.png) в первом случае и
в первом случае и ![x\in [0;\pi] LaTeX formula: x\in [0;\pi]](https://helpy.quali.me/uploads/formulas/cda754f516a055745d150991b167878543c5fac3.1.1.png) во втором случае.
во втором случае.







