Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
; (4.2)
; (4.3)
; (4.4)
; (4.5)
. (4.6)
; (4.7)
; (4.8)
; (4.9)
; (4.10)
; (4.11)
. (4.12)
; (4.13)
. (4.14)
; (4.15)
. (4.16)
; (4.17)
; (4.18)
; (4.19)
; (4.20)
; (4.21)
. (4.22)
; (4.23)
; (4.24)
. (4.25)
; (4.26)
; (4.27) 
. (4.28) 
; (4.29)
; (4.31)
; (4.30)
. (4.32)
и 
.
; 
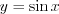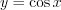или 
; 
;
; или ; 
;
; 
или 
; 
;
. или . 
.
Основные тригонометрические тождества
К основным тригонометрическим тождествам относят формулы, устанавливающие связь между тригонометрическими функциями одного и того же аргумента:
; (4.1)
; (4.1); (4.2); (4.3); (4.4); (4.5). (4.6)Формула 4.1 справедлива при любых значениях х. Формулы 4.2, 4.3, 4.4, 4.5, 4.6 верны только при тех значениях аргумента, для которых функция тангенс и котангенс определены.
Формулы сложения
Формулы 4.7 – 4.12 позволяют представить тригонометрическую функцию суммы и разности двух аргументов через функции этих аргументов или найти тригонометрическую функцию суммы и разности двух аргументов, зная значения функций каждого аргумента.
; (4.7); (4.8); (4.9); (4.10); (4.11). (4.12)Формулы 4.7, 4.8, 4.9, 4.10 справедливы при любых значениях х и у. Формулы 4.11 и 4.12 верны только при тех значениях аргумента, для которых функция тангенс определена.
Формулы двойного аргумента
Формулы 4.13 и 4.14 позволяют уменьшить или увеличить аргумент тригонометрической функции в два раза.
; (4.13). (4.14)Формулы понижения степени
Формулы 4.15 и 4.16 позволяют понизить степень функций косинус и синус. Часто эти формулы называют формулами половинного аргумента.
; (4.15). (4.16)Формулы преобразования суммы в произведение
; (4.17); (4.18); (4.19); (4.20); (4.21). (4.22)Формулы 4.21 и 4.22 верны только при тех значениях аргумента, для которых функция тангенс определена.
Формулы преобразования произведения в сумму
; (4.23); (4.24). (4.25)Универсальная тригонометрическая подстановка
; (4.26); (4.27) . (4.28) Формулы 4.26, 4.27, 4.28 позволяют выразить функции синус, косинус и тангенс некоторого аргумента через тангенс половинного аргумента. Формулы 4.26, 4.27, 4.28 верны только при тех значениях аргумента, для которых функция тангенс определена.
Преобразование функций отрицательных аргументов
Преобразования отрицательных аргументов тригонометрических функций основано на том, что функция косинус является четной, а функции синус, тангенс и котангенс являются нечетными.
; (4.29); (4.31); (4.30). (4.32)Пример 1. Преобразуйте в произведение сумму 
.
.Решение. Запишем выражение в виде:
.
. 
, 
,
,
.
, 
,
. Ответ: 
.
.Пример 2. Вычислите 
, если 
.
, если .Решение. Вычтем из аргумента функции косинус ее два основных периода и применим формулу 4.10:
, 
,
, 
,
.
Так как
, а , то 
.
, , , , . Так как
, а , то . и .Тогда, 
.
Ответ:
.
. Ответ:
.Пример 3. Вычислите 
, если 
.
, если .
Подставляя значения 
и 
в выражение 
, получим:
.
Ответ:
.
и в выражение , получим: . Ответ:
.Пример 4. Найдите 
, если 
, 
и 
, 
.
, если , и , .
, откуда 
Так как и , то при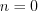 
получим: 
.
и , то при 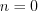получим: .Ответ: 
.
.Выполняя преобразования и вычисления тригонометрических выражений необходимо помнить, что целое количество основных периодов функции можно вычитать из аргумента функции или прибавлять к ее аргументу:
ФУНКЦИЯ ОСНОВНОЙ ПЕРИОД ФОРМУЛА ( 
)
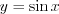); или ; ;; или ; ;; 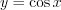или ; ;. или . .