Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты

Натуральными числами называют числа, с помощью которых определяется количество предметов того или иного множества.
Ряд натуральных чисел бесконечен: ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , …
, …
Множество всех натуральных чисел обозначают .
.
Любое натуральное число можно записать с помощью десяти цифр:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Цифры ,
,  ,
,  ,
,  ,
,  называют четными, а цифры
называют четными, а цифры  ,
,  ,
,  ,
,  ,
,  – нечетными.
– нечетными.
Ряд натуральных чисел бесконечен:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , …
, … Множество всех натуральных чисел обозначают
 .
. Любое натуральное число можно записать с помощью десяти цифр:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. Цифры
 ,
,  ,
,  ,
,  ,
,  называют четными, а цифры
называют четными, а цифры  ,
,  ,
,  ,
,  ,
,  – нечетными.
– нечетными. Числа, запись которых оканчивается четной цифрой, называют четными числами.
Числа, запись которых оканчивается нечетной цифрой, называют нечетными числами.
Н а п р и м е р, натуральные числа ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 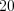 , … – четные,
, … – четные,
а натуральные числа ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , … – нечетные.
, … – нечетные.
Числа, запись которых оканчивается нечетной цифрой, называют нечетными числами.
Н а п р и м е р, натуральные числа
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 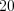 , … – четные,
, … – четные, а натуральные числа
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , … – нечетные.
, … – нечетные.Четные числа записывают в виде  , где
, где  – любое натуральное число.
– любое натуральное число.
Нечетные числа записывают в виде , если
, если  – любое натуральное число, или в виде
– любое натуральное число, или в виде  , если
, если  – любое натуральное число и число
– любое натуральное число и число  .
.
 , где
, где  – любое натуральное число.
– любое натуральное число. Нечетные числа записывают в виде
 , если
, если  – любое натуральное число, или в виде
– любое натуральное число, или в виде  , если
, если  – любое натуральное число и число
– любое натуральное число и число  .
.Над натуральными числами можно производить арифметические действия:
1) сложение: , где
, где  и
и  – слагаемые,
– слагаемые,  – сумма;
– сумма;
2) вычитание: , где
, где  – уменьшаемое,
– уменьшаемое,  – вычитаемое,
– вычитаемое,  – разность;
– разность;
3) умножение: , где
, где  и
и  – множители,
– множители,  – произведение;
– произведение;
4) деление: , где
, где  – делимое,
– делимое,  – делитель,
– делитель,  – частное.
– частное.
1) сложение:
 , где
, где  и
и  – слагаемые,
– слагаемые,  – сумма;
– сумма; 2) вычитание:
 , где
, где  – уменьшаемое,
– уменьшаемое,  – вычитаемое,
– вычитаемое,  – разность;
– разность; 3) умножение:
 , где
, где  и
и  – множители,
– множители,  – произведение;
– произведение; 4) деление:
 , где
, где  – делимое,
– делимое,  – делитель,
– делитель,  – частное.
– частное.Чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, необходимо частное умножить на делитель.
Чтобы найти неизвестный делитель, необходимо делимое разделить на частное.
Чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, необходимо частное умножить на делитель.
Чтобы найти неизвестный делитель, необходимо делимое разделить на частное.
Законы сложения
1. Переместительный: от перестановки слагаемых значение суммы не изменится:
 .
.
Н а п р и м е р, .
.
2. Сочетательный: чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего:
 .
.
Н а п р и м е р, .
.
1. Переместительный: от перестановки слагаемых значение суммы не изменится:
 .
. Н а п р и м е р,
 .
. 2. Сочетательный: чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего:
 .
. Н а п р и м е р,
 .
.Законы умножения
1. Переместительный: от перестановки множителей значение произведения не изменится:
 .
.
2. Сочетательный: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего:
 .
.
3. Распределительный относительно сложения: чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные произведения сложить:
 .
.
4. Распределительный относительно вычитания: чтобы умножить разность на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе:
 .
.
Н а п р и м е р:
1) ;
;
2) ;
;
3) ;
;
4) .
.
1. Переместительный: от перестановки множителей значение произведения не изменится:
 .
. 2. Сочетательный: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего:
 .
. 3. Распределительный относительно сложения: чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные произведения сложить:
 .
. 4. Распределительный относительно вычитания: чтобы умножить разность на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе:
 .
. Н а п р и м е р:
1)
 ;
; 2)
 ;
; 3)
 ;
;4)
 .
.Делимость натуральных чисел
Если натуральное число  делится без остатка на натуральное число
делится без остатка на натуральное число  , то число
, то число  называют кратным числа
называют кратным числа  , а число
, а число  – делителем числа
– делителем числа  .
.
Н а п р и м е р, . Число
. Число  кратно числу
кратно числу  , а число
, а число  является делителем числа
является делителем числа  .
.
 делится без остатка на натуральное число
делится без остатка на натуральное число  , то число
, то число  называют кратным числа
называют кратным числа  , а число
, а число  – делителем числа
– делителем числа  .
. Н а п р и м е р,
 . Число
. Число  кратно числу
кратно числу  , а число
, а число  является делителем числа
является делителем числа  .
. Если число  кратно числу
кратно числу  , то записывают:
, то записывают:  .
.
 кратно числу
кратно числу  , то записывают:
, то записывают:  .
.Признаки делимости натуральных чисел
1. Число делится на  , если его запись оканчивается четной цифрой.
, если его запись оканчивается четной цифрой.
Н а п р и м е р, числа ,
,  и
и  делятся на
делятся на  .
.
 , если его запись оканчивается четной цифрой.
, если его запись оканчивается четной цифрой. Н а п р и м е р, числа
 ,
,  и
и  делятся на
делятся на  .
.2. Число делится на  , если сумма цифр числа делится на
, если сумма цифр числа делится на  .
.
Н а п р и м е р, делится на
делится на  , так как сумма цифр этого числа
, так как сумма цифр этого числа  и число
и число  делится на
делится на  .
.
 , если сумма цифр числа делится на
, если сумма цифр числа делится на  .
. Н а п р и м е р,
 делится на
делится на  , так как сумма цифр этого числа
, так как сумма цифр этого числа  и число
и число  делится на
делится на  .
.3. Число делится на  , если его запись оканчивается цифрой
, если его запись оканчивается цифрой  или цифрой
или цифрой  .
.
Н а п р и м е р, числа и
и  делятся на
делятся на  .
.
 , если его запись оканчивается цифрой
, если его запись оканчивается цифрой  или цифрой
или цифрой  .
. Н а п р и м е р, числа
 и
и  делятся на
делятся на  .
.4. Число делится на  , если сумма цифр числа делится на
, если сумма цифр числа делится на  .
.
Н а п р и м е р, число делится на
делится на  , так как сумма цифр этого числа
, так как сумма цифр этого числа  делится на
делится на  .
.
 , если сумма цифр числа делится на
, если сумма цифр числа делится на  .
. Н а п р и м е р, число
 делится на
делится на  , так как сумма цифр этого числа
, так как сумма цифр этого числа  делится на
делится на  .
.5. Число делится на  , если его запись оканчивается цифрой
, если его запись оканчивается цифрой  .
.
Н а п р и м е р, число делится на
делится на  .
.
 , если его запись оканчивается цифрой
, если его запись оканчивается цифрой  .
. Н а п р и м е р, число
 делится на
делится на  .
. 6. Число делится на  , если две последние цифры его записи образуют число, которое делится на
, если две последние цифры его записи образуют число, которое делится на  .
.
Н а п р и м е р, число делится на
делится на  , так как число
, так как число 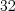 делится на
делится на  .
.
 , если две последние цифры его записи образуют число, которое делится на
, если две последние цифры его записи образуют число, которое делится на  .
.Н а п р и м е р, число
 делится на
делится на  , так как число
, так как число 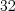 делится на
делится на  .
.7. Число делится на  , если три последние цифры его записи образуют число, которое делится на
, если три последние цифры его записи образуют число, которое делится на  .
.
Н а п р и м е р, число делится на
делится на  , так как число
, так как число  делится на
делится на  .
.
 , если три последние цифры его записи образуют число, которое делится на
, если три последние цифры его записи образуют число, которое делится на  .
.Н а п р и м е р, число
 делится на
делится на  , так как число
, так как число  делится на
делится на  .
.8. Число делится на  , если разность сумм цифр, стоящих на четных и нечетных местах, делится на
, если разность сумм цифр, стоящих на четных и нечетных местах, делится на  .
.
Н а п р и м е р, число делится на
делится на  , так как
, так как  и число
и число  делится на
делится на  .
.
 , если разность сумм цифр, стоящих на четных и нечетных местах, делится на
, если разность сумм цифр, стоящих на четных и нечетных местах, делится на  .
.Н а п р и м е р, число
 делится на
делится на  , так как
, так как  и число
и число  делится на
делится на  .
.9. Число делится на  , если две последние цифры его записи образуют число, которое делится на
, если две последние цифры его записи образуют число, которое делится на  .
.
Н а п р и м е р, числа ,
,  ,
,  и
и  делятся на
делятся на  .
.
 , если две последние цифры его записи образуют число, которое делится на
, если две последние цифры его записи образуют число, которое делится на  .
.Н а п р и м е р, числа
 ,
,  ,
,  и
и  делятся на
делятся на  .
. Деление с остатком
Разделить натуральное число  на натуральное число
на натуральное число  с остатком – значит представить число
с остатком – значит представить число  в виде
в виде  , где
, где  – неполное частное, а
– неполное частное, а  – остаток от деления
– остаток от деления  на
на  и
и  меньше
меньше  .
.
 на натуральное число
на натуральное число  с остатком – значит представить число
с остатком – значит представить число  в виде
в виде  , где
, где  – неполное частное, а
– неполное частное, а  – остаток от деления
– остаток от деления  на
на  и
и  меньше
меньше  .
.Если остаток равен нулю, то число  делится нацело на число
делится нацело на число  .
.
Н а п р и м е р, при делении натуральных чисел на , будем получать один из остатков: или
, будем получать один из остатков: или  , или
, или  , или
, или  , или
, или  .
.
 делится нацело на число
делится нацело на число  .
. Н а п р и м е р, при делении натуральных чисел на
 , будем получать один из остатков: или
, будем получать один из остатков: или  , или
, или  , или
, или  , или
, или  .
.Простые и составные числа
Числа, которые имеют только два различных делителя (делятся только сами на себя и на число 1), называют простыми.
Н а п р и м е р, простыми являются числа ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , …. .
, …. .
Н а п р и м е р, простыми являются числа
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , …. .
, …. . Числа, которые имеют более двух различных делителей, называют составными.
Составные числа можно представить в виде произведения двух и более простых множителей.
Н а п р и м е р, число составное, так как
составное, так как  .
.
Составные числа можно представить в виде произведения двух и более простых множителей.
Н а п р и м е р, число
 составное, так как
составное, так как  .
. Натуральные числа называются взаимно простыми, если они не имеют общих делителей, за исключением числа  .
.
Н а п р и м е р, числа и
и  взаимно простые.
взаимно простые.
 .
. Н а п р и м е р, числа
 и
и  взаимно простые.
взаимно простые. Наибольший общий делитель и наименьшее общее кратное
Общим делителем нескольких чисел называют число, которое является делителем каждого из этих чисел. Среди всех общих делителей всегда имеется наибольший. Это число называется наибольшим общим делителем (НОД).
Н а п р и м е р, числа ,
,  ,
,  и
и  являются общими делителями чисел
являются общими делителями чисел  и
и 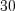 , а число
, а число  – их наибольший общий делитель;
– их наибольший общий делитель;
Н а п р и м е р, числа
 ,
,  ,
,  и
и  являются общими делителями чисел
являются общими делителями чисел  и
и 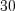 , а число
, а число  – их наибольший общий делитель;
– их наибольший общий делитель; Общим кратным нескольких чисел называют число, которое является кратным каждого из этих чисел. Среди всех общих кратных всегда есть наименьшее. Это число называется наименьшим общим кратным (НOК).
Н а п р и м е р, числа и
и  кратны числам
кратны числам  ,
,  ,
,  ,
,  и
и  , а число
, а число  – наименьшее общее кратное чисел
– наименьшее общее кратное чисел  и
и  .
.
Н а п р и м е р, числа
 и
и  кратны числам
кратны числам  ,
,  ,
,  ,
,  и
и  , а число
, а число  – наименьшее общее кратное чисел
– наименьшее общее кратное чисел  и
и  .
.Чтобы найти НОД нескольких чисел, необходимо разложить их на простые множители и найти произведение только тех множителей, которые имеются в разложениях всех чисел.
Чтобы найти НOК нескольких чисел, необходимо разложить их на простые множители, найти произведение всех множителей, входящих в разложение одного из чисел и недостающих множителей из разложений оставшихся чисел.
Пример 1. Найдите наибольший общий делитель и наименьшее общее кратное чисел  ,
,  и
и  .
.
Решение. Разложим эти числа на простые множители:
 ,
,  и
и  .
. Решение. Разложим эти числа на простые множители:

1. Найдем наибольший общий делитель чисел  ,
,  и
и  :
:
НОД .
.
2. Найдем наименьшее общее кратное чисел ,
,  и
и  :
:
НОК .
.
Ответ: и
и  .
.
 ,
,  и
и  :
: НОД
 .
. 2. Найдем наименьшее общее кратное чисел
 ,
,  и
и  :
: НОК
 .
. Ответ:
 и
и  .
.Пример 2. При делении пятизначного числа  на
на  в остатке получается
в остатке получается  . Найдите это число, если известно, что оно делится на
. Найдите это число, если известно, что оно делится на  .
.
Решение.
Согласно условию задачи число делится на
делится на  , следовательно, оно делится и на
, следовательно, оно делится и на  и на
и на  .
.
Если искомое число делится на , то число
, то число  делится на
делится на  .
.
Тогда может принимать одно из значений: или
может принимать одно из значений: или  , или
, или  , или
, или  .
.
Поскольку при делении числа на
на  в остатке получается
в остатке получается  , то
, то  .
.
Если же число делится на
делится на  , то сумма цифр этого числа делится на
, то сумма цифр этого числа делится на  , то есть
, то есть  .
.
Тогда при условии, что число будет делиться на
число будет делиться на  .
.
Запишем искомое число: .
.
Ответ: .
.
 на
на  в остатке получается
в остатке получается  . Найдите это число, если известно, что оно делится на
. Найдите это число, если известно, что оно делится на  .
. Решение.
Согласно условию задачи число
 делится на
делится на  , следовательно, оно делится и на
, следовательно, оно делится и на  и на
и на  .
.Если искомое число делится на
 , то число
, то число  делится на
делится на  .
. Тогда
 может принимать одно из значений: или
может принимать одно из значений: или  , или
, или  , или
, или  .
. Поскольку при делении числа
 на
на  в остатке получается
в остатке получается  , то
, то  .
. Если же число
 делится на
делится на  , то сумма цифр этого числа делится на
, то сумма цифр этого числа делится на  , то есть
, то есть  .
. Тогда при условии, что
 число будет делиться на
число будет делиться на  .
. Запишем искомое число:
 .
. Ответ:
 .
.1. Число  ни простое и ни составное.
ни простое и ни составное.
 ни простое и ни составное.
ни простое и ни составное. 2. В результате сложения и умножения натуральных чисел всегда будем получать натуральное число.
3. В результате вычитания натуральных чисел получим натуральное число только в том случае, если уменьшаемое больше вычитаемого.
4. Деление одного натурального числа на другое не всегда выполнимо. В этом случае имеет место деление с остатком.
5. Множество делителей числа конечно, а множество чисел, кратных числу, бесконечно.
Н а п р и м е р, число имеет
имеет  делителей:
делителей:  ;
;  ;
;  ;
;  ;
;  ;
;  . Числу
. Числу  кратны числа:
кратны числа:  ,
,  ,
,  , ...
, ...
Н а п р и м е р, число
 имеет
имеет  делителей:
делителей:  ;
;  ;
;  ;
;  ;
;  ;
;  . Числу
. Числу  кратны числа:
кратны числа:  ,
,  ,
,  , ...
, ... 6. Числа, кратные числу  , записывают в виде
, записывают в виде  , где
, где  – любое натуральное число.
– любое натуральное число.
Н а п р и м е р, числа, кратные числу , можно записать так:
, можно записать так:  , где
, где  – натуральное число.
– натуральное число.
 , записывают в виде
, записывают в виде  , где
, где  – любое натуральное число.
– любое натуральное число. Н а п р и м е р, числа, кратные числу
 , можно записать так:
, можно записать так:  , где
, где  – натуральное число.
– натуральное число. 7. Рассмотрим буквенную запись чисел в десятичной позиционной системе счисления.
Н а п р и м е р, если – цифра десятков,
– цифра десятков,  – цифра единиц некоторого двузначного числа, то запишем:
– цифра единиц некоторого двузначного числа, то запишем:
 .
.
Аналогично запишем трехзначное число, у которого – цифра сотен,
– цифра сотен,  – цифра десятков,
– цифра десятков,  – цифра единиц:
– цифра единиц:
 .
.
Н а п р и м е р, если
 – цифра десятков,
– цифра десятков,  – цифра единиц некоторого двузначного числа, то запишем:
– цифра единиц некоторого двузначного числа, то запишем:  .
. Аналогично запишем трехзначное число, у которого
 – цифра сотен,
– цифра сотен,  – цифра десятков,
– цифра десятков,  – цифра единиц:
– цифра единиц:  .
.
