Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 ; (3.15)
; (3.15)  ; (3.21)
; (3.21)  ; (3.16)
; (3.16)  ; (3.22)
; (3.22)  ; (3.17)
; (3.17)  ; (3.23)
; (3.23) ; (3.18)
; (3.18)  ; (3.24)
; (3.24)  ; (3.19)
; (3.19)  ; (3.25)
; (3.25) ; (3.20)
; (3.20)  . (3.26)
. (3.26)
Логарифмом числа 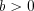 по основанию
по основанию 
 называют показатель степени
называют показатель степени  , в которую необходимо возвести
, в которую необходимо возвести  , чтобы получить
, чтобы получить  .
.
Записывают: , что равносильно
, что равносильно  .
.
Н а п р и м е р, если , то
, то  .
.
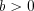 по основанию
по основанию 
 называют показатель степени
называют показатель степени  , в которую необходимо возвести
, в которую необходимо возвести  , чтобы получить
, чтобы получить  .
. Записывают:
 , что равносильно
, что равносильно  .
. Н а п р и м е р, если
 , то
, то  .
. Поскольку логарифм отрицательного числа и числа нуль не определен, то выражения  и
и  имеют смысл, а выражения
имеют смысл, а выражения  ,
,  и
и  не имеют смысла.
не имеют смысла.
 и
и  имеют смысл, а выражения
имеют смысл, а выражения  ,
,  и
и  не имеют смысла.
не имеют смысла. Свойства логарифмов:
 ; (3.15)
; (3.15)  ; (3.21)
; (3.21) ; (3.16)
; (3.16)  ; (3.22)
; (3.22)  ; (3.17)
; (3.17)  ; (3.23)
; (3.23) ; (3.18)
; (3.18)  ; (3.24)
; (3.24)  ; (3.19)
; (3.19)  ; (3.25)
; (3.25) ; (3.20)
; (3.20)  . (3.26)
. (3.26)Свойства 3.15 – 3.26 справедливы при  и
и  ,
,  и
и  ,
, 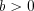 ,
,  , где числа m, n и k отличны от нуля.
, где числа m, n и k отличны от нуля.
Обратим внимание на свойство логарифма 3.21:
1) если k – нечетное число, то это равенство справедливо при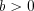 ,
,  и
и  ;
;
2) если k – четное число, то выражение определено при
определено при  ,
,  и
и  , т. е. числа а и b могут быть как положительными, так и отрицательными.
, т. е. числа а и b могут быть как положительными, так и отрицательными.
 и
и  ,
,  и
и  ,
, 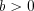 ,
,  , где числа m, n и k отличны от нуля.
, где числа m, n и k отличны от нуля. Обратим внимание на свойство логарифма 3.21:
1) если k – нечетное число, то это равенство справедливо при
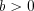 ,
,  и
и  ;
; 2) если k – четное число, то выражение
 определено при
определено при  ,
,  и
и  , т. е. числа а и b могут быть как положительными, так и отрицательными.
, т. е. числа а и b могут быть как положительными, так и отрицательными. Н а п р и м е р,  .
.
 .
.Основное логарифмическое тождество:
 . (3.27)
. (3.27)
 . (3.27)
. (3.27) Н а п р и м е р,  .
.
 .
.Общепринятые записи:
1) логарифм числа по основанию
по основанию  (десятичный логарифм) записывают:
(десятичный логарифм) записывают:
 ;
;
2) логарифм числа по основанию e (натуральный логарифм), где е – иррациональное число и
по основанию e (натуральный логарифм), где е – иррациональное число и  , записывают:
, записывают:
 .
.
1) логарифм числа
 по основанию
по основанию  (десятичный логарифм) записывают:
(десятичный логарифм) записывают:  ;
; 2) логарифм числа
 по основанию e (натуральный логарифм), где е – иррациональное число и
по основанию e (натуральный логарифм), где е – иррациональное число и  , записывают:
, записывают: .
.Пример 1. Упростите выражение ![\log_{3}^{2}\log_{3}\sqrt[3]{\sqrt[3]{3}} LaTeX formula: \log_{3}^{2}\log_{3}\sqrt[3]{\sqrt[3]{3}}](/uploads/formulas/24df34139b75626a85e535a76a3b1617f15acfa6.1.1.png) .
.
![\log_{3}^{2}\log_{3}\sqrt[3]{\sqrt[3]{3}} LaTeX formula: \log_{3}^{2}\log_{3}\sqrt[3]{\sqrt[3]{3}}](/uploads/formulas/24df34139b75626a85e535a76a3b1617f15acfa6.1.1.png) .
. Решение.
Упростим выражение![\log_{3}\sqrt[3]{\sqrt[3]{3}}=\log_{3} 3^{\frac{1}{9}} LaTeX formula: \log_{3}\sqrt[3]{\sqrt[3]{3}}=\log_{3} 3^{\frac{1}{9}}](/uploads/formulas/bb244e92f57207dd74517413c9744d1cf8f39c50.1.1.png) .
.
Упростим выражение
![\log_{3}\sqrt[3]{\sqrt[3]{3}}=\log_{3} 3^{\frac{1}{9}} LaTeX formula: \log_{3}\sqrt[3]{\sqrt[3]{3}}=\log_{3} 3^{\frac{1}{9}}](/uploads/formulas/bb244e92f57207dd74517413c9744d1cf8f39c50.1.1.png) .
. Тогда,  .
.
Ответ: .
.
 .
. Ответ:
 .
.Пример 2. Найдите значение выражения  .
.
 .
.Решение. Применяя свойства логарифмов 3.25, 3.19, 3.20 и основное логарифмическое тождество 3.27, получим:
1) ;
;
1)
 ;
;2)  .
.
 .
.Найдем значение данного выражения:
 .
.
Ответ: .
.
 .
. Ответ:
 .
. Пример 3. Вычислите  .
.
 .
.Решение. Применяя последовательно формулы 3.20, 3.21.1, 3.27 и правило раскрытия модуля числа, получим:
1) ;
;
2) .
.
Найдем значение данного выражения:
 .
.
Ответ: .
.
1)
 ;
; 2)
 .
.Найдем значение данного выражения:
 .
. Ответ:
 .
.Пример 4. Вычислите  .
.
 .
.Решение.
1. Рассмотрим разность .
.
Полагая , запишем:
, запишем:  ,
,  ,
,  .
.
Получим: .
.
1. Рассмотрим разность
 .
. Полагая
 , запишем:
, запишем:  ,
,  ,
,  .
. Получим:
 .
.3. Сложим результаты двух действий:  .
.
Ответ: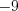 .
.
 .
. Ответ:
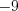 .
.Пример 5. Найдите  , если
, если  ,
,  и
и ![a=\log_{a}\sqrt[3]{121} LaTeX formula: a=\log_{a}\sqrt[3]{121}](/uploads/formulas/0fc332718d7a6214bed6747c2e3ea35e85e06022.1.1.png) .
.
 , если
, если  ,
,  и
и ![a=\log_{a}\sqrt[3]{121} LaTeX formula: a=\log_{a}\sqrt[3]{121}](/uploads/formulas/0fc332718d7a6214bed6747c2e3ea35e85e06022.1.1.png) .
.Решение.
Так как , то
, то  ,
,  ,
,  .
.
Так как , то
, то  ,
,  ,
,  .
.
Получим: , откуда
, откуда  .
.
Тогда равенство![a=\log_{a}\sqrt[3]{121} LaTeX formula: a=\log_{a}\sqrt[3]{121}](https://helpy.quali.me/uploads/formulas/0fc332718d7a6214bed6747c2e3ea35e85e06022.1.1.png) примет вид:
примет вид:
 ,
,  ,
,  ,
,  .
.
Ответ: 11.
Так как
 , то
, то  ,
,  ,
,  .
. Так как
 , то
, то  ,
,  ,
,  .
. Получим:
 , откуда
, откуда  .
. Тогда равенство
![a=\log_{a}\sqrt[3]{121} LaTeX formula: a=\log_{a}\sqrt[3]{121}](https://helpy.quali.me/uploads/formulas/0fc332718d7a6214bed6747c2e3ea35e85e06022.1.1.png) примет вид:
примет вид: ,
,  ,
,  ,
,  .
. Ответ: 11.
Пример 6. Вычислите  .
.
 .
. Учитывая, что  ,
,  , а
, а  , получим:
, получим:  .
.
 ,
,  , а
, а  , получим:
, получим:  .
.Применяя тождество  , найдем значение данного выражения:
, найдем значение данного выражения:
 .
.
Ответ: .
.
 , найдем значение данного выражения:
, найдем значение данного выражения:  .
. Ответ:
 .
.1. При возведении выражения  в степень
в степень  записывают:
записывают:
 или
или  .
.
 в степень
в степень  записывают:
записывают:  или
или  .
.2. Запись  следует понимать так:
следует понимать так:
 .
.
 следует понимать так:
следует понимать так:  .
.






 .
.
