Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 ; (1.9)
; (1.9) . (1.10)
. (1.10)  ; (1.11)
; (1.11)  ; (1.12)
; (1.12)  ; (1.13)
; (1.13)  ; (1.14)
; (1.14) . (1.15)
. (1.15)
![A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\sqrt[6]{a} LaTeX formula: A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\sqrt[6]{a}](/uploads/formulas/133119051d4eaa577a06367e04d2299925ebd770.1.1.png) ,
,  ,
,  ,
,  .
.
 .
.  ,
,  .
.
Показательным называют выражение вида  , где
, где  – действительное число.
– действительное число.
 , где
, где  – действительное число.
– действительное число. Так как при 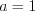 всегда будем получать тождество
всегда будем получать тождество  , а при
, а при  выражение
выражение  может быть лишено смысла, то показательные выражения целесообразно рассматривать только при условии, что
может быть лишено смысла, то показательные выражения целесообразно рассматривать только при условии, что  и
и  .
.
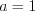 всегда будем получать тождество
всегда будем получать тождество  , а при
, а при  выражение
выражение  может быть лишено смысла, то показательные выражения целесообразно рассматривать только при условии, что
может быть лишено смысла, то показательные выражения целесообразно рассматривать только при условии, что  и
и  .
.Преобразования показательных выражений основано на свойствах степеней и свойствах арифметических корней.
Степень с целым отрицательным показателем
Для любых действительных чисел  и
и  , при условии, что
, при условии, что  и
и 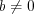 , справедливы равенства:
, справедливы равенства:
 и
и  , при условии, что
, при условии, что  и
и 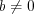 , справедливы равенства:
, справедливы равенства: ; (1.9)
; (1.9) . (1.10)
. (1.10)Свойства степеней:
 ; (1.11)
; (1.11) ; (1.12)
; (1.12)  ; (1.13)
; (1.13)  ; (1.14)
; (1.14) . (1.15)
. (1.15)Пример 1. Упростите выражение ![A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\frac{a^{0}}{\sqrt[6]{a^{-1}}} LaTeX formula: A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\frac{a^{0}}{\sqrt[6]{a^{-1}}}](/uploads/formulas/986fe911ee60f3611f3447efa2097272e5ad6f45.1.1.png) .
.
![A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\frac{a^{0}}{\sqrt[6]{a^{-1}}} LaTeX formula: A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\frac{a^{0}}{\sqrt[6]{a^{-1}}}](/uploads/formulas/986fe911ee60f3611f3447efa2097272e5ad6f45.1.1.png) .
.![A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\sqrt[6]{a} LaTeX formula: A=\frac{\sqrt[3]{a^{2}\sqrt[4]{a^{6}a^{-1}}}}{\sqrt[4]{a^{3}\sqrt[3]{a^{2}}}}-\sqrt[6]{a}](/uploads/formulas/133119051d4eaa577a06367e04d2299925ebd770.1.1.png) ,
,  ,
,  ,
,  .
.Ответ: 0.
Пример 2. Упростите выражение ![\frac{\left ( a^{\frac{1}{m}}-a^{\frac{1}{n}} \right )^{2}+2^{2}a^{\frac{m+n}{mn}}}{\left ( a^{\frac{2}{m}}-a^{\frac{2}{n}} \right )\left ( \sqrt[m]{a^{m+1}}+\sqrt[n]{a^{n+1}} \right )} LaTeX formula: \frac{\left ( a^{\frac{1}{m}}-a^{\frac{1}{n}} \right )^{2}+2^{2}a^{\frac{m+n}{mn}}}{\left ( a^{\frac{2}{m}}-a^{\frac{2}{n}} \right )\left ( \sqrt[m]{a^{m+1}}+\sqrt[n]{a^{n+1}} \right )}](/uploads/formulas/e35b8c9e45eb90c871b826a15d61424d9b212397.1.1.png) .
.
![\frac{\left ( a^{\frac{1}{m}}-a^{\frac{1}{n}} \right )^{2}+2^{2}a^{\frac{m+n}{mn}}}{\left ( a^{\frac{2}{m}}-a^{\frac{2}{n}} \right )\left ( \sqrt[m]{a^{m+1}}+\sqrt[n]{a^{n+1}} \right )} LaTeX formula: \frac{\left ( a^{\frac{1}{m}}-a^{\frac{1}{n}} \right )^{2}+2^{2}a^{\frac{m+n}{mn}}}{\left ( a^{\frac{2}{m}}-a^{\frac{2}{n}} \right )\left ( \sqrt[m]{a^{m+1}}+\sqrt[n]{a^{n+1}} \right )}](/uploads/formulas/e35b8c9e45eb90c871b826a15d61424d9b212397.1.1.png) .
.2) ![\sqrt[m]{a^{m+1}}=a^{\frac{m+1}{m}}=a^{\frac{m}{m}+\frac{1}{m}}=a^{1+\frac{1}{m}}=a\cdot a^{\frac{1}{m}} LaTeX formula: \sqrt[m]{a^{m+1}}=a^{\frac{m+1}{m}}=a^{\frac{m}{m}+\frac{1}{m}}=a^{1+\frac{1}{m}}=a\cdot a^{\frac{1}{m}}](/uploads/formulas/af7789ed99eb5d64662f7743f77a45b1074bdda4.1.1.png) ;
;
![\sqrt[m]{a^{m+1}}=a^{\frac{m+1}{m}}=a^{\frac{m}{m}+\frac{1}{m}}=a^{1+\frac{1}{m}}=a\cdot a^{\frac{1}{m}} LaTeX formula: \sqrt[m]{a^{m+1}}=a^{\frac{m+1}{m}}=a^{\frac{m}{m}+\frac{1}{m}}=a^{1+\frac{1}{m}}=a\cdot a^{\frac{1}{m}}](/uploads/formulas/af7789ed99eb5d64662f7743f77a45b1074bdda4.1.1.png) ;
; 3) ![\sqrt[n]{a^{n+1}}=a^{\frac{n+1}{n}}=a^{\frac{n}{n}+\frac{1}{n}}=a^{1+\frac{1}{n}}=a\cdot a^{\frac{1}{n}} LaTeX formula: \sqrt[n]{a^{n+1}}=a^{\frac{n+1}{n}}=a^{\frac{n}{n}+\frac{1}{n}}=a^{1+\frac{1}{n}}=a\cdot a^{\frac{1}{n}}](/uploads/formulas/a14aff913c6d5be9f241b5d70860a749146e5cdb.1.1.png) ;
;
![\sqrt[n]{a^{n+1}}=a^{\frac{n+1}{n}}=a^{\frac{n}{n}+\frac{1}{n}}=a^{1+\frac{1}{n}}=a\cdot a^{\frac{1}{n}} LaTeX formula: \sqrt[n]{a^{n+1}}=a^{\frac{n+1}{n}}=a^{\frac{n}{n}+\frac{1}{n}}=a^{1+\frac{1}{n}}=a\cdot a^{\frac{1}{n}}](/uploads/formulas/a14aff913c6d5be9f241b5d70860a749146e5cdb.1.1.png) ;
;4)  .
.
 .
.Заданное выражение примет вид:
 .
.
 .
. Полагая  и
и  , запишем:
, запишем:
 и
и  , запишем:
, запишем: .
. Применим формулы сокращенного умножения:
 ,
,  .
.Учитывая, что  и
и  , получим:
, получим:
![A=\frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})} LaTeX formula: A=\frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})}](/uploads/formulas/c1eb7eff287ff3c3a696fb0bb3dccf963f4ed1b5.1.1.png) .
.
 и
и  , получим:
, получим: ![A=\frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})} LaTeX formula: A=\frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})}](/uploads/formulas/c1eb7eff287ff3c3a696fb0bb3dccf963f4ed1b5.1.1.png) .
.Ответ: ![\frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})} LaTeX formula: \frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})}](/uploads/formulas/1e705b8e4827e50c1d578241c138950baa32cb39.1.1.png) .
.
![\frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})} LaTeX formula: \frac{1}{a(\sqrt[m]{a}-\sqrt[n]{a})}](/uploads/formulas/1e705b8e4827e50c1d578241c138950baa32cb39.1.1.png) .
.Если  , то
, то  . Выражение
. Выражение 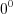 не имеет смысла.
не имеет смысла.
 , то
, то  . Выражение
. Выражение 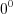 не имеет смысла.
не имеет смысла.По определению: ![\sqrt[n]{a}=a^{\frac{1}{n}} LaTeX formula: \sqrt[n]{a}=a^{\frac{1}{n}}](/uploads/formulas/89d296a3d4438201e22973da63abda647df30754.2.1.png) ,
, ![\sqrt[n]{a^{m}}=a^{\frac{m}{n}} LaTeX formula: \sqrt[n]{a^{m}}=a^{\frac{m}{n}}](/uploads/formulas/c57bd72d313d100f478da821723cfb26be593f3c.2.1.png) .
.
![\sqrt[n]{a}=a^{\frac{1}{n}} LaTeX formula: \sqrt[n]{a}=a^{\frac{1}{n}}](/uploads/formulas/89d296a3d4438201e22973da63abda647df30754.2.1.png) ,
, ![\sqrt[n]{a^{m}}=a^{\frac{m}{n}} LaTeX formula: \sqrt[n]{a^{m}}=a^{\frac{m}{n}}](/uploads/formulas/c57bd72d313d100f478da821723cfb26be593f3c.2.1.png) .
.

![\sqrt[n]{a^{m}}=a^{\frac{m}{n}} LaTeX formula: \sqrt[n]{a^{m}}=a^{\frac{m}{n}}](/uploads/formulas/c57bd72d313d100f478da821723cfb26be593f3c.1.1.png)
