Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
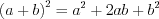 (3.1)
(3.1)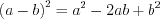 (3.2)
(3.2)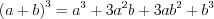 (3.3)
(3.3)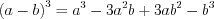 (3.4)
(3.4)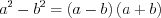 (3.5)
(3.5)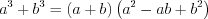 (3.6)
(3.6)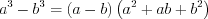 (3.7)
(3.7)
Н а п р и м е р, разложим на множители выражение , дважды применяя формулу разности квадратов 3.5:
, дважды применяя формулу разности квадратов 3.5:
 .
.
1. Вынесение за скобки общего множителя многочлена
Чтобы вынести за скобки общий множитель, необходимо каждое слагаемое алгебраической суммы разделить на этот множитель.
Н а п р и м е р, .
.
Н а п р и м е р,
 .
.Чтобы вынести общий множитель многочлена, возведенного в некоторую степень, необходимо этот множитель возвести в ту же степень, в которую возведен многочлен.
Н а п р и м е р, .
.
Н а п р и м е р,
 .
.2. Группировка членов многочлена
Группировку членов многочлена применяют, как правило, в сочетании со способом вынесения общего множителя за скобки.
Под группировкой членов многочлена понимают объединение нескольких слагаемых алгебраической суммы, то есть заключение их в скобки.
При этом слагаемые объединяют так, чтобы они имели общий множитель, а после вынесения общих множителей за скобки, слагаемые снова должны иметь общий множитель.
Н а п р и м е р,
 .
.
Под группировкой членов многочлена понимают объединение нескольких слагаемых алгебраической суммы, то есть заключение их в скобки.
При этом слагаемые объединяют так, чтобы они имели общий множитель, а после вынесения общих множителей за скобки, слагаемые снова должны иметь общий множитель.
Н а п р и м е р,

 .
.3. Применение формул сокращенного умножения
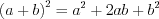 (3.1)
(3.1)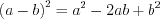 (3.2)
(3.2)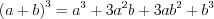 (3.3)
(3.3)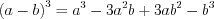 (3.4)
(3.4)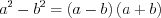 (3.5)
(3.5)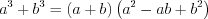 (3.6)
(3.6)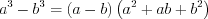 (3.7)
(3.7) Н а п р и м е р, разложим на множители выражение
 , дважды применяя формулу разности квадратов 3.5:
, дважды применяя формулу разности квадратов 3.5:  .
.4. Выделение полного квадрата
Пример 2. Разложите на множители многочлен  .
.
Решение.
Применим метод группировки:
 ,
,
 ,
,
 ,
,
 .
.
Применим формулу разности квадратов 3.5:
 .
.
Ответ: .
.
 .
.Решение.
Применим метод группировки:
 ,
,  ,
,  ,
,  .
.Применим формулу разности квадратов 3.5:
 .
.Ответ:
 .
.Пример 3. Разложите на множители выражение  .
.
Решение.
Применим формулу квадрата разности 3.2:
 ,
,  .
.
Применим формулу разности квадратов 3.5:
 .
.
Ответ: .
.
 .
.Решение.
Применим формулу квадрата разности 3.2:
 ,
,  .
. Применим формулу разности квадратов 3.5:
 .
.Ответ:
 .
.Пример 4. Разложите на множители выражение  .
.
Решение. Запишем трехчлен в виде:
 .
.
Дополним его до квадрата разности 3.2:
 ,
,
 .
.
Применим формулу разности квадратов 3.5:
 ,
,
 .
.
Ответ: .
.
 .
.Решение. Запишем трехчлен в виде:
 .
.Дополним его до квадрата разности 3.2:
 ,
, .
.Применим формулу разности квадратов 3.5:
 ,
,  .
.Ответ:
 .
.1. Для всех  справедливы равенства:
справедливы равенства:
1) ;
;
2) .
.
Н а п р и м е р: 1) ; 2)
; 2)  .
.
 справедливы равенства:
справедливы равенства:1)
 ;
; 2)
 .
. Н а п р и м е р: 1)
 ; 2)
; 2)  .
.2. Существуют и другие способы разложения многочленов на множители:
1) квадратный трехчлен можно разложить на линейные множители по формуле:
можно разложить на линейные множители по формуле:
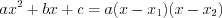 ,
,
где и
и  – корни этого трехчлена;
– корни этого трехчлена;
1) квадратный трехчлен
 можно разложить на линейные множители по формуле:
можно разложить на линейные множители по формуле: 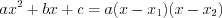 ,
, где
 и
и  – корни этого трехчлена;
– корни этого трехчлена;2) многочлен  можно разложить на множители по формуле:
можно разложить на множители по формуле:
 ,
,
где ,
,  , … ,
, … ,  все корни этого многочлена;
все корни этого многочлена;
 можно разложить на множители по формуле:
можно разложить на множители по формуле:  ,
, где
 ,
,  , … ,
, … ,  все корни этого многочлена;
все корни этого многочлена; 3) если  – корень кратности
– корень кратности  многочлена
многочлена 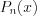 , то разложение этого многочлена на множители примет вид:
, то разложение этого многочлена на множители примет вид:
 .
.
 – корень кратности
– корень кратности  многочлена
многочлена 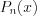 , то разложение этого многочлена на множители примет вид:
, то разложение этого многочлена на множители примет вид: .
.


 ,
,  ,
,  ,
,  .
.  .
. .
. 
 .
.