Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты



Одночлены
Одночленом называют алгебраическое выражение, представленное в виде произведения чисел и переменных величин.
Н а п р и м е р, ,
,  и
и  – одночлены.
– одночлены.
Действительное число, например, число 5 также одночлен, так как его можно записать в виде или, например, в виде
или, например, в виде  .
.
Н а п р и м е р,
 ,
,  и
и  – одночлены.
– одночлены. Действительное число, например, число 5 также одночлен, так как его можно записать в виде
 или, например, в виде
или, например, в виде  .
.Одночлен имеет стандартный вид, если он имеет только один числовой множитель, а каждая из переменных встречается в его записи только один раз. Числовой множитель называют коэффициентом одночлена.
Если коэффициент одночлена равен 0, то его называют нулевым одночленом.
Н а п р и м е р, – нулевой одночлен.
– нулевой одночлен.
Н а п р и м е р,
 – нулевой одночлен.
– нулевой одночлен.Одночлены, которые имеют одинаковую переменную часть, называются подобными.
Чтобы сложить подобные одночлены, необходимо сложить их коэффициенты, а переменную часть переписать.
Н а п р и м е р, одночлены и
и  подобные, а их сумма равна
подобные, а их сумма равна  .
.
Чтобы сложить подобные одночлены, необходимо сложить их коэффициенты, а переменную часть переписать.
Н а п р и м е р, одночлены
 и
и  подобные, а их сумма равна
подобные, а их сумма равна  .
. Степенью одночлена называют сумму показателей степеней всех входящих в него переменных.
Н а п р и м е р: степень одночлена равна 1; степень одночлена
равна 1; степень одночлена  равна 5.
равна 5.
Н а п р и м е р: степень одночлена
 равна 1; степень одночлена
равна 1; степень одночлена  равна 5.
равна 5.Если одночлен представлен отличным от нуля числом, то его степень равна 0.
Н а п р и м е р, числа –260 и 0,5 – одночлены, степень которых равна 0.
Н а п р и м е р, числа –260 и 0,5 – одночлены, степень которых равна 0.
Нулевым одночленам не приписывают никакую степень.
Многочлены
Многочленом называют алгебраическое выражение, представленное в виде суммы нескольких одночленов.
Н а п р и м е р, и
и  – многочлены.
– многочлены.
Н а п р и м е р,
 и
и  – многочлены.
– многочлены. Многочлен имеет стандартный вид, если все одночлены имеют стандартный вид, и среди них нет подобных.
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в него одночленов.
Н а п р и м е р, степень многочлена равна 4.
равна 4.
Н а п р и м е р, степень многочлена
 равна 4.
равна 4.Чтобы умножить одночлен на многочлен, необходимо умножить одночлен на каждый член многочлена и полученные произведения сложить.
Н а п р и м е р, .
.
Н а п р и м е р,
 .
.При умножении многочлена на число 1, многочлен не изменится, а при умножении многочлена на число –1, получим многочлен, каждый член которого будет иметь противоположный коэффициент.
Н а п р и м е р, ;
; .
.
Н а п р и м е р,
 ;
; .
.Правило раскрытия скобок:
1. Если перед скобкой стоит знак «+» (этот знак не ставят), то скобки опускают, а выражение, стоящее в скобках, переписывают без изменений.2.
Если перед скобкой стоит знак «–», то скобки опускают, а выражение, стоящее в скобках, умножают на число –1.
Н а п р и м е р, .
.
1. Если перед скобкой стоит знак «+» (этот знак не ставят), то скобки опускают, а выражение, стоящее в скобках, переписывают без изменений.2.
Если перед скобкой стоит знак «–», то скобки опускают, а выражение, стоящее в скобках, умножают на число –1.
Н а п р и м е р,
 .
.Чтобы умножить многочлен на многочлен, необходимо каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Н а п р и м е р: .
.
Н а п р и м е р:
 .
.Многочленом степени  от одной переменной
от одной переменной  называют выражение вида
называют выражение вида  при
при 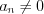 и
и  .
.
Числа называют коэффициентами многочлена, при этом число
называют коэффициентами многочлена, при этом число 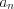 называют старшим коэффициентом многочлена, а число
называют старшим коэффициентом многочлена, а число 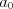 – свободным членом. Коэффициенты многочлена за исключением его старшего коэффициента, могут быть равны нулю.
– свободным членом. Коэффициенты многочлена за исключением его старшего коэффициента, могут быть равны нулю.
Н а п р и м е р: – многочлен первой степени, а
– многочлен первой степени, а  – многочлен третьей степени.
– многочлен третьей степени.
 от одной переменной
от одной переменной  называют выражение вида
называют выражение вида  при
при 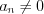 и
и  .
. Числа
 называют коэффициентами многочлена, при этом число
называют коэффициентами многочлена, при этом число 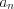 называют старшим коэффициентом многочлена, а число
называют старшим коэффициентом многочлена, а число 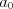 – свободным членом. Коэффициенты многочлена за исключением его старшего коэффициента, могут быть равны нулю.
– свободным членом. Коэффициенты многочлена за исключением его старшего коэффициента, могут быть равны нулю.Н а п р и м е р:
 – многочлен первой степени, а
– многочлен первой степени, а  – многочлен третьей степени.
– многочлен третьей степени.Многочлен вида  называют многочленом нулевой степени, а если
называют многочленом нулевой степени, а если  , то имеем нулевой многочлен.
, то имеем нулевой многочлен.
Н а п р и м е р, – многочлен нулевой степени, а
– многочлен нулевой степени, а  – нулевой многочлен.
– нулевой многочлен.
 называют многочленом нулевой степени, а если
называют многочленом нулевой степени, а если  , то имеем нулевой многочлен.
, то имеем нулевой многочлен.Н а п р и м е р,
 – многочлен нулевой степени, а
– многочлен нулевой степени, а  – нулевой многочлен.
– нулевой многочлен. Корнем многочлена  называют такое число
называют такое число  , что
, что  .
.
Н а п р и м е р, число является корнем многочлена
является корнем многочлена  , так как
, так как  .
.
 называют такое число
называют такое число  , что
, что  .
.Н а п р и м е р, число
 является корнем многочлена
является корнем многочлена  , так как
, так как  .
. Число  называют корнем кратности
называют корнем кратности  многочлена
многочлена  , если справедливо равенство
, если справедливо равенство  , где
, где  – многочлен степени
– многочлен степени  ,
,  и
и  – натуральные числа
– натуральные числа  и
и  .
.
 называют корнем кратности
называют корнем кратности  многочлена
многочлена  , если справедливо равенство
, если справедливо равенство  , где
, где  – многочлен степени
– многочлен степени  ,
,  и
и  – натуральные числа
– натуральные числа  и
и  .
.Деление многочленов
Деление многочленов выполняют аналогично делению целых чисел.
Делят старший член многочлена-делимого на старший член многочлена-делителя, затем частное умножают на многочлен-делитель и полученное произведение вычитают из многочлена-делимого.
Многочлен-первый остаток аналогичным образом делят на многочлен-делитель.
Деление продолжают до тех пор пока не получат остаток нуль или степень многочлена-остатка не будет меньше степени многочлена-делителя.
Н а п р и м е р,
Делят старший член многочлена-делимого на старший член многочлена-делителя, затем частное умножают на многочлен-делитель и полученное произведение вычитают из многочлена-делимого.
Многочлен-первый остаток аналогичным образом делят на многочлен-делитель.
Деление продолжают до тех пор пока не получат остаток нуль или степень многочлена-остатка не будет меньше степени многочлена-делителя.
Н а п р и м е р,

Результат деления записывают так:
 .
.
 .
.Теорема Безу. Остаток от деления многочлена
от деления многочлена 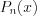 на двучлен
на двучлен  равен значению многочлена при
равен значению многочлена при  , то есть
, то есть  .
.
 от деления многочлена
от деления многочлена 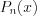 на двучлен
на двучлен  равен значению многочлена при
равен значению многочлена при  , то есть
, то есть  .
.Следствие 1. Для делимости многочлена 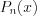 на двучлен
на двучлен  необходимо и достаточно, чтобы число
необходимо и достаточно, чтобы число  было корнем многочлена
было корнем многочлена 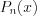 .
.
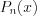 на двучлен
на двучлен  необходимо и достаточно, чтобы число
необходимо и достаточно, чтобы число  было корнем многочлена
было корнем многочлена 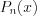 .
.Следствие 2. Если  – все корни многочлена
– все корни многочлена 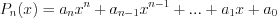 , то этот многочлен можно разложить на множители следующим образом:
, то этот многочлен можно разложить на множители следующим образом:  .
.
 – все корни многочлена
– все корни многочлена 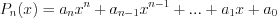 , то этот многочлен можно разложить на множители следующим образом:
, то этот многочлен можно разложить на множители следующим образом:  .
. Если  – корень кратности
– корень кратности  многочлена
многочлена 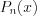 , то разложение этого многочлена на множители примет вид:
, то разложение этого многочлена на множители примет вид:  .
.
 – корень кратности
– корень кратности  многочлена
многочлена 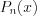 , то разложение этого многочлена на множители примет вид:
, то разложение этого многочлена на множители примет вид:  .
.Теорема о целых корнях. Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
Следствие. При отыскании целых корней многочлена с целыми коэффициентами достаточно рассмотреть делители свободного члена.
Пример 1. Найдите коэффициент и степень одночлена  .
.
Решение. Приведем одночлен к стандартному виду:
 .
.
Коэффициент одночлена равен числу .
.
Найдем степень одночлена, складывая показатели степеней переменных:
 .
.
Ответ: ;
;  .
.
 .
. Решение. Приведем одночлен к стандартному виду:
 .
.Коэффициент одночлена равен числу
 .
.Найдем степень одночлена, складывая показатели степеней переменных:
 .
. Ответ:
 ;
;  .
.Пример 2. Найдите степень многочлена  .
.
Решение. Приведем многочлен к стандартному виду:
 .
.
Найдем степени одночленов, входящих в состав многочлена:
1) степень одночлена равна
равна  ;
;
2) степень одночлена равна
равна  ;
;
3) степень одночлена равна
равна  .
.
Следовательно, степень многочлена равна .
.
Ответ: .
.
 .
.Решение. Приведем многочлен к стандартному виду:
 .
. Найдем степени одночленов, входящих в состав многочлена:
1) степень одночлена
 равна
равна  ;
;2) степень одночлена
 равна
равна  ;
;3) степень одночлена
 равна
равна  .
.Следовательно, степень многочлена равна
 .
.Ответ:
 .
.Пример 3. Найдите корни многочлена  .
.
Решение. Найдем целые корни многочлена.
Согласно теореме о целых корнях, ими могут быть только делители свободного члена, то есть числа –1 и 1.
Выполним проверку:
 ,
,
 .
.
Так как
 , то число –1 не является корнем многочлена.
, то число –1 не является корнем многочлена.
А так как , то число 1 – целый корень многочлена.
, то число 1 – целый корень многочлена.
Тогда, согласно следствию из теоремы Безу, многочлен делится на двучлен
делится на двучлен  .
.
Выполним деление многочленов:
 .
.Решение. Найдем целые корни многочлена.
Согласно теореме о целых корнях, ими могут быть только делители свободного члена, то есть числа –1 и 1.
Выполним проверку:
 ,
, .
. Так как

 , то число –1 не является корнем многочлена.
, то число –1 не является корнем многочлена.А так как
 , то число 1 – целый корень многочлена.
, то число 1 – целый корень многочлена. Тогда, согласно следствию из теоремы Безу, многочлен
 делится на двучлен
делится на двучлен  .
.Выполним деление многочленов:

Запишем результат деления:  .
.
Найдем корни квадратного трехчлена .
.
Получим: ,
,  ,
,  .
.
Следовательно, многочлен имеет три корня:
имеет три корня:  .
.
Ответ: .
.
 .
.Найдем корни квадратного трехчлена
 .
. Получим:
 ,
,  ,
,  .
. Следовательно, многочлен
 имеет три корня:
имеет три корня:  .
. Ответ:
 .
.Пример 4. Найдите остаток  от деления многочлена
от деления многочлена  на двучлен
на двучлен  .
.
Решение. Вычислим значение многочлена при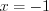 :
:

 .
.
Ответ: .
.
 от деления многочлена
от деления многочлена  на двучлен
на двучлен  .
. Решение. Вычислим значение многочлена при
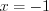 :
: 
 .
. Ответ:
 .
.Пример 5. Найдите все целые значения  , при которых дробь
, при которых дробь  является целым числом.
является целым числом.
 , при которых дробь
, при которых дробь  является целым числом.
является целым числом.Решение. Упростим дробь:
 .
.
Разделим числитель дроби на ее знаменатель:
 .
.Разделим числитель дроби на ее знаменатель:

Запишем результат деления:  .
.
 .
.Очевидно, что дробь  будет целым числом, если 49 разделится без остатка на
будет целым числом, если 49 разделится без остатка на  , то есть если число
, то есть если число  будет делителем числа 49.
будет делителем числа 49.
Запишем делители числа 49: .
.
Решим уравнения:
1) ,
, ;
;
2) ;
;
3) ;
;
4) ;
;
5) ;
;
6) .
.
Так как, согласно условию задачи, – целое число, то
– целое число, то  ,
,  и
и  .
.
Ответ: .
.
 будет целым числом, если 49 разделится без остатка на
будет целым числом, если 49 разделится без остатка на  , то есть если число
, то есть если число  будет делителем числа 49.
будет делителем числа 49. Запишем делители числа 49:
 .
. Решим уравнения:
1)
 ,
, ;
; 2)
 ;
;3)
 ;
;4)
 ;
;5)
 ;
;6)
 .
. Так как, согласно условию задачи,
 – целое число, то
– целое число, то  ,
,  и
и  .
.Ответ:
 .
.1. Если коэффициент одночлена равен 1 или –1, то цифру 1, как правило, не записывают, а пишут только его переменную часть.
Н а п р и м е р: ;
; .
.
Н а п р и м е р:
 ;
; .
.2. Одночлены также являются многочленами.

