Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 ; (1.9)
; (1.9)  . (1.10)
. (1.10)  ; (1.11)
; (1.11)  ; (1.12)
; (1.12)  ; (1.13)
; (1.13)  ; (1.14)
; (1.14) . (1.15)
. (1.15)![\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab} LaTeX formula: \sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}](/uploads/formulas/d216f198ab3c0ec1d37683f9d27ac005c12d50b8.1.1.png) ; (1.16)
; (1.16) ![\sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}=a^{\frac{1}{mn}} LaTeX formula: \sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}=a^{\frac{1}{mn}}](/uploads/formulas/ffcc64a8cbd5f2762c9582ee70b9ac3130093250.1.1.png) ; (1.17)
; (1.17)![\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}=\left ( \frac{a}{b} \right )^{\frac{1}{n}} LaTeX formula: \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}=\left ( \frac{a}{b} \right )^{\frac{1}{n}}](/uploads/formulas/6b12d2e89b4bf8086f5c0f98d1e5226cf025bbb2.1.1.png) ; (1.18)
; (1.18) ![\sqrt[2n]{a^{2n}}=\left | a \right | LaTeX formula: \sqrt[2n]{a^{2n}}=\left | a \right |](/uploads/formulas/cbd9b90891fcdca819ec0b57a22ff56c301c4728.1.1.png) ; (1.19)
; (1.19)![\sqrt[2n+1]{a^{2n+1}}=a LaTeX formula: \sqrt[2n+1]{a^{2n+1}}=a](/uploads/formulas/48d600dfe62d7c443aa76c00d36eb0047445ab1d.1.1.png) ; (1.20)
; (1.20) ![\sqrt[n]{a}=\sqrt[kn]{a^{k}} LaTeX formula: \sqrt[n]{a}=\sqrt[kn]{a^{k}}](/uploads/formulas/157374f55534f386aad28fa4a34ffef4e4fde3ac.2.1.png) . (1.21)
. (1.21)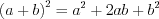 ; (3.1)
; (3.1)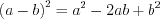 ; (3.2)
; (3.2)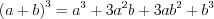 ; (3.3)
; (3.3)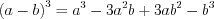 ; (3.4)
; (3.4)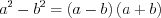 ; (3.5)
; (3.5)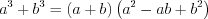 ; (3.6)
; (3.6)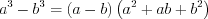 . (3.7)
. (3.7) (3.1.1)
(3.1.1)
![A=\sqrt[4]{216x^{3}\left ( 5+2\sqrt{6} \right )}\sqrt[4]{6x\left ( 5-2\sqrt{6} \right )} LaTeX formula: A=\sqrt[4]{216x^{3}\left ( 5+2\sqrt{6} \right )}\sqrt[4]{6x\left ( 5-2\sqrt{6} \right )}](/uploads/formulas/4c7364f60e4f564f43452ed2ac95d25dde8ce85b.1.1.png) ,
, ![A=\sqrt[4]{(6x)^{4}(5+2\sqrt{6})(5-2\sqrt{6})} LaTeX formula: A=\sqrt[4]{(6x)^{4}(5+2\sqrt{6})(5-2\sqrt{6})}](/uploads/formulas/0a2eee9a93b05542d0231e819b8b8320e7a827c2.1.1.png) ,
, ![A=\sqrt[4]{(6x)^{4}(25-24)}=\sqrt[4]{(6x)^{4}}=6x LaTeX formula: A=\sqrt[4]{(6x)^{4}(25-24)}=\sqrt[4]{(6x)^{4}}=6x](/uploads/formulas/6a7a5c0cd9df0973ae6d9818547a104015c6d744.1.1.png) .
.
 ,
,  ,
,  ,
,  .
. ![\sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}}= LaTeX formula: \sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}}=](/uploads/formulas/260115c50055a7ec412b29b29b5215daa618ef0f.1.1.png)
![\sqrt[3]{\frac{(10-7\sqrt{2})^{2}}{(10+7\sqrt{2})(10-7\sqrt{2})}} LaTeX formula: \sqrt[3]{\frac{(10-7\sqrt{2})^{2}}{(10+7\sqrt{2})(10-7\sqrt{2})}}](/uploads/formulas/7de3d021e8326d82829ba4ad9540c683bb2d4f6d.1.1.png)
![=\sqrt[3]{\frac{100-140\sqrt{2}+98}{100-98}} LaTeX formula: =\sqrt[3]{\frac{100-140\sqrt{2}+98}{100-98}}](/uploads/formulas/627cbb372cb3c3a5ffed4ca69715cf30ea6b6413.1.1.png)
![=\sqrt[3]{\frac{2(99-70\sqrt{2})}{2}}= LaTeX formula: \sqrt[3]{\frac{2(99-70\sqrt{2})}{2}}=](/uploads/formulas/eaa42e1532a7df2e2a91f5fe3e75e413a20629e7.1.1.png)
![\sqrt[3]{99-70\sqrt{2}} LaTeX formula: \sqrt[3]{99-70\sqrt{2}}](/uploads/formulas/fb82f210a6ed693f875f278dfeaf98991447c16f.1.1.png) .
. .
.![3-2\sqrt{2}=\sqrt[3]{(3-2\sqrt{2})^{3}}= LaTeX formula: 3-2\sqrt{2}=\sqrt[3]{(3-2\sqrt{2})^{3}}=](/uploads/formulas/76cec947cbb29d2f8c0803a77b13db64e093998c.1.1.png)
![\sqrt[3]{27-54\sqrt{2}+72-16\sqrt{2}}=\sqrt[3]{99-70\sqrt{2}} LaTeX formula: \sqrt[3]{27-54\sqrt{2}+72-16\sqrt{2}}=\sqrt[3]{99-70\sqrt{2}}](/uploads/formulas/7c51e2e38e629ac1fad483ad59775b847f99f373.1.1.png) .
. .
.
 .
.
 .
.
Иррациональными называют выражения, содержащие переменную под знаком радикала (корня).
Н а п р и м е р, выражения  и
и ![\frac{\sqrt[3]{3y-2}}{x-2} LaTeX formula: \frac{\sqrt[3]{3y-2}}{x-2}](/uploads/formulas/276eb9fb0e3be736e64750aa21d8740b371e23f7.1.1.png) – иррациональные.
– иррациональные.
 и
и ![\frac{\sqrt[3]{3y-2}}{x-2} LaTeX formula: \frac{\sqrt[3]{3y-2}}{x-2}](/uploads/formulas/276eb9fb0e3be736e64750aa21d8740b371e23f7.1.1.png) – иррациональные.
– иррациональные. Выполняя тождественные преобразования иррациональных выражений необходимо учитывать, что:
1) выражения, записанные под знаками корней четной степени, не могут быть отрицательными;
2) область определения иррационального выражения может измениться и в результате сокращения дроби на множитель, содержащий переменную, и в результате возведения обеих частей равенства в четную степень.
В процессе преобразований иррациональных выражений используют формулы сокращенного умножения, действия с алгебраическими дробями, способы разложения многочленов на множители.
Степень с целым отрицательным показателем
Для любых действительных чисел  и
и  , при условии, что
, при условии, что  и
и 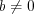 , справедливы равенства:
, справедливы равенства:
 и
и  , при условии, что
, при условии, что  и
и 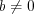 , справедливы равенства:
, справедливы равенства: ; (1.9)
; (1.9)  . (1.10)
. (1.10)Свойства степеней:
 ; (1.11)
; (1.11)  ; (1.12)
; (1.12)  ; (1.13)
; (1.13)  ; (1.14)
; (1.14) . (1.15)
. (1.15)Свойства корней:
![\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab} LaTeX formula: \sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}](/uploads/formulas/d216f198ab3c0ec1d37683f9d27ac005c12d50b8.1.1.png) ; (1.16)
; (1.16) ![\sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}=a^{\frac{1}{mn}} LaTeX formula: \sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}=a^{\frac{1}{mn}}](/uploads/formulas/ffcc64a8cbd5f2762c9582ee70b9ac3130093250.1.1.png) ; (1.17)
; (1.17)![\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}=\left ( \frac{a}{b} \right )^{\frac{1}{n}} LaTeX formula: \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}=\left ( \frac{a}{b} \right )^{\frac{1}{n}}](/uploads/formulas/6b12d2e89b4bf8086f5c0f98d1e5226cf025bbb2.1.1.png) ; (1.18)
; (1.18) ![\sqrt[2n]{a^{2n}}=\left | a \right | LaTeX formula: \sqrt[2n]{a^{2n}}=\left | a \right |](/uploads/formulas/cbd9b90891fcdca819ec0b57a22ff56c301c4728.1.1.png) ; (1.19)
; (1.19)![\sqrt[2n+1]{a^{2n+1}}=a LaTeX formula: \sqrt[2n+1]{a^{2n+1}}=a](/uploads/formulas/48d600dfe62d7c443aa76c00d36eb0047445ab1d.1.1.png) ; (1.20)
; (1.20) ![\sqrt[n]{a}=\sqrt[kn]{a^{k}} LaTeX formula: \sqrt[n]{a}=\sqrt[kn]{a^{k}}](/uploads/formulas/157374f55534f386aad28fa4a34ffef4e4fde3ac.2.1.png) . (1.21)
. (1.21)Формулы сокращенного умножения:
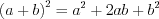 ; (3.1)
; (3.1)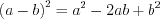 ; (3.2)
; (3.2)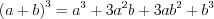 ; (3.3)
; (3.3)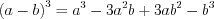 ; (3.4)
; (3.4)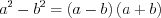 ; (3.5)
; (3.5)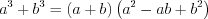 ; (3.6)
; (3.6)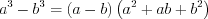 . (3.7)
. (3.7) (3.1.1)
(3.1.1)Пример 1. Упростите выражение ![\sqrt[4]{216x^{3}(5+2\sqrt{6})}\cdot \sqrt{3\sqrt{2x}-2\sqrt{3x}} LaTeX formula: \sqrt[4]{216x^{3}(5+2\sqrt{6})}\cdot \sqrt{3\sqrt{2x}-2\sqrt{3x}}](/uploads/formulas/25a02c69bf97cfa552748dea5013626a94f53d42.1.1.png) .
.
![\sqrt[4]{216x^{3}(5+2\sqrt{6})}\cdot \sqrt{3\sqrt{2x}-2\sqrt{3x}} LaTeX formula: \sqrt[4]{216x^{3}(5+2\sqrt{6})}\cdot \sqrt{3\sqrt{2x}-2\sqrt{3x}}](/uploads/formulas/25a02c69bf97cfa552748dea5013626a94f53d42.1.1.png) .
.Решение. Выполним последовательно следующие действия.
![A=\sqrt[4]{216x^{3}\left ( 5+2\sqrt{6} \right )}\sqrt[4]{6x\left ( 5-2\sqrt{6} \right )} LaTeX formula: A=\sqrt[4]{216x^{3}\left ( 5+2\sqrt{6} \right )}\sqrt[4]{6x\left ( 5-2\sqrt{6} \right )}](/uploads/formulas/4c7364f60e4f564f43452ed2ac95d25dde8ce85b.1.1.png) ,
, ![A=\sqrt[4]{(6x)^{4}(5+2\sqrt{6})(5-2\sqrt{6})} LaTeX formula: A=\sqrt[4]{(6x)^{4}(5+2\sqrt{6})(5-2\sqrt{6})}](/uploads/formulas/0a2eee9a93b05542d0231e819b8b8320e7a827c2.1.1.png) ,
, ![A=\sqrt[4]{(6x)^{4}(25-24)}=\sqrt[4]{(6x)^{4}}=6x LaTeX formula: A=\sqrt[4]{(6x)^{4}(25-24)}=\sqrt[4]{(6x)^{4}}=6x](/uploads/formulas/6a7a5c0cd9df0973ae6d9818547a104015c6d744.1.1.png) .
. Ответ:  .
.
 .
.Пример 2. Упростите выражение ![A=\frac{\sqrt[3]{9x^{5}}-4x}{\sqrt[3]{3x^{2}}-2\sqrt[3]{x}}-2x^{\frac{2}{3}} LaTeX formula: A=\frac{\sqrt[3]{9x^{5}}-4x}{\sqrt[3]{3x^{2}}-2\sqrt[3]{x}}-2x^{\frac{2}{3}}](/uploads/formulas/b7f47fc717426dc4db1607a1da83868f5cdd80f9.1.1.png) .
.
![A=\frac{\sqrt[3]{9x^{5}}-4x}{\sqrt[3]{3x^{2}}-2\sqrt[3]{x}}-2x^{\frac{2}{3}} LaTeX formula: A=\frac{\sqrt[3]{9x^{5}}-4x}{\sqrt[3]{3x^{2}}-2\sqrt[3]{x}}-2x^{\frac{2}{3}}](/uploads/formulas/b7f47fc717426dc4db1607a1da83868f5cdd80f9.1.1.png) .
. ,
,  ,
,  ,
,  .
. Учитывая подстановку ![\sqrt[3]{x}=y LaTeX formula: \sqrt[3]{x}=y](/uploads/formulas/a85cdcd4bc377d6dcfca6ea15c4bf7c06fca52b0.1.1.png) и
и ![\sqrt[3]{3}=a LaTeX formula: \sqrt[3]{3}=a](/uploads/formulas/f4d611030baef3a048a46effc032cb715437374d.1.1.png) , запишем результат преобразования:
, запишем результат преобразования:
![A=\sqrt[3]{3}x LaTeX formula: A=\sqrt[3]{3}x](/uploads/formulas/9ca03c1ef9db4a9cbb31be8bfda8be574585b294.1.1.png) .
.
![\sqrt[3]{x}=y LaTeX formula: \sqrt[3]{x}=y](/uploads/formulas/a85cdcd4bc377d6dcfca6ea15c4bf7c06fca52b0.1.1.png) и
и ![\sqrt[3]{3}=a LaTeX formula: \sqrt[3]{3}=a](/uploads/formulas/f4d611030baef3a048a46effc032cb715437374d.1.1.png) , запишем результат преобразования:
, запишем результат преобразования: ![A=\sqrt[3]{3}x LaTeX formula: A=\sqrt[3]{3}x](/uploads/formulas/9ca03c1ef9db4a9cbb31be8bfda8be574585b294.1.1.png) .
.Ответ: ![\sqrt[3]{3}x LaTeX formula: \sqrt[3]{3}x](/uploads/formulas/7901a08c274e6e78d35f48f7258c99e26ce91338.1.1.png) .
.
![\sqrt[3]{3}x LaTeX formula: \sqrt[3]{3}x](/uploads/formulas/7901a08c274e6e78d35f48f7258c99e26ce91338.1.1.png) .
.Пример 3. Найдите  , если
, если  .
.
 , если
, если  .
.Решение. Положим  .
.
Найдем произведения правых и левых частей равенств:
 и
и  .
.
 .
. Найдем произведения правых и левых частей равенств:
 и
и  .
. Получим:  .
.
 .
. Пример 4. Проверьте справедливость равенства ![-\frac{1-\sqrt{2}}{\sqrt{2}+1}=\sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}} LaTeX formula: -\frac{1-\sqrt{2}}{\sqrt{2}+1}=\sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}}](/uploads/formulas/a4999047f61c583e20a79e66a1e1312c54e81120.1.1.png) .
.
![-\frac{1-\sqrt{2}}{\sqrt{2}+1}=\sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}} LaTeX formula: -\frac{1-\sqrt{2}}{\sqrt{2}+1}=\sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}}](/uploads/formulas/a4999047f61c583e20a79e66a1e1312c54e81120.1.1.png) .
.Решение. Выполним преобразования правой части равенства, умножая числитель и знаменатель дроби на выражение сопряженное выражению, записанному в знаменателе дроби, и применяя формулы 3.2 и 3.5:
![\sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}}= LaTeX formula: \sqrt[3]{\frac{10-7\sqrt{2}}{10+7\sqrt{2}}}=](/uploads/formulas/260115c50055a7ec412b29b29b5215daa618ef0f.1.1.png)
![\sqrt[3]{\frac{(10-7\sqrt{2})^{2}}{(10+7\sqrt{2})(10-7\sqrt{2})}} LaTeX formula: \sqrt[3]{\frac{(10-7\sqrt{2})^{2}}{(10+7\sqrt{2})(10-7\sqrt{2})}}](/uploads/formulas/7de3d021e8326d82829ba4ad9540c683bb2d4f6d.1.1.png)
![=\sqrt[3]{\frac{100-140\sqrt{2}+98}{100-98}} LaTeX formula: =\sqrt[3]{\frac{100-140\sqrt{2}+98}{100-98}}](/uploads/formulas/627cbb372cb3c3a5ffed4ca69715cf30ea6b6413.1.1.png)
![=\sqrt[3]{\frac{2(99-70\sqrt{2})}{2}}= LaTeX formula: \sqrt[3]{\frac{2(99-70\sqrt{2})}{2}}=](/uploads/formulas/eaa42e1532a7df2e2a91f5fe3e75e413a20629e7.1.1.png)
![\sqrt[3]{99-70\sqrt{2}} LaTeX formula: \sqrt[3]{99-70\sqrt{2}}](/uploads/formulas/fb82f210a6ed693f875f278dfeaf98991447c16f.1.1.png) .
.Аналогичным образом выполним преобразования левой части равенства:
 .
.Поскольку правая часть равенства представлена корнем третьей степени, то, применяя формулы 1.21 и 3.4, запишем:
![3-2\sqrt{2}=\sqrt[3]{(3-2\sqrt{2})^{3}}= LaTeX formula: 3-2\sqrt{2}=\sqrt[3]{(3-2\sqrt{2})^{3}}=](/uploads/formulas/76cec947cbb29d2f8c0803a77b13db64e093998c.1.1.png)
![\sqrt[3]{27-54\sqrt{2}+72-16\sqrt{2}}=\sqrt[3]{99-70\sqrt{2}} LaTeX formula: \sqrt[3]{27-54\sqrt{2}+72-16\sqrt{2}}=\sqrt[3]{99-70\sqrt{2}}](/uploads/formulas/7c51e2e38e629ac1fad483ad59775b847f99f373.1.1.png) .
.Ответ: Равенство справедливо.
Пример 5. Найдите значение выражения ![A=(\sqrt[3]{135}+\sqrt[3]{40}):\sqrt[8]{(5\cdot \sqrt[3]{5})^{2}} LaTeX formula: A=(\sqrt[3]{135}+\sqrt[3]{40}):\sqrt[8]{(5\cdot \sqrt[3]{5})^{2}}](/uploads/formulas/bcf1407efb6a099850b2721edc9e7e9aea61914a.1.1.png) .
.
![A=(\sqrt[3]{135}+\sqrt[3]{40}):\sqrt[8]{(5\cdot \sqrt[3]{5})^{2}} LaTeX formula: A=(\sqrt[3]{135}+\sqrt[3]{40}):\sqrt[8]{(5\cdot \sqrt[3]{5})^{2}}](/uploads/formulas/bcf1407efb6a099850b2721edc9e7e9aea61914a.1.1.png) .
. .
. Ответ: 5.
Пример 6. Найдите значение выражения ![\left ( \sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}}-\sqrt[5]{(1-\sqrt{2})^{5}} \right )^{-4} LaTeX formula: \left ( \sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}}-\sqrt[5]{(1-\sqrt{2})^{5}} \right )^{-4}](/uploads/formulas/4b879cd579ed75769ab55550b8c4c133ac97897c.1.1.png) .
.
![\left ( \sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}}-\sqrt[5]{(1-\sqrt{2})^{5}} \right )^{-4} LaTeX formula: \left ( \sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}}-\sqrt[5]{(1-\sqrt{2})^{5}} \right )^{-4}](/uploads/formulas/4b879cd579ed75769ab55550b8c4c133ac97897c.1.1.png) .
.Упростим выражение ![\sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}} LaTeX formula: \sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}}](/uploads/formulas/1ed8c74a421f3df3864687b17698d8dc5cbfb04d.1.1.png) .
.
Поскольку ,
,
то, учитывая, что , запишем:
, запишем:
![\sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}} LaTeX formula: \sqrt[4]{\left ( \sqrt{2}-\frac{3}{2}\right )^{4}}](/uploads/formulas/1ed8c74a421f3df3864687b17698d8dc5cbfb04d.1.1.png) .
. Поскольку
 ,
, то, учитывая, что
 , запишем:
, запишем: .
.Тогда ![\sqrt[4]{\left ( \frac{3}{2} -\sqrt{2}\right )^{4}}=\frac{3}{2}-\sqrt{2} LaTeX formula: \sqrt[4]{\left ( \frac{3}{2} -\sqrt{2}\right )^{4}}=\frac{3}{2}-\sqrt{2}](/uploads/formulas/3d67e3f41623ba7f128077a01de8cc7fcce6be71.1.1.png) .
.
![\sqrt[4]{\left ( \frac{3}{2} -\sqrt{2}\right )^{4}}=\frac{3}{2}-\sqrt{2} LaTeX formula: \sqrt[4]{\left ( \frac{3}{2} -\sqrt{2}\right )^{4}}=\frac{3}{2}-\sqrt{2}](/uploads/formulas/3d67e3f41623ba7f128077a01de8cc7fcce6be71.1.1.png) .
.Упростим выражение: ![\sqrt[5]{(1-\sqrt{2})^{5}}=1-\sqrt{2} LaTeX formula: \sqrt[5]{(1-\sqrt{2})^{5}}=1-\sqrt{2}](/uploads/formulas/08a9b4b2750614dad90e9f42752f16900e518a26.2.1.png) .
.
![\sqrt[5]{(1-\sqrt{2})^{5}}=1-\sqrt{2} LaTeX formula: \sqrt[5]{(1-\sqrt{2})^{5}}=1-\sqrt{2}](/uploads/formulas/08a9b4b2750614dad90e9f42752f16900e518a26.2.1.png) .
.Найдем значение данного выражения, упрощая его и применяя формулу 1.10:

 .
. Ответ: 16.
Все преобразования иррационального выражения выполняем только в области его определения (в области допустимых значений).


![\sqrt{3\sqrt{2x}-2\sqrt{3x}}=\sqrt[4]{\left ( 3\sqrt{2x}-2\sqrt{3x} \right )^{2}}=\sqrt[4]{30x-12x\sqrt{6}} LaTeX formula: \sqrt{3\sqrt{2x}-2\sqrt{3x}}=\sqrt[4]{\left ( 3\sqrt{2x}-2\sqrt{3x} \right )^{2}}=\sqrt[4]{30x-12x\sqrt{6}}](/uploads/formulas/b6700dcc9c294aa8b137a62363245c57a4737c43.1.1.png)
![=\sqrt[4]{6x\left ( 5-2\sqrt{6} \right )} LaTeX formula: =\sqrt[4]{6x\left ( 5-2\sqrt{6} \right )}](/uploads/formulas/96da910ce69e0d213315d399ec0a4b62e15b82e5.1.1.png)




![\sqrt[n]{a}=a^{\frac{1}{n}} LaTeX formula: \sqrt[n]{a}=a^{\frac{1}{n}}](/uploads/formulas/89d296a3d4438201e22973da63abda647df30754.2.1.png) и применяя формулу
и применяя формулу