Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
, где число 
– основание степени, а число 
– показатель степени.
Н а п р и м е р:
, где 
– основание, 
– показатель степени.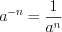 
; (1.9) 
. (1.10) 
, где 
и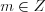 
.
Понятие степени числа
Произведение сомножителей, каждый из которых равен , называют -ной степенью числа :
сомножителей, каждый из которых равен , называют -ной степенью числа : , где число – основание степени, а число – показатель степени. Н а п р и м е р:
, где – основание, – показатель степени. Если показатель степени равен 
, то при возведении любого числа в первую степень будем получать это же число: 
.
Н а п р и м е р:
; 
.
, то при возведении любого числа в первую степень будем получать это же число: . Н а п р и м е р:
; .Для любого действительного числа , при условии, что 
, справедливо равенство 
. Выражение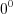 
не имеет смысла.
Н а п р и м е р:
; 
.
, при условии, что , справедливо равенство . Выражение 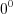не имеет смысла. Н а п р и м е р:
; .Степень с натуральным показателем 
1. При возведении в степень положительного числа будем всегда получать положительное число: если 
, то и 
.
, то и . 2. При возведении в степень отрицательного числа можем получить как положительное, так и отрицательное число:
а) если показатель степени четное число, то получим положительное число: 
, где 
;
, где ; б) если показатель степени нечетное число, то получим отрицательное число: 
, где .
, где . Например: 
; 
; 
.
; ; . Степень с целым отрицательным показателем
Для любых действительных чисел и , при условии, что и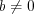 
, справедливы равенства:
и , при условии, что и 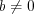, справедливы равенства: 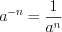; (1.9) . (1.10)Н а п р и м е р: 
; 
.
; .Свойства степеней:
1) 
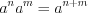; (1.11)
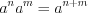; (1.11)2) 
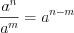; (1.12)
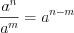; (1.12)3) 
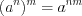; (1.13)
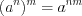; (1.13) 4) 
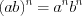; (1.14)
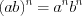; (1.14)5) 
. (1.15)
. (1.15)Свойство 1.11 формулируют так: при умножении степеней с одинаковым основанием необходимо основание степени оставить прежним, а показатели сложить.
Н а п р и м е р,
.
Н а п р и м е р,
.Свойство 1.12 формулируют так: при делении степеней с одинаковым основанием необходимо основание степени оставить прежним, а показатели вычесть.
Н а п р и м е р,
.
Н а п р и м е р,
.Свойство 1.13 формулируют так: при возведении степени в степень необходимо основание степени оставить прежним, а показатели умножить.
Н а п р и м е р,
.
Н а п р и м е р,
. Свойство 1.14 формулируют так: при возведении произведения в степень необходимо каждый множитель возвести в эту степень.
Н а п р и м е р,
.
Н а п р и м е р,
.Свойство 1.15 формулируют так: при возведении частного (дроби) в степень необходимо делимое и делитель (числитель и знаменатель дроби) возвести в эту степень.
Н а п р и м е р,
.
Н а п р и м е р,
. Стандартный вид числа
Стандартным видом числа 
называют запись:
называют запись:, где и 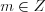.Число 
называют порядком числа.
Н а п р и м е р:
; 
.
называют порядком числа. Н а п р и м е р:
; .Если – натуральное число, то записывая числа в стандартном виде, необходимо знать, что:
– натуральное число, то записывая числа в стандартном виде, необходимо знать, что:1) 
и 
;
и ; 2) чтобы умножить число на 
, необходимо запятую перенести на цифр вправо,
н а п р и м е р,
;
, необходимо запятую перенести на цифр вправо, н а п р и м е р,
;3) чтобы разделить число на , необходимо запятую перенести на n цифр влево,
н а п р и м е р,
;
, необходимо запятую перенести на n цифр влево, н а п р и м е р,
;4) справедливо равенство 
.
. 
.
.
.
.
. 
, 
.
Выражения 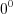и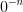 
не имеют смысла.
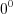и 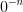не имеют смысла.