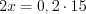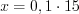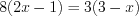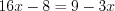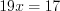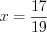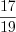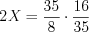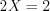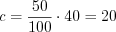Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 .
.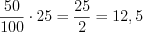 .
. 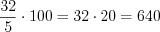 .
.  %
%  %
%  %.
%.
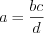 ;
;  ;
; 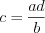 ;
;  .
.
Частное от деления одного числа на другое называют
их отношением.
Два равных отношения образуют пропорцию.
Два равных отношения образуют пропорцию.
Н а п р и м е р, 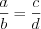 – пропорция, где
– пропорция, где  и
и  – крайние,
– крайние,  и
и  – средние члены этой пропорции.
– средние члены этой пропорции.
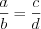 – пропорция, где
– пропорция, где  и
и  – крайние,
– крайние,  и
и  – средние члены этой пропорции.
– средние члены этой пропорции.Основное свойство пропорции
Произведение средних членов пропорции равно произведению ее крайних членов:
если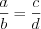 , то
, то 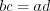 . (1.5)
. (1.5)
Произведение средних членов пропорции равно произведению ее крайних членов:
если
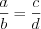 , то
, то 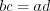 . (1.5)
. (1.5)Две взаимно зависимые величины называются пропорциональными, если отношение их значений остается неизменным.
Неизменное отношение пропорциональных величин называют коэффициентом пропорциональности и обозначают .
.
Неизменное отношение пропорциональных величин называют коэффициентом пропорциональности и обозначают
 .
. Н а п р и м е р, 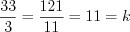 .
.
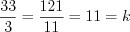 .
. Процентом числа называют одну сотую часть этого числа:
 % от числа
% от числа  равен
равен  .
.
 % от числа
% от числа  равен
равен  .
.Задачи на проценты
1. Нахождение процента от числа:
 % от числа
% от числа  равны
равны  . (1.6)
. (1.6)
 % от числа
% от числа  равны
равны  . (1.6)
. (1.6)2. Нахождение числа по его проценту:
если % от некоторого числа равны
% от некоторого числа равны  , то это число равно
, то это число равно  . (1.7)
. (1.7)
если
 % от некоторого числа равны
% от некоторого числа равны  , то это число равно
, то это число равно  . (1.7)
. (1.7)3. Нахождение процентного отношения чисел:
процентное отношение числа к числу
к числу  равно
равно  %. (1.8)
%. (1.8)
процентное отношение числа
 к числу
к числу  равно
равно  %. (1.8)
%. (1.8)Пример 1. Решите пропорцию 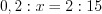 .
.
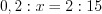 .
. Пример 2. Решите пропорцию 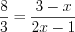 .
.
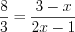 .
.Пример 3. Найдите  из пропорции
из пропорции  .
.
 из пропорции
из пропорции  .
. Решение.Найдем значение выражения, стоящего в числителе
первой дроби:
1)  ;
;
 ;
;2) 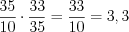 ;
;
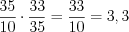 ;
;3)  ;
;
 ;
;4)  .
.
 .
.Найдем
значение выражения, стоящего в числителе второй дроби:
5) 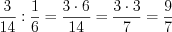 ;
;
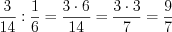 ;
;6) 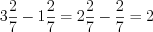 .
.
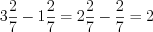 .
.Найдем
значение выражения, стоящего в знаменателе второй дроби:
7) 
 .
.Запишем пропорцию  .
.
 .
. Ответ:  .
.
 .
.Пример 4. Найдите  % от числа
% от числа  .
.
 % от числа
% от числа  .
.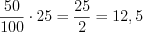 .
.Ответ:  .
.
 .
.Пример 5. Найдите число,  % которого равны
% которого равны 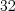 .
.
 % которого равны
% которого равны 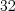 .
.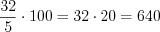 .
. Ответ:  .
.
 .
.Пример 6. Найдите процентное отношение чисел 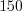 и
и 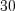 .
.
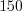 и
и 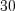 .
.  %
%  %
%  %.
%.Ответ:  %.
%.
 %.
%.Пример 7. Число  и составляет
и составляет 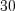 % от числа
% от числа  . Число
. Число  составляет
составляет  % от числа
% от числа  . Во сколько раз процентное отношение чисел
. Во сколько раз процентное отношение чисел  и
и  больше процентного отношения чисел
больше процентного отношения чисел  и
и  ?
?
 и составляет
и составляет 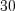 % от числа
% от числа  . Число
. Число  составляет
составляет  % от числа
% от числа  . Во сколько раз процентное отношение чисел
. Во сколько раз процентное отношение чисел  и
и  больше процентного отношения чисел
больше процентного отношения чисел  и
и  ?
? 4. Найдем процентное отношение числа  к числу
к числу  :
:
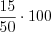 %
% 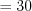 %.
%.
 к числу
к числу  :
: 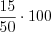 %
% 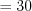 %.
%.5. Найдем во сколько раз процентное отношение чисел  и
и  больше процентного отношения чисел
больше процентного отношения чисел  и
и  :
:
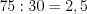 .
.
 и
и  больше процентного отношения чисел
больше процентного отношения чисел  и
и  :
: 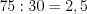 .
.Ответ: в  раза.
раза.
Неизвестные члены пропорции 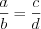 можно найти так:
можно найти так:
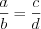 можно найти так:
можно найти так: 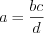 ;
;  ;
; 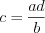 ;
;  .
.

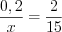 .
.