Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты








 .
.
Число (5) рациональное, значит, исключим варианты ответов, не содержащие этого числа, то есть варианты г) и д).
Рациональными числами называют числа, которые можно представить в виде обыкновенной дроби  , где
, где 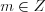 и
и  .
.
Множество рациональных чисел обозначают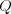 .
.
 , где
, где 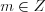 и
и  .
. Множество рациональных чисел обозначают
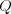 .
. Рациональными являются натуральные и целые числа, а также конечные и периодические десятичные дроби, так как все они могут быть обращены в обыкновенную дробь.
Множество иррациональных чисел состоит из бесконечных непериодических десятичных дробей.
Н а п р и м е р, иррациональными являются числа: ;
;  ;
;  .
.
Н а п р и м е р, иррациональными являются числа:
 ;
;  ;
;  .
.Все рациональные и все иррациональные числа образуют множество действительных чисел.
Запись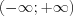 обозначает множество всех действительных чисел
обозначает множество всех действительных чисел  или множество всех точек числовой прямой.
или множество всех точек числовой прямой.
Запись
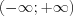 обозначает множество всех действительных чисел
обозначает множество всех действительных чисел  или множество всех точек числовой прямой.
или множество всех точек числовой прямой.Координаты точек
Рассмотрим прямую, на которой указаны начало отсчета, положительное направление и единичный отрезок. Каждой точке этой прямой соответствует число, которое называют координатой точки на прямой.
Н а п р и м е р, на рисунке 1.4 точка  имеет координату
имеет координату 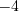 , точка
, точка  – координату
– координату  , а точка
, а точка  – координату
– координату  . Записывают:
. Записывают:  ,
,  ,
,  .
.
 имеет координату
имеет координату 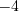 , точка
, точка  – координату
– координату  , а точка
, а точка  – координату
– координату  . Записывают:
. Записывают:  ,
,  ,
,  .
.
Расположим две координатные прямые  и
и  так, чтобы они пересекались под прямым углом (рис. 1.5). Говорят, что на плоскости задана прямоугольная декартова система координат.
так, чтобы они пересекались под прямым углом (рис. 1.5). Говорят, что на плоскости задана прямоугольная декартова система координат.
Прямую называют осью абсцисс, а прямую
называют осью абсцисс, а прямую  – осью ординат.
– осью ординат.
Эти прямые (координатные оси) делят плоскость на четыре части, которые называют ,
,  ,
,  и
и  координатными четвертями.
координатными четвертями.
 и
и  так, чтобы они пересекались под прямым углом (рис. 1.5). Говорят, что на плоскости задана прямоугольная декартова система координат.
так, чтобы они пересекались под прямым углом (рис. 1.5). Говорят, что на плоскости задана прямоугольная декартова система координат. Прямую
 называют осью абсцисс, а прямую
называют осью абсцисс, а прямую  – осью ординат.
– осью ординат. Эти прямые (координатные оси) делят плоскость на четыре части, которые называют
 ,
,  ,
,  и
и  координатными четвертями.
координатными четвертями. Каждой точке координатной плоскости соответствует пара чисел 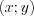 , которые называют координатами точки на плоскости.
, которые называют координатами точки на плоскости.
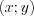 , которые называют координатами точки на плоскости.
, которые называют координатами точки на плоскости.Н а п р и м е р, на координатной плоскости (рис. 1.6) построим точку  с координатами
с координатами  и
и  .
.
Для этого отложим на оси
 единичных отрезка вправо и через эту точку проведем прямую, параллельную оси
единичных отрезка вправо и через эту точку проведем прямую, параллельную оси  . Отложим на оси
. Отложим на оси 
 единичных отрезка вверх и через эту точку проведем прямую, параллельную оси
единичных отрезка вверх и через эту точку проведем прямую, параллельную оси  . В результате пересечения этих прямых получим точку
. В результате пересечения этих прямых получим точку  , которой соответствуют два числа: число
, которой соответствуют два числа: число  – абсцисса точки
– абсцисса точки  , число
, число –ордината точки
–ордината точки  . Запишем:
. Запишем: 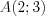 .
.
 с координатами
с координатами  и
и  .
. Для этого отложим на оси

 единичных отрезка вправо и через эту точку проведем прямую, параллельную оси
единичных отрезка вправо и через эту точку проведем прямую, параллельную оси  . Отложим на оси
. Отложим на оси 
 единичных отрезка вверх и через эту точку проведем прямую, параллельную оси
единичных отрезка вверх и через эту точку проведем прямую, параллельную оси  . В результате пересечения этих прямых получим точку
. В результате пересечения этих прямых получим точку  , которой соответствуют два числа: число
, которой соответствуют два числа: число  – абсцисса точки
– абсцисса точки  , число
, число –ордината точки
–ордината точки  . Запишем:
. Запишем: 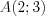 .
. Изображения числовых множеств
Отрезок ![[a;b] LaTeX formula: [a;b]](/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  .
.
С другой стороны это множество точек числовой прямой, состоящее из точек и
и  , а также всех точек, находящихся между ними (рис. 1.7).
, а также всех точек, находящихся между ними (рис. 1.7).
![[a;b] LaTeX formula: [a;b]](/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  .
. С другой стороны это множество точек числовой прямой, состоящее из точек
 и
и  , а также всех точек, находящихся между ними (рис. 1.7).
, а также всех точек, находящихся между ними (рис. 1.7). Н а п р и м е р, на рисунке 1.8 отрезок ![[-2;3] LaTeX formula: [-2;3]](/uploads/formulas/dfcbf46c84a86a603bdc915d3b104328ef1d5d27.1.1.png) есть множество всех действительных чисел, удовлетворяющих неравенству
есть множество всех действительных чисел, удовлетворяющих неравенству  .
.
![[-2;3] LaTeX formula: [-2;3]](/uploads/formulas/dfcbf46c84a86a603bdc915d3b104328ef1d5d27.1.1.png) есть множество всех действительных чисел, удовлетворяющих неравенству
есть множество всех действительных чисел, удовлетворяющих неравенству  .
.
Интервал  – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  .
.
Если из отрезка![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) исключить точки
исключить точки  и
и  , то получим интервал
, то получим интервал  (рис. 1.9).
(рис. 1.9).
 – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  .
.Если из отрезка
![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) исключить точки
исключить точки  и
и  , то получим интервал
, то получим интервал  (рис. 1.9).
(рис. 1.9).
Н а п р и м е р, на рисунке 1.10 интервал  есть множество всех действительных чисел, удовлетворяющих неравенству
есть множество всех действительных чисел, удовлетворяющих неравенству  .
.
 есть множество всех действительных чисел, удовлетворяющих неравенству
есть множество всех действительных чисел, удовлетворяющих неравенству  .
.Полуинтервалы  и
и ![(a;b] LaTeX formula: (a;b]](/uploads/formulas/052ddd32d10a911045eafff92571f5a412c5585f.1.1.png) – множества всех действительных чисел, удовлетворяющих неравенствам
– множества всех действительных чисел, удовлетворяющих неравенствам  и
и  .
.
 и
и ![(a;b] LaTeX formula: (a;b]](/uploads/formulas/052ddd32d10a911045eafff92571f5a412c5585f.1.1.png) – множества всех действительных чисел, удовлетворяющих неравенствам
– множества всех действительных чисел, удовлетворяющих неравенствам  и
и  .
.Н а п р и м е р, полуинтервал  – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  (рис. 1.11), а полуинтервал
(рис. 1.11), а полуинтервал ![(-3;0] LaTeX formula: (-3;0]](/uploads/formulas/b5ccda90157f5b5807010c857a693b368b1613d4.1.1.png) – множество всех действительных чисел, удовлетворяющих неравенству
– множество всех действительных чисел, удовлетворяющих неравенству  (рис. 1.12).
(рис. 1.12).
 – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  (рис. 1.11), а полуинтервал
(рис. 1.11), а полуинтервал ![(-3;0] LaTeX formula: (-3;0]](/uploads/formulas/b5ccda90157f5b5807010c857a693b368b1613d4.1.1.png) – множество всех действительных чисел, удовлетворяющих неравенству
– множество всех действительных чисел, удовлетворяющих неравенству  (рис. 1.12).
(рис. 1.12).
Отрезки, интервалы и полуинтервалы называют промежутками.
Длина отрезка. Чтобы найти длину отрезка, необходимо из координаты конца отрезка вычесть координату его начала, то есть длина отрезка ![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) равна
равна  .
.
![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) равна
равна  .
. Середина отрезка. Чтобы найти середину отрезка, необходимо найти полусумму координат концов отрезка, то есть серединой отрезка ![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) является число
является число  .
.
![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) является число
является число  .
.Операции над числовыми множествами
Запись  означает, что имеем
означает, что имеем  -элементное множество
-элементное множество  , состоящее из элементов
, состоящее из элементов  . Так как каждый из этих элементов принадлежит множеству
. Так как каждый из этих элементов принадлежит множеству  , то записывают:
, то записывают:  ,
,  и т. д. Если некоторый элемент
и т. д. Если некоторый элемент  не принадлежит заданному множеству
не принадлежит заданному множеству  , то записывают:
, то записывают:  .
.
 означает, что имеем
означает, что имеем  -элементное множество
-элементное множество  , состоящее из элементов
, состоящее из элементов  . Так как каждый из этих элементов принадлежит множеству
. Так как каждый из этих элементов принадлежит множеству  , то записывают:
, то записывают:  ,
,  и т. д. Если некоторый элемент
и т. д. Если некоторый элемент  не принадлежит заданному множеству
не принадлежит заданному множеству  , то записывают:
, то записывают:  .
.Н а п р и м е р, запишем, что число  принадлежит множеству целых чисел, но не принадлежит множеству натуральных чисел:
принадлежит множеству целых чисел, но не принадлежит множеству натуральных чисел:  ,
,  .
.
 принадлежит множеству целых чисел, но не принадлежит множеству натуральных чисел:
принадлежит множеству целых чисел, но не принадлежит множеству натуральных чисел:  ,
,  .
.Множество  является подмножеством множества
является подмножеством множества  , если все элементы множества
, если все элементы множества  являются элементами множества
являются элементами множества  . Говорят, что множество
. Говорят, что множество  содержит в себе множество
содержит в себе множество  или, что множество
или, что множество  включается в множество
включается в множество  и записывают:
и записывают:  .
.
 является подмножеством множества
является подмножеством множества  , если все элементы множества
, если все элементы множества  являются элементами множества
являются элементами множества  . Говорят, что множество
. Говорят, что множество  содержит в себе множество
содержит в себе множество  или, что множество
или, что множество  включается в множество
включается в множество  и записывают:
и записывают:  .
. Например, множество натуральных чисел является подмножеством множества рациональных чисел, а множество рациональных чисел – подмножеством множества действительных чисел:  и
и  .
.
 и
и  .
.Объединением двух множеств  и
и  называют множество
называют множество  , состоящее из элементов, принадлежащих хотя бы одному из множеств
, состоящее из элементов, принадлежащих хотя бы одному из множеств  или
или  . Объединение множеств
. Объединение множеств  и
и  записывают так:
записывают так:  .
.
 и
и  называют множество
называют множество  , состоящее из элементов, принадлежащих хотя бы одному из множеств
, состоящее из элементов, принадлежащих хотя бы одному из множеств  или
или  . Объединение множеств
. Объединение множеств  и
и  записывают так:
записывают так:  .
.Примером объединения множеств является решение совокупности неравенств: решением совокупности неравенств  является объединение промежутков
является объединение промежутков  и
и  .
.
 является объединение промежутков
является объединение промежутков  и
и  .
. Пересечением двух множеств  и
и  называют множество
называют множество  , состоящее из элементов, принадлежащих и множеству
, состоящее из элементов, принадлежащих и множеству  и множеству
и множеству  . Пересечение множеств
. Пересечение множеств  и
и  записывают так:
записывают так:  . Если множества
. Если множества  и
и  не содержат общих элементов, то их пересечение пусто:
не содержат общих элементов, то их пересечение пусто:  .
.
 и
и  называют множество
называют множество  , состоящее из элементов, принадлежащих и множеству
, состоящее из элементов, принадлежащих и множеству  и множеству
и множеству  . Пересечение множеств
. Пересечение множеств  и
и  записывают так:
записывают так:  . Если множества
. Если множества  и
и  не содержат общих элементов, то их пересечение пусто:
не содержат общих элементов, то их пересечение пусто:  .
.Примером пересечения множеств является решение системы неравенств:
решением системы неравенств является пересечение промежутков
является пересечение промежутков  и
и  .
.
решением системы неравенств
 является пересечение промежутков
является пересечение промежутков  и
и  .
. Пример 1. Найдите длину и середину отрезка ![[-4;8] LaTeX formula: [-4;8]](/uploads/formulas/96b99006963c900b1ca5f0ad7d79b7bd3952a7cd.1.1.png) .
.
![[-4;8] LaTeX formula: [-4;8]](/uploads/formulas/96b99006963c900b1ca5f0ad7d79b7bd3952a7cd.1.1.png) .
.Решение. Длина отрезка равна:  .
.
 .
.Середина отрезка равна:  .
.
 .
.Ответ:  ;
;  .
.
 ;
;  .
.Пример 2. Решите  и
и  .
.
 и
и  .
.Решение. Решением совокупности неравенств  является объединение промежутков:
является объединение промежутков:
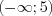 и
и  (рис. 1.13). Запишем:
(рис. 1.13). Запишем:  .
.
 является объединение промежутков:
является объединение промежутков: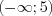 и
и  (рис. 1.13). Запишем:
(рис. 1.13). Запишем:  .
.
Решение системы неравенств  показано на рисунке 1.14 – это промежуток
показано на рисунке 1.14 – это промежуток  .
.
Ответ: .
.
 показано на рисунке 1.14 – это промежуток
показано на рисунке 1.14 – это промежуток  .
. Ответ:
 .
.Пример 3. Вычислите  .
.
 .
.Решение. Найдем значение выражения, записанного в числителе дроби:
1)  ;
;
 ;
;2)  ;
;
 ;
;3)  .
.
 .
.Найдем значение выражения, записанного в знаменателе дроби:
4)  ;
;
 ;
;5)  ;
;
 ;
;6)  ;
;
 ;
;7) 
 ;
;

 ;
;8)  .
.
 .
.Разделим числитель дроби на ее знаменатель:
 .
.
Ответ: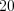 .
.
 .
. Ответ:
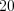 .
.Пример 4. Найдите сумму всех чисел  , каждое из которых делится без остатка на
, каждое из которых делится без остатка на  и принадлежит промежутку
и принадлежит промежутку  .
.
 , каждое из которых делится без остатка на
, каждое из которых делится без остатка на  и принадлежит промежутку
и принадлежит промежутку  .
.Решение. Рассмотрим отрезок ![[-252;252] LaTeX formula: [-252;252]](/uploads/formulas/2406bab69a4fe4af7d119b19c5b46b3e00bab2e1.1.1.png) и интервал
и интервал  (рис. 1.15).
(рис. 1.15).
![[-252;252] LaTeX formula: [-252;252]](/uploads/formulas/2406bab69a4fe4af7d119b19c5b46b3e00bab2e1.1.1.png) и интервал
и интервал  (рис. 1.15).
(рис. 1.15). 
1. Рассмотрим отрезок ![[-252;252] LaTeX formula: [-252;252]](http://helpy.quali.me/uploads/formulas/2406bab69a4fe4af7d119b19c5b46b3e00bab2e1.1.1.png) .
.
Сумма всех чисел, каждое из которых делится без остатка на и принадлежит этому отрезку, будет равна нулю:
и принадлежит этому отрезку, будет равна нулю:
( ,
,  и т. д.).
и т. д.).
![[-252;252] LaTeX formula: [-252;252]](http://helpy.quali.me/uploads/formulas/2406bab69a4fe4af7d119b19c5b46b3e00bab2e1.1.1.png) .
. Сумма всех чисел, каждое из которых делится без остатка на
 и принадлежит этому отрезку, будет равна нулю:
и принадлежит этому отрезку, будет равна нулю:(
 ,
,  и т. д.).
и т. д.).2. Рассмотрим интервал  .
.
Зная, что число делится на
делится на , но не принадлежит рассматриваемому интервалу, найдем все числа, кратные
, но не принадлежит рассматриваемому интервалу, найдем все числа, кратные  и не превосходящие число
и не превосходящие число  .
.
Получим: ,
,  .
.
 .
. Зная, что число
 делится на
делится на , но не принадлежит рассматриваемому интервалу, найдем все числа, кратные
, но не принадлежит рассматриваемому интервалу, найдем все числа, кратные  и не превосходящие число
и не превосходящие число  .
. Получим:
 ,
,  .
. 3. Тогда  .
.
 .
.Ответ:  .
.
 .
.Пример 5. Укажите все номера рациональных чисел данного множества:
![\sqrt[3]{32\sqrt[4]{2}}\cdot 2^{1/4} LaTeX formula: \sqrt[3]{32\sqrt[4]{2}}\cdot 2^{1/4}](/uploads/formulas/a4b55642f3767b50a31584a23ecbdc6fc5bd6270.1.1.png) (1);
(1);  (2);
(2);  (3);
(3);  (4);
(4);  (5).
(5).
![\sqrt[3]{32\sqrt[4]{2}}\cdot 2^{1/4} LaTeX formula: \sqrt[3]{32\sqrt[4]{2}}\cdot 2^{1/4}](/uploads/formulas/a4b55642f3767b50a31584a23ecbdc6fc5bd6270.1.1.png) (1);
(1);  (2);
(2);  (3);
(3);  (4);
(4);  (5).
(5).Варианты ответов: а)  ,
, ,
,  ; б)
; б)  ,
,  ,
,  ; в)
; в)  ,
,  ,
,  ; г)
; г)  ,
,  ,
,  ; д)
; д)  ,
,  ,
,  .
.
 ,
, ,
,  ; б)
; б)  ,
,  ,
,  ; в)
; в)  ,
,  ,
,  ; г)
; г)  ,
,  ,
,  ; д)
; д)  ,
,  ,
,  .
.Решение. Применим метод исключений, выполняя следующие преобразования.
1. Преобразуем любое число данного множества, например число (5):


 .
. Число (5) рациональное, значит, исключим варианты ответов, не содержащие этого числа, то есть варианты г) и д).
2. Преобразуем число (3):
 .
.
Число (3) иррациональное, значит, исключим вариант ответа в).
 .
. Число (3) иррациональное, значит, исключим вариант ответа в).
3. Преобразуем любое из чисел (2) или (4), так как число (1) входит в оба оставшихся варианта ответа:
 . Число (4) - рациональное.
. Число (4) - рациональное.
 . Число (4) - рациональное.
. Число (4) - рациональное.Ответ: б.
1. Обозначения числовых множеств:
1)  – множество натуральных чисел;
– множество натуральных чисел;
 – множество натуральных чисел;
– множество натуральных чисел;2) 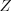 – множество целых чисел;
– множество целых чисел;
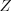 – множество целых чисел;
– множество целых чисел;3) 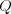 – множество рациональных чисел;
– множество рациональных чисел;
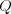 – множество рациональных чисел;
– множество рациональных чисел;4)  – множество иррациональных чисел;
– множество иррациональных чисел;
 – множество иррациональных чисел;
– множество иррациональных чисел;5)  – множество действительных чисел;
– множество действительных чисел;
 – множество действительных чисел;
– множество действительных чисел;6) 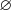 – пустое множество.
– пустое множество.
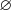 – пустое множество.
– пустое множество.2. Справедливо, что:  ;
;  ;
;  .
.
 ;
;  ;
;  .
. 
