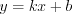 , где
, где  и
и  – действительные числа.
– действительные числа. Число
 называют угловым коэффициентом прямой.
называют угловым коэффициентом прямой. Графиком линейной функции является прямая (рис. 2.11 – 2.13).
 , то функция монотонно возрастает (рис. 2.11).
, то функция монотонно возрастает (рис. 2.11).  , то функция монотонно убывает (рис. 2.12).
, то функция монотонно убывает (рис. 2.12).  , то функция примет вид
, то функция примет вид 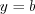 .
. Придавая
 произвольные значения, получим семейство прямых параллельных оси
произвольные значения, получим семейство прямых параллельных оси  (рис. 2.13).
(рис. 2.13).  , то функция примет вид
, то функция примет вид  .
. Такую функциональную зависимость называют прямой пропорциональностью.
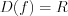 .
. Область значений линейной функции
 .
.  прямой
прямой 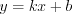 находят по
формуле
находят по
формуле
 ,
, где
 – угол наклона прямой к положительному направлению оси
– угол наклона прямой к положительному направлению оси  (рис. 2.11).
(рис. 2.11).  и
и  на плоскости:
на плоскости:1) если
 , то прямые
пересекаются
;
, то прямые
пересекаются
; 2) если
 и
и 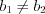 , то прямые
параллельны
;
, то прямые
параллельны
;3) если
 и
и  , то прямые
совпадают
.
, то прямые
совпадают
.Степенной
называют функцию вида  ,
,
где  – положительное действительное число, отличное от нуля.
– положительное действительное число, отличное от нуля.
Примеры степенных функций.
1. Если функция имеет вид  (рис. 2.14), то
(рис. 2.14), то  :
: 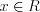 , а
, а  :
:  .
.
2. Если функция имеет вид  (рис. 2.15), то
(рис. 2.15), то 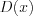 :
: 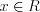 , а
, а 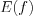 :
:  .
.
3. Если функция имеет вид 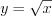 (рис. 2.16), то
(рис. 2.16), то  :
:  , а
, а 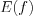 :
:  .
.
4. Если функция имеет вид ![y=\sqrt[3]{x} LaTeX formula: y=\sqrt[3]{x}](/uploads/formulas/f8c1b58cafb804617a8eaf711b449e103ca70482.1.1.png) (рис. 2.17), то
(рис. 2.17), то  :
: 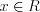 , а
, а 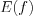 :
:  .
.
5. Если функция имеет вид  , где
, где  – отличное от нуля действительное число (рис. 2.18, 2.19), то
– отличное от нуля действительное число (рис. 2.18, 2.19), то
 :
:  , а
, а 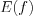 :
:  .
.
Функцию  называют
обратной пропорциональностью.
называют
обратной пропорциональностью.
Если  , то ее график расположен в первой и третьей четвертях координатной плоскости (рис.2.18).
, то ее график расположен в первой и третьей четвертях координатной плоскости (рис.2.18).
Если  , то – во второй и четвертой четвертях координатной плоскости (рис. 2.19).
, то – во второй и четвертой четвертях координатной плоскости (рис. 2.19).
6. Если функция имеет вид  (рис. 2.20), то
(рис. 2.20), то  :
:  , а
, а 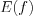 :
:  .
.
Квадратичная функция
Квадратичной
называют функцию вида  ,
,
где  ,
,  ,
,  – действительные числа (
– действительные числа ( ) .
) .
График квадратичной функции называется
параболой.
Координаты вершины  параболы находят по формулам:
параболы находят по формулам:
 ,
,  .
.
Прямая  –
ось симметрии
параболы.
–
ось симметрии
параболы.
 на координатной плоскости зависит от значения дискриминанта
на координатной плоскости зависит от значения дискриминанта  и знака коэффициента
и знака коэффициента  .
. Возможны следующие случаи:
1)
 и
и 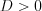 (рис. 2.21);
(рис. 2.21); 2)
 и
и 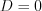 (рис. 2.22);
(рис. 2.22); 3)
 и
и  (рис. 2.23);
(рис. 2.23); и
и 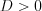 (рис. 2.24);
(рис. 2.24); 5)
 и
и 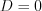 (рис. 2.25);
(рис. 2.25); 6)
 и
и  (рис. 2.26).
(рис. 2.26). наименьшим значением функции является ордината вершины параболы и
наименьшим значением функции является ордината вершины параболы и  .
.  наибольшим значением функции является ордината вершины параболы и
наибольшим значением функции является ордината вершины параболы и ![E(f)=(-\infty ;y_{0}] LaTeX formula: E(f)=(-\infty ;y_{0}]](/uploads/formulas/20cbb66e69c98805f201ef5244fdeb47bea759a9.1.1.png) .
. 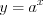 ,
, где
 и
и  .
. Если
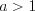 , то функция монотонно возрастает (рис. 2.27).
, то функция монотонно возрастает (рис. 2.27). Если
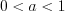 , то функция монотонно убывает (рис. 2.28).
, то функция монотонно убывает (рис. 2.28). :
: 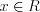 . Область значений
. Область значений 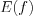 :
:  .
. 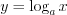 , где
, где  и
и  .
. Если основание логарифма
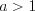 , то функция монотонно возрастает (рис. 2.29).
, то функция монотонно возрастает (рис. 2.29).Если
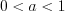 , то функция монотонно убывает (рис. 2.30).
, то функция монотонно убывает (рис. 2.30).  . Область значений
. Область значений 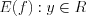 .
.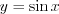 ,
, 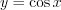 ,
,  и
и 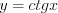 .
. 1. Если функция имеет вид
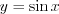 (рис.2.31), то
(рис.2.31), то  :
: 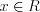 ,
, 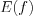 :
: ![y\in [-1;1] LaTeX formula: y\in [-1;1]](/uploads/formulas/f60d17e426fb9053ba17362774d52aa31ef31d31.1.1.png) ; основной период
; основной период  .
.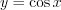 (рис. 2.32), то
(рис. 2.32), то :
: 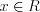 ,
, 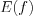 :
: ![y\in [-1;1] LaTeX formula: y\in [-1;1]](/uploads/formulas/f60d17e426fb9053ba17362774d52aa31ef31d31.1.1.png) ; основной период
; основной период  .
.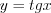 (рис. 2.33), то
(рис. 2.33), то :
: 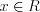 и
и  , где
, где  ;
; 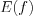 :
:  ; основной период
; основной период  .
.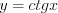 (рис. 2.34), то
(рис. 2.34), то :
: 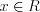 и
и  , где
, где  ;
; 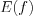 :
:  ; основной период
; основной период  .
. , то ее основной период находят по формуле:
, то ее основной период находят по формуле:  , где
, где  – основной период функции
– основной период функции  .
.  ,
,  ,
,  и
и  .
. 1) для функции
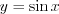 обратная функция
обратная функция  определена только на отрезке
определена только на отрезке ![\left [ -\frac{\pi }{2} ;\frac{\pi }{2}\right ] LaTeX formula: \left [ -\frac{\pi }{2} ;\frac{\pi }{2}\right ]](/uploads/formulas/96a49027adfcaf5cc0f85752b00acd00a08bbf58.1.1.png) ;
; 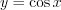 обратная функция
обратная функция  определена только на отрезке
определена только на отрезке ![\left [ 0;\pi ] LaTeX formula: \left [ 0;\pi ]](/uploads/formulas/ad3ecbe0baa5b523199f0b81e6c74227005b4660.1.1.png) ;
;  обратная функция
обратная функция  определена только на интервале
определена только на интервале  ;
; 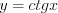 обратная функция
обратная функция  определена на интервале
определена на интервале  .
. 1. Если функция имеет вид
 (рис. 2.35), то
(рис. 2.35), то  :
: ![x\in [-1;1] LaTeX formula: x\in [-1;1]](/uploads/formulas/8dc88849028ecc07f6fd9cd49c35c436712b3757.1.1.png) ,
, 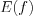 :
: ![y\in \left [-\frac{\pi }{2};\frac{\pi }{2} \right ] LaTeX formula: y\in \left [-\frac{\pi }{2};\frac{\pi }{2} \right ]](/uploads/formulas/5e8db1dc97483c080b56d86e78d9c36373b126e0.1.1.png) .
. (рис. 2.36), то
(рис. 2.36), то :
: ![x\in [-1;1 ] LaTeX formula: x\in [-1;1 ]](/uploads/formulas/318f323b48a0b0ca7dfbc8a79bc72da4aef644bc.1.1.png) ,
, 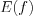 :
: ![y\in [0;\pi ] LaTeX formula: y\in [0;\pi ]](/uploads/formulas/ad2baee35e5490968eb444d9fec085352c28fceb.1.1.png) .
.  (рис. 2.37), то
(рис. 2.37), то :
: 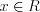 ,
, 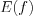 :
:  .
. (рис. 2.38), то
(рис. 2.38), то  :
: 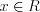 ,
, 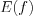 :
:  .
. , при которых наибольшее значение функции
, при которых наибольшее значение функции  равно
равно  .
. .
. Имеем квадратичную функцию, графиком корой является парабола.
Свое наибольшее значение квадратичная функция принимает в точке, которая является вершиной параболы, при условии, что ветви этой параболы направлены вниз, то есть, при условии, что
 .
. и
и  найдем координаты вершины параболы:
найдем координаты вершины параболы: ,
, ,
,  .
. , то
, то  ,
,  , откуда
, откуда  ,
,  .
. Учитывая, что
 , получим
, получим  .
. Ответ:
 .
. , при которых вершина параболы
, при которых вершина параболы  находится во второй четверти координатной плоскости.
находится во второй четверти координатной плоскости. , то запишем координаты вершины параболы:
, то запишем координаты вершины параболы:  ,
,  .
. и
и  .
. Тогда


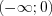 , то решим второе неравенство системы на этом промежутке методом интервалов.
, то решим второе неравенство системы на этом промежутке методом интервалов. .
. .
. Получим:
 ,
,  .
. 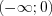 и определим знаки ее значений на полученных промежутках (рис. 2.39).
и определим знаки ее значений на полученных промежутках (рис. 2.39). .
. Этому интервалу принадлежит два целых числа
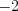 и
и  , произведение которых равно
, произведение которых равно  .
. Ответ:
 .
. ,
,  ,
,  и т. п.
и т. п.
