Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (8.18)
. (8.18) ; (8.19)
; (8.19)
 (8.20)
(8.20)
 (8.21)
(8.21)
 (8.22)
(8.22)  . (8.23)
. (8.23) и
и 
 (8.24)
(8.24)  и
и 
 (8.25)
(8.25) и
и 
 (8.26)
(8.26)  и
и 
 (8.27)
(8.27)  и
и  ,
,
 (8.28)
(8.28)
 (8.29)
(8.29)
 (8.30)
(8.30)  . (8.31)
. (8.31)
 .
.
1. Однородное линейное уравнение второго порядка с постоянными коэффициентами имеет вид:
 . (8.18)
. (8.18)Чтобы решить уравнение 8.18, необходимо:
1) составить и решить характеристическое уравнение
 ; (8.19)
; (8.19)2) записать общее решение уравнения по одной из формул:
Корни характеристического уравнения Общее решение уравнения 8.18

 (8.20)
(8.20)
 (8.21)
(8.21)
 (8.22)
(8.22)2. Неоднородное линейное уравнение второго порядка с постоянными коэффициентами имеет вид:
 . (8.23)
. (8.23)Различают частное решение и общее решение уравнения 8.23.
Частное решение  с неопределенными коэффициентами уравнения 8.23 находят по одной из формул 8.24 , 8.25 , 8.26 , 8.27 , 8.28 , 8.29 , 8.30 , где
с неопределенными коэффициентами уравнения 8.23 находят по одной из формул 8.24 , 8.25 , 8.26 , 8.27 , 8.28 , 8.29 , 8.30 , где  ,
,  – коэффициенты уравнения,
– коэффициенты уравнения, 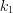 ,
, 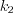 – корни характеристического уравнения
– корни характеристического уравнения  ;
;  специальная правая часть уравнения;
специальная правая часть уравнения;  ,
,  ,
,  – постоянные коэффициенты;
– постоянные коэффициенты;  ,
,  – неопределенные коэффициенты;
– неопределенные коэффициенты;  – многочлен
– многочлен  -ой степени с определенными коэффициентами;
-ой степени с определенными коэффициентами;  – многочлен
– многочлен  -ой степени с неопределенными коэффициентами:
-ой степени с неопределенными коэффициентами:
 с неопределенными коэффициентами уравнения 8.23 находят по одной из формул 8.24 , 8.25 , 8.26 , 8.27 , 8.28 , 8.29 , 8.30 , где
с неопределенными коэффициентами уравнения 8.23 находят по одной из формул 8.24 , 8.25 , 8.26 , 8.27 , 8.28 , 8.29 , 8.30 , где  ,
,  – коэффициенты уравнения,
– коэффициенты уравнения, 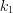 ,
, 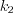 – корни характеристического уравнения
– корни характеристического уравнения  ;
;  специальная правая часть уравнения;
специальная правая часть уравнения;  ,
,  ,
,  – постоянные коэффициенты;
– постоянные коэффициенты;  ,
,  – неопределенные коэффициенты;
– неопределенные коэффициенты;  – многочлен
– многочлен  -ой степени с определенными коэффициентами;
-ой степени с определенными коэффициентами;  – многочлен
– многочлен  -ой степени с неопределенными коэффициентами:
-ой степени с неопределенными коэффициентами:  и
и 
 (8.24)
(8.24)  и
и 
 (8.25)
(8.25) и
и 
 (8.26)
(8.26)  и
и 
 (8.27)
(8.27)  и
и  ,
,
 (8.28)
(8.28)
 (8.29)
(8.29) и 


 (8.30)
(8.30) и  ,
, 
 ,
, 
Чтобы найти частное решение  с определенными коэффициентами, необходимо
с определенными коэффициентами, необходимо
 с определенными коэффициентами, необходимо
с определенными коэффициентами, необходимо 1) найти выражения  и
и  ;
;
 и
и  ;
;3) записать решение  с определенными коэффициентами.
с определенными коэффициентами.
 с определенными коэффициентами.
с определенными коэффициентами.Чтобы найти общее решение уравнение 8.23, необходимо:
1) найти общее решение  соответствующего ему однородного уравнения
соответствующего ему однородного уравнения  по одной из формул 8.20 , 8.21 ,8.22;
по одной из формул 8.20 , 8.21 ,8.22;
 соответствующего ему однородного уравнения
соответствующего ему однородного уравнения  по одной из формул 8.20 , 8.21 ,8.22;
по одной из формул 8.20 , 8.21 ,8.22; . (8.31)
. (8.31)Пример 1. Решите уравнение  .
.
 .
. Решение. Имеем уравнение вида 8.18. Составим и решим его характеристическое уравнение 8.19:  , откуда
, откуда  , а
, а  . Согласно формуле 8.20 запишем его общее решение:
. Согласно формуле 8.20 запишем его общее решение:  .
.
 , откуда
, откуда  , а
, а  . Согласно формуле 8.20 запишем его общее решение:
. Согласно формуле 8.20 запишем его общее решение:  .
.Пример 2. Решите уравнение  .
.
 .
. Решение. Имеем уравнение вида 8.18. Составим и решим его характеристическое уравнение 8.19:  , откуда
, откуда  . Согласно формуле 8.21 запишем его общее решение:
. Согласно формуле 8.21 запишем его общее решение:  или
или  .
.
 , откуда
, откуда  . Согласно формуле 8.21 запишем его общее решение:
. Согласно формуле 8.21 запишем его общее решение:  или
или  .
.Пример 3. Решите уравнение  .
.
 .
. Решение. Имеем уравнение вида 8.18. Составим и решим его характеристическое уравнение 8.19:  , откуда
, откуда  , где
, где  ,
,  . Согласно формуле 8.22 запишем его общее решение:
. Согласно формуле 8.22 запишем его общее решение:  или
или  .
.
 , откуда
, откуда  , где
, где  ,
,  . Согласно формуле 8.22 запишем его общее решение:
. Согласно формуле 8.22 запишем его общее решение:  или
или  .
.Пример 4. Решите уравнение  .
.
 .
.Решение. 1. Имеем уравнение вида 8.23. Найдем общее решение соответствующего однородного уравнения  . Так как
. Так как  , то
, то  ,
,  и согласно формуле 8.20
и согласно формуле 8.20  .
.
 . Так как
. Так как  , то
, то  ,
,  и согласно формуле 8.20
и согласно формуле 8.20  .
.2. Найдем частное решение данного неоднородного уравнения. Так как  и
и  , то согласно формуле 8.27,
, то согласно формуле 8.27,  , а
, а  ,
,  . Подставляя эти выражения в уравнение
. Подставляя эти выражения в уравнение  , получим:
, получим:
 и
и  , то согласно формуле 8.27,
, то согласно формуле 8.27,  , а
, а  ,
,  . Подставляя эти выражения в уравнение
. Подставляя эти выражения в уравнение  , получим:
, получим:  .
.Приравнивая коэффициенты при одинаковых степенях переменных, запишем:  ,
,  и
и  , откуда
, откуда  ,
,  и
и  .
.
 ,
,  и
и  , откуда
, откуда  ,
,  и
и  .
. Получим:  .
.
 .
.3. Согласно формуле 8.31 найдем общее решение данного неоднородного уравнения.
Ответ:  .
.
 .
.Мы рассмотрели несколько видов неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами только со специальной правой частью.


 ,
,