Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 .
.
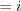 .
.
Расширим множество действительных чисел. Число, квадрат которого равен  , обозначим буквой
, обозначим буквой  и назовем его мнимой единицей. Запишем:
и назовем его мнимой единицей. Запишем:  .
. 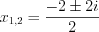 , откуда
, откуда  .
.
 .
.
 , обозначим буквой
, обозначим буквой  и назовем его мнимой единицей. Запишем:
и назовем его мнимой единицей. Запишем:  .
. Числа вида  , где
, где  и
и  – любые действительные числа, а число
– любые действительные числа, а число  – мнимая единица, называют комплексными числами.
– мнимая единица, называют комплексными числами.
 , где
, где  и
и  – любые действительные числа, а число
– любые действительные числа, а число  – мнимая единица, называют комплексными числами.
– мнимая единица, называют комплексными числами. При этом число  называют действительной частью комплексного числа, число
называют действительной частью комплексного числа, число  – его мнимой частью, а выражение
– его мнимой частью, а выражение  алгебраической формой записи комплексного числа.
алгебраической формой записи комплексного числа.
 называют действительной частью комплексного числа, число
называют действительной частью комплексного числа, число  – его мнимой частью, а выражение
– его мнимой частью, а выражение  алгебраической формой записи комплексного числа.
алгебраической формой записи комплексного числа. Множество всех комплексных чисел обозначают  .
.
 .
. Это множество содержит множество всех действительных чисел:  .
.
 .
.Например: 1) если действительная часть комплексного числа равна  , а его мнимая часть равна
, а его мнимая часть равна  , то получим комплексное число
, то получим комплексное число  ; 2) если действительная часть комплексного числа равна
; 2) если действительная часть комплексного числа равна  , а его мнимая часть равна
, а его мнимая часть равна  , то получим мнимое число
, то получим мнимое число  ; 3) если действительная часть комплексного числа равна
; 3) если действительная часть комплексного числа равна  , а его мнимая часть равна
, а его мнимая часть равна  , то получим действительное число
, то получим действительное число  .
.
 , а его мнимая часть равна
, а его мнимая часть равна  , то получим комплексное число
, то получим комплексное число  ; 2) если действительная часть комплексного числа равна
; 2) если действительная часть комплексного числа равна  , а его мнимая часть равна
, а его мнимая часть равна  , то получим мнимое число
, то получим мнимое число  ; 3) если действительная часть комплексного числа равна
; 3) если действительная часть комплексного числа равна  , а его мнимая часть равна
, а его мнимая часть равна  , то получим действительное число
, то получим действительное число  .
.Числа  и
и  называют сопряженными.
называют сопряженными.
 и
и  называют сопряженными.
называют сопряженными. Числа  и
и  называют противоположными.
называют противоположными.
 и
и  называют противоположными.
называют противоположными. Два комплексных числа  и
и  равны, если
равны, если  и
и 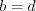 .
.
 и
и  равны, если
равны, если  и
и 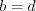 .
.Приведем примеры решений уравнений, которые не имеют действительных корней, то есть не имеют решений на множестве действительных чисел, но имеют решения на множестве комплексных чисел.
Например: 1) Решим уравнение 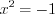 . Поскольку
. Поскольку 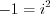 , то запишем:
, то запишем:  . Тогда
. Тогда  или
или  .
.
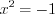 . Поскольку
. Поскольку 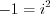 , то запишем:
, то запишем:  . Тогда
. Тогда  или
или  .
. 2) Рассмотрим квадратное уравнение  . Найдем его дискриминант:
. Найдем его дискриминант:  . Тогда
. Тогда  или
или  . Найдем комплексные корни уравнения:
. Найдем комплексные корни уравнения:
 . Найдем его дискриминант:
. Найдем его дискриминант:  . Тогда
. Тогда  или
или  . Найдем комплексные корни уравнения:
. Найдем комплексные корни уравнения: 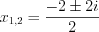 , откуда
, откуда  .
.Действия с комплексными числами
Сложение и вычитание комплексных чисел
Суммой комплексных чисел  и
и 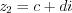 называют комплексное число
называют комплексное число  .
.
 и
и 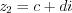 называют комплексное число
называют комплексное число  .
.Разностью комплексных чисел  и
и 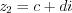 называют комплексное число
называют комплексное число  .
.
 и
и 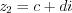 называют комплексное число
называют комплексное число  .
.Умножение комплексных чисел
Произведением комплексных чисел  и
и 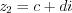 называют комплексное число
называют комплексное число  .
.
 и
и 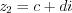 называют комплексное число
называют комплексное число  .
. Деление комплексных чисел
Комплексные числа  и
и 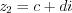 делят так:
делят так:
 и
и 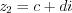 делят так:
делят так: 
 .
.Пример 1. Найдите сумму чисел  и
и 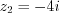 .
.
 и
и 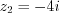 .
.Решение. 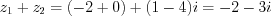 .
.
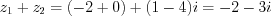 .
.Ответ:  .
.
 .
.Пример 2. Найдите произведение чисел  и
и  .
.
 и
и  .
.Решение. Применим правило умножения многочленов:
 .
.Ответ:  .
.
 .
.Пример 3. Найдите частное чисел 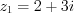 и
и  .
.
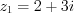 и
и  .
.Решение.

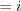 .
.Ответ:  .
.
 .
.Арифметические действия с комплексными числами в алгебраической форме выполняют по правилам действий с действительными числами, учитывая при этом, что  ,
,  ,
, 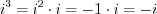 ,
,  и т. д.
и т. д.
 ,
,  ,
, 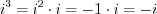 ,
,  и т. д.
и т. д.
