 является пределом числовой
последовательности
является пределом числовой
последовательности 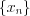 , если для любого
, если для любого  найдется такой номер
найдется такой номер , что при всех
, что при всех  выполняется неравенство
выполняется неравенство  . Записывают:
. Записывают: 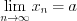 .
.
Другими словами (геометрический смысл предела): число  является пределом последовательности
является пределом последовательности 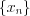 , если в любой его
, если в любой его -окрестности содержатся почти все члены последовательности или вне этой окрестности находится лишь конечное число ее членов.
-окрестности содержатся почти все члены последовательности или вне этой окрестности находится лишь конечное число ее членов.
Такая числовая последовательность называется сходящейся . Если же предел последовательности равен бесконечности или не существует, то такая числовая последовательность называется расходящейся.
Например, числовая последовательность 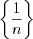 сходится и
сходится и 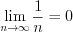 , а числовая последовательность
, а числовая последовательность  расходится.
расходится.
Числовая последовательность может быть как ограниченной так и не ограниченной. Числовая последовательность 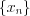 ограничена
, если
ограничена
, если  , такое, что
, такое, что 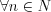 :
: .
.
Числовая последовательность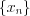 не ограничена
, если
не ограничена
, если 
 :
: .
.
Например: числовая последовательность  ограничена снизу.
ограничена снизу.
Если последовательность имеет предел, то она ограничена.
Числовая последовательность 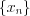 бесконечно малая
, если
бесконечно малая
, если 
 такой, что
такой, что 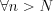 :
: .
.
Числовая последовательность 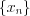 бесконечно большая , если
бесконечно большая , если 
 такой, что
такой, что  :
: . Например, последовательность
. Например, последовательность бесконечно малая, а последовательность
бесконечно малая, а последовательность  бесконечно большая.
бесконечно большая.
Число  называют
пределом функции
называют
пределом функции  в точке
в точке  , если
, если 
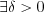 такое, что
такое, что  , выполняется неравенство
, выполняется неравенство  (рис. 5.5). Записывают:
(рис. 5.5). Записывают:  .
.
Другими словами число  называют
пределом функции
называют
пределом функции  в точке
в точке  , для любой последовательности
, для любой последовательности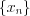 аргументов функции, сходящейся к
аргументов функции, сходящейся к  , соответствующая последовательность значений функции
, соответствующая последовательность значений функции  сходится к
сходится к  .
.


 и
правосторонний предел
и
правосторонний предел  .
. Например, на рисунке 5.6 , ,
,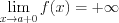 и
и 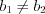 , следовательно, не существует предела функции в точке
, следовательно, не существует предела функции в точке  . На рисунке 5.7 ,
. На рисунке 5.7 , а
а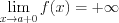 , следовательно, предела функции в точке
, следовательно, предела функции в точке  не существует.
не существует.
Свойства пределов
 ; (5.3)
; (5.3)
 ; (5.4)
; (5.4) ; (5.5)
; (5.5) ; (5.6)
; (5.6) ; (5.7)
; (5.7) ; (5.8)
; (5.8) ; (5.9)
; (5.9) 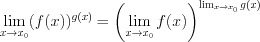 . (5.10)
. (5.10)
Равенство 5.10 справедливо, если пределы  и
и  конечны.
конечны.
Функцию  называют
бесконечно малой
в точке или в бесконечности, если ее предел равен нулю.
называют
бесконечно малой
в точке или в бесконечности, если ее предел равен нулю.
 ; (5.11)
; (5.11)Две бесконечно малые функции
 и
и  называют эквивалентными бесконечно малыми при
называют эквивалентными бесконечно малыми при  , если
, если  . (5.12)
. (5.12)Записывают:
 при
при  .
.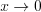
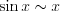 ,
,  ,
,  . (5.13)
. (5.13)При нахождении предела отношения двух бесконечно малых функций каждую из них или только одну можно заменить эквивалентной ей бесконечно малой функцией.
Функцию
 называют
бесконечно большой
в точке
называют
бесконечно большой
в точке  , если ее передел в этой точке равен бесконечности:
, если ее передел в этой точке равен бесконечности: .
.Справедливы равенства:
 ; (5.14)
; (5.14) . (5.15)
. (5.15) , если
, если 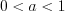 (5.16)
(5.16)  , если
, если 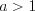 (5.17)
(5.17) , если
, если 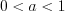 (5.18)
(5.18)  , если
, если 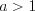 (5.19)
(5.19)Квантор
– общее название для логических операций, ограничивающих область истинности какого-либо утверждения, высказывания (предиката).
Квантор всеобщности обозначается 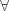 и читается: «для всех …» или «для любого …».
Квантор существования
обозначается
и читается: «для всех …» или «для любого …».
Квантор существования
обозначается  и читается: «существует …» или «найдется …». Тогда определение числовой последовательности можем записать так: число
и читается: «существует …» или «найдется …». Тогда определение числовой последовательности можем записать так: число  является пределом числовой последовательности
является пределом числовой последовательности 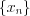 , если
, если 
 такой, что
такой, что  .
.





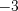 .
.