Функцией
 называют такую зависимость переменной
называют такую зависимость переменной  от переменной
от переменной  , при которой каждому допустимому значению
, при которой каждому допустимому значению соответствует
единственное значение
соответствует
единственное значение  . Переменную
. Переменную  называют независимой переменной или
аргументом функции
, а переменную
называют независимой переменной или
аргументом функции
, а переменную  – зависимой от
– зависимой от  переменной или
значением функции .
переменной или
значением функции .
Уравнение  задает функцию
явно
, а уравнение
задает функцию
явно
, а уравнение 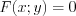 задает функцию
неявно
. Чтобы задать функцию явно, необходимо в уравнении
задает функцию
неявно
. Чтобы задать функцию явно, необходимо в уравнении 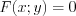 выразить одну переменную через другую.
выразить одну переменную через другую.
Множество всех допустимых значений переменной образуют
область определения
функции. Область определения функции обозначают
образуют
область определения
функции. Область определения функции обозначают  .
.
Множество всех допустимых значений переменной образуют
область значений функции
. Область значений функции обозначают
образуют
область значений функции
. Область значений функции обозначают 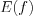 .
.
Например, область определения функции  составляют числа, принадлежащие промежутку
составляют числа, принадлежащие промежутку  , а область ее значений – числа, принадлежащие промежутку
, а область ее значений – числа, принадлежащие промежутку  .
.
Графиком функции  называют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек вида
называют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек вида 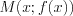 . График функции представляет собой некоторую линию на плоскости.
. График функции представляет собой некоторую линию на плоскости.
Функция  возрастает
на промежутке
возрастает
на промежутке  , если для любых
, если для любых  и
и  , принадлежащих промежутку
, принадлежащих промежутку  , из неравенства
, из неравенства 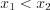 следует неравенство
следует неравенство  (рис. 5.1).
(рис. 5.1).
Функция  убывает
на промежутке
убывает
на промежутке  , если для любых
, если для любых  и
и  , принадлежащих промежутку
, принадлежащих промежутку  , из неравенства
, из неравенства  следует неравенство
следует неравенство 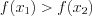 (рис. 5.2).
(рис. 5.2).
Функция называется монотонной
, если она либо только возрастает, либо только убывает на 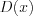 .
.

Говорят, что числовое множество симметрично
относительно точки 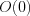 (начала отсчета) координатной прямой, если оно содержит только противоположные элементы.
(начала отсчета) координатной прямой, если оно содержит только противоположные элементы.
Например, числовые множества 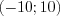 ,
, 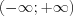 ,
,![[-3;+3] LaTeX formula: [-3;+3]](/uploads/formulas/688cc7f72274e74d5d7338263a07cfdb1573cb36.1.1.png) – симметричные, а множества
– симметричные, а множества 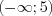 ,
,  и
и 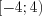 – не симметричные.
– не симметричные.
Функция
называется
четной
, если  – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и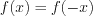 . График четной функции симметричен относительно оси
. График четной функции симметричен относительно оси  .
.
Функция
называется
нечетной
, если  – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и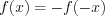 . График нечетной функции симметричен относительно точки
. График нечетной функции симметричен относительно точки  .
.
Функция  называется периодической
, если существует такое число
называется периодической
, если существует такое число 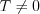 , при котором для всех
, при котором для всех  из области определения функции выполняется равенство
из области определения функции выполняется равенство 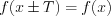 .
.
Например, тригонометрические функции 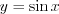 ,
, 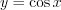 ,
, 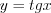 и
и 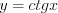 являются периодическими, так как выполняются равенства:
являются периодическими, так как выполняются равенства: 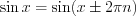 ,
,  ,
,  и
и  , где
, где  .
.
Чтобы построить график периодической функции, достаточно построить ее график на основном (наименьшем) периоде  и выполнить параллельный перенос этого графика вдоль оси абсцисс на любое количество периодов влево и вправо. Например, рассмотрим функцию
и выполнить параллельный перенос этого графика вдоль оси абсцисс на любое количество периодов влево и вправо. Например, рассмотрим функцию  . Заметим, что запись
. Заметим, что запись ![[x] LaTeX formula: [x]](/uploads/formulas/3c345a8aed30f94cb97f496efca2e4209abad676.1.1.png) обозначает наибольшую целую часть некоторого числа, не превосходящую это число, а запись
обозначает наибольшую целую часть некоторого числа, не превосходящую это число, а запись  обозначает его дробную часть. Так, например,
обозначает его дробную часть. Так, например, ![[5]=5 LaTeX formula: [5]=5](/uploads/formulas/fe8313b11ff96c0631a805d611ce610f68ef1323.1.1.png) ,
, ,
, ![[5,2]=5 LaTeX formula: [5,2]=5](/uploads/formulas/b38d2566f98ec709ac7dd5e2d8fdc1a0527d022c.1.1.png) ,
,  ,
, ![[-5,2]=-6 LaTeX formula: [-5,2]=-6](/uploads/formulas/76dbdf9284e376ef10025276768ea473fb6dcc68.1.1.png) ,
,  . Тогда функция
. Тогда функция  является периодической с основным периодом, равным
является периодической с основным периодом, равным  . На рисунке 5.3 построен график этой функции на ее основном периоде
. На рисунке 5.3 построен график этой функции на ее основном периоде  , а на рисунке 5.4 построен график этой функции на нескольких периодах.
, а на рисунке 5.4 построен график этой функции на нескольких периодах.

Точки пересечения графика функции с осью абсцисс называют нулями функции .
Чтобы найти нули функции  необходимо решить уравнение
необходимо решить уравнение  .
.
Функция  обратима
, т. е. имеет обратную функцию
обратима
, т. е. имеет обратную функцию 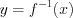 , если она или монотонно возрастает или монотонно убывает на всей своей области определения.
, если она или монотонно возрастает или монотонно убывает на всей своей области определения.
Функции  и
и 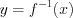 образуют пару взаимно обратных функций. Взаимно обратные функции обладают следующими
свойствами :
образуют пару взаимно обратных функций. Взаимно обратные функции обладают следующими
свойствами :
1) область определения функции  является областью значений функции
является областью значений функции 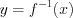 , а область значений функции
, а область значений функции  является областью определения функции
является областью определения функции 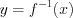 , т.е.
, т.е. 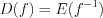 ,
, 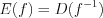 ;
;
2) если функция  монотонно возрастает (убывает), то и функция
монотонно возрастает (убывает), то и функция 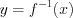 возрастает (убывает);
возрастает (убывает);
3) графики взаимно обратных функций симметричны относительно прямой 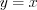 .
.
Чтобы найти функцию обратную функции  необходимо решить уравнение относительно переменной
необходимо решить уравнение относительно переменной  и в этом уравнении заменить
и в этом уравнении заменить  на
на  , а
, а  заменить на
заменить на  .
.
Рассмотрим две функции  и
и  . Функцию вида
. Функцию вида  называют
сложной функцией
.
называют
сложной функцией
.
Например, если ![y=\sqrt[3]{z} LaTeX formula: y=\sqrt[3]{z}](/uploads/formulas/eb9f120857741f922aeb5339ee26436014286970.1.1.png) , а
, а  , то
, то ![f(x)=\sqrt[3]{(x+4)^{5}} LaTeX formula: f(x)=\sqrt[3]{(x+4)^{5}}](/uploads/formulas/465d62d6680ffd2f8ee2297598b9bfa5624d6855.1.1.png) .
.
 .
.  через переменную
через переменную  , получим:
, получим: ,
,  ,
, ![y=\sqrt[3]{0,5-2x} LaTeX formula: y=\sqrt[3]{0,5-2x}](/uploads/formulas/62abe5450dcce86dcff7062b4887ed3cc13a4beb.1.1.png) .
.1) функция
 четная, так как
четная, так как 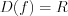 – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и  ;
; 2) функция
 нечетная, так как
нечетная, так как 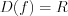 – симметричное множество и
– симметричное множество и ;
; 3) функция
 не является четной и не является нечетной, так как
не является четной и не является нечетной, так как  – не симметричное множество.
– не симметричное множество.Пример 3. Найдите функцию обратную функции
![y=\sqrt[5]{2x+8} LaTeX formula: y=\sqrt[5]{2x+8}](/uploads/formulas/95bdff70178080e93c1c775e0d41223ebccb62ca.1.1.png) .
. Решение . Выразим переменную
 явно:
явно:  ,
,  ,
,  . Заменив в этом уравнении
. Заменив в этом уравнении  на
на  , а
, а  на
на  , запишем:
, запишем:  . Функции
. Функции ![y=\sqrt[5]{2x+8} LaTeX formula: y=\sqrt[5]{2x+8}](/uploads/formulas/95bdff70178080e93c1c775e0d41223ebccb62ca.1.1.png) и
и  взаимно обратные.
взаимно обратные.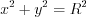 нельзя считать функцией, так как каждому значению
нельзя считать функцией, так как каждому значению  соответствует два значения
соответствует два значения  .
. 
