Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
а) при условии, что
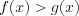 . (7.15.2)
. (7.15.2)






Показательными называют неравенства, содержащие переменную в показателе степени
Методы решений неравенств
1. Если неравенство имеет вид  (
( ,
,  ,
,  ) (7.15), то:
) (7.15), то:
 (
( ,
,  ,
,  ) (7.15), то:
) (7.15), то: а) при условии, что  получим
получим
; (7.15.1)
б) при условии, что  получим
получим
 получим
получим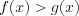 . (7.15.2)
. (7.15.2)2. Если неравенство имеет вид  , то:
, то:
 , то:
, то:а) при  и
и 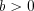 получим
получим  ;
;
 и
и 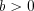 получим
получим  ;
;б) при  и
и  получим
получим  ;
;
 и
и  получим
получим  ;
;в) при  и
и 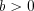 получим
получим  ;
;
 и
и 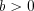 получим
получим  ;
;г) при  и
и  получим
получим  .
.
 и
и  получим
получим  .
. 3. Если неравенство имеет вид  , то:
, то:
 , то:
, то:а) при  и
и 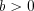 получим
получим  ;
;
 и
и 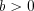 получим
получим  ;
;б) при  и
и  получим
получим  ;
;
 и
и  получим
получим  ;
;в) при  и
и 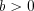 получим
получим  ;
;
 и
и 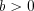 получим
получим  ;
; г) при  и
и  получим
получим  .
.
 и
и  получим
получим  .
.Пример 1. Решите неравенство  .
.
 .
.Поскольку 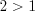 , то получим:
, то получим:  ,
,  ,
,  ,
,  ,
,  .
.
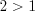 , то получим:
, то получим:  ,
,  ,
,  ,
,  ,
,  .
.Согласно рисунку 7.38 запишем решение неравенства:  .
.
 .
.
Ответ :  .
.
 .
.Пример 2. Решите неравенство  .
.
 .
.Поскольку  , то получим
, то получим  .
.
 , то получим
, то получим  .
.Согласно рисунку 7.39 запишем решение неравенства: ![(0;2] LaTeX formula: (0;2]](/uploads/formulas/b5b889b4dcd233ddd2e55f5c5c7b77d108c229a6.1.1.png) .
.
![(0;2] LaTeX formula: (0;2]](/uploads/formulas/b5b889b4dcd233ddd2e55f5c5c7b77d108c229a6.1.1.png) .
.
Ответ : ![(0;2] LaTeX formula: (0;2]](http://helpy.quali.me/uploads/formulas/b5b889b4dcd233ddd2e55f5c5c7b77d108c229a6.1.1.png) .
.
![(0;2] LaTeX formula: (0;2]](http://helpy.quali.me/uploads/formulas/b5b889b4dcd233ddd2e55f5c5c7b77d108c229a6.1.1.png) .
.Пример 3. Определите число целых решений неравенства  .
.
 .
.Решение. Запишем неравенство в виде  . Разделим обе его части на
. Разделим обе его части на  и получим
и получим  или
или 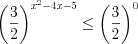 .
.
 . Разделим обе его части на
. Разделим обе его части на  и получим
и получим  или
или 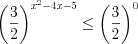 .
. Так как основание степени  , то показательное неравенство равносильно степенному неравенству
, то показательное неравенство равносильно степенному неравенству  .
.
 , то показательное неравенство равносильно степенному неравенству
, то показательное неравенство равносильно степенному неравенству  .
.Решим последнее неравенство методом интервалов (рис. 7.40) и получим ![x\in[-1;5] LaTeX formula: x\in[-1;5]](/uploads/formulas/908163e23cdcc321dae2f73c9ada3cab634ba9fc.1.1.png) .
.
![x\in[-1;5] LaTeX formula: x\in[-1;5]](/uploads/formulas/908163e23cdcc321dae2f73c9ada3cab634ba9fc.1.1.png) .
.
Отрезку ![[-1;5] LaTeX formula: [-1;5]](/uploads/formulas/4dd8f04754c2be17b26c8a1525fc985eda6bfd66.1.1.png) принадлежит 7 целых решений неравенства:
принадлежит 7 целых решений неравенства:  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
![[-1;5] LaTeX formula: [-1;5]](/uploads/formulas/4dd8f04754c2be17b26c8a1525fc985eda6bfd66.1.1.png) принадлежит 7 целых решений неравенства:
принадлежит 7 целых решений неравенства:  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.Ответ:  .
.
 .
.Пример 4. Решите неравенство  .
.
 .
.Решение. Запишем неравенство в виде  и разложим его левую часть на множители.
и разложим его левую часть на множители.
 и разложим его левую часть на множители.
и разложим его левую часть на множители. Получим:  ,
, 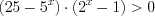 .
.
 ,
, 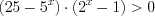 .
. 1. Рассмотрим функцию  .
.
 .
.2. 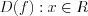 .
.
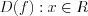 .
.3. Найдем нули функции, решая уравнение  , равносильное совокупности уравнений
, равносильное совокупности уравнений  , откуда
, откуда 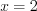 или
или  , откуда
, откуда  .
.
 , равносильное совокупности уравнений
, равносильное совокупности уравнений  , откуда
, откуда 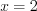 или
или  , откуда
, откуда  .
.4. Нанесем числа 0 и 2 на координатную прямую и определим знаки значений функции на полученных промежутках (рис. 7.41).

5. Решением неравенства является промежуток, на котором функция положительна.
Ответ:  .
.
 .
.Пример 5. Решите неравенство  .
.
 .
.Решение. Запишем данное неравенство в виде  ,
,  и решим его методом интервалов.
и решим его методом интервалов.
 ,
,  и решим его методом интервалов.
и решим его методом интервалов.1. Рассмотрим функцию  .
.
 .
.2.  .
.
 .
.3. Найдем
нули функции, решая уравнение  .
.
 .
.Получим:  , откуда
, откуда  или
или 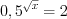 , откуда
, откуда 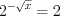 ,
,  и
и  .
.
 , откуда
, откуда  или
или 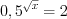 , откуда
, откуда 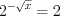 ,
,  и
и  .
.4. Нанесем число  на область определения функции и установим ее знак ее значений на полученном промежутке (рис. 7.42).
на область определения функции и установим ее знак ее значений на полученном промежутке (рис. 7.42).
 на область определения функции и установим ее знак ее значений на полученном промежутке (рис. 7.42).
на область определения функции и установим ее знак ее значений на полученном промежутке (рис. 7.42).
Ответ :  .
.
 .
.Покажем решение показательно-степенного неравенства  (
(  ;
;  ;
;  ). (7.16)
). (7.16)
 (
(  ;
;  ;
;  ). (7.16)
). (7.16)Запишем это неравенство в виде 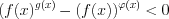 и рассмотрим функцию
и рассмотрим функцию  .
.
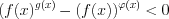 и рассмотрим функцию
и рассмотрим функцию  .
. Находя нули функции 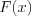 , решим уравнения:
, решим уравнения:
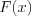 , решим уравнения:
, решим уравнения: 1)  , при условии, что
, при условии, что 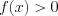 и
и  (случай
(случай 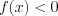 нами не рассматривается);
нами не рассматривается);
 , при условии, что
, при условии, что 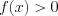 и
и  (случай
(случай 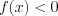 нами не рассматривается);
нами не рассматривается); 2) 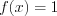 ;
;
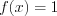 ;
;3)  .
.
 .
. Обратим внимание на то, что необходима проверка корней уравнения  , так как, подставив полученные числа в уравнение
, так как, подставив полученные числа в уравнение 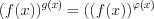 , можем получить неопределенность вида
, можем получить неопределенность вида 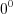 или
или  . Такие числа исключают из множества решений данного неравенства.
. Такие числа исключают из множества решений данного неравенства.
 , так как, подставив полученные числа в уравнение
, так как, подставив полученные числа в уравнение 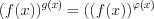 , можем получить неопределенность вида
, можем получить неопределенность вида 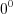 или
или  . Такие числа исключают из множества решений данного неравенства.
. Такие числа исключают из множества решений данного неравенства. Пример. Решите неравенство 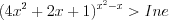 .
.
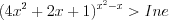 .
.1. Рассмотрим функцию  .
.
 .
.2. 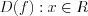 .
.
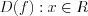 .
.3. Найдем нули функции, решая уравнение  :
:
 :
:а)  ,
, 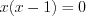 , откуда
, откуда  ,
,  ;
;
 ,
, 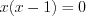 , откуда
, откуда  ,
,  ;
;б)  ,
,  , откуда
, откуда 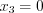 ,
,  ;
;
 ,
,  , откуда
, откуда 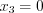 ,
,  ;
;в)  , откуда
, откуда  .
.
 , откуда
, откуда  .
.4. Нанесем нули функции на координатную прямую и определим знаки значений функции на полученных промежутках (рис. 7.43).

5. Решением неравенства являются промежутки, на которых функция положительна.
Ответ :  .
.
 .
.


