Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
Уравнения с одной переменной
Равенство, содержащее переменную, называют уравнением и записывают 

Областью определения (или областью допустимых значений) уравнения  называют общую часть областей определения функций
называют общую часть областей определения функций  и
и 
 называют общую часть областей определения функций
называют общую часть областей определения функций  и
и 
Значение переменной, при подстановке которого в уравнение получаем верное равенство, называют корнем (решением) уравнения.
Решить уравнение – значит найти все его корни или доказать, что их нет.
Число  называют корнем кратности
называют корнем кратности  многочлена
многочлена  если справедливо равенство
если справедливо равенство  где
где  – многочлен степени
– многочлен степени  и
и  – натуральные числа
– натуральные числа  и
и 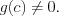
 называют корнем кратности
называют корнем кратности  многочлена
многочлена  если справедливо равенство
если справедливо равенство  где
где  – многочлен степени
– многочлен степени  и
и  – натуральные числа
– натуральные числа  и
и 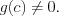
Равносильные и неравносильные уравнения
Уравнения  и
и  называют равносильными, если множества их решений совпадают (они имеют равные корни либо не имеют корней). Записывают:
называют равносильными, если множества их решений совпадают (они имеют равные корни либо не имеют корней). Записывают: 
 и
и  называют равносильными, если множества их решений совпадают (они имеют равные корни либо не имеют корней). Записывают:
называют равносильными, если множества их решений совпадают (они имеют равные корни либо не имеют корней). Записывают: 
Например: 1) уравнения  и
и  равносильны, так решением каждого из этих уравнений является только число
равносильны, так решением каждого из этих уравнений является только число  2) уравнения
2) уравнения  и
и  равносильны, так как каждое из этих уравнений не имеет решений.
равносильны, так как каждое из этих уравнений не имеет решений.
 и
и  равносильны, так решением каждого из этих уравнений является только число
равносильны, так решением каждого из этих уравнений является только число  2) уравнения
2) уравнения  и
и  равносильны, так как каждое из этих уравнений не имеет решений.
равносильны, так как каждое из этих уравнений не имеет решений.Уравнение  является следствием уравнения
является следствием уравнения  если его решение содержит все корни уравнения
если его решение содержит все корни уравнения  Записывают:
Записывают: 
 является следствием уравнения
является следствием уравнения  если его решение содержит все корни уравнения
если его решение содержит все корни уравнения  Записывают:
Записывают: 
Например, уравнение  является следствием уравнения
является следствием уравнения  так как корнем уравнения
так как корнем уравнения  является число
является число  а корнями уравнения
а корнями уравнения  – числа
– числа 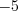 и
и 
 является следствием уравнения
является следствием уравнения  так как корнем уравнения
так как корнем уравнения  является число
является число  а корнями уравнения
а корнями уравнения  – числа
– числа 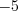 и
и 
Если выполняются условия  и
и  то
то 
 и
и  то
то 
Равносильные уравнения получают в результате следующих преобразований:
1. При переносе слагаемых из одной части уравнения в другую с противоположным знаком.
2. При умножении или делении обеих частей уравнения на одно и то же отличное от нуля число.
3. При замене уравнения 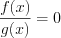 системой уравнений
системой уравнений 
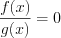 системой уравнений
системой уравнений 
Существует ряд преобразований уравнений, которые могут привести к уравнению, неравносильному данному:
1. Возведение обеих частей уравнения в четную степень (в результате могут появиться посторонние корни).
Например,уравнения  и
и  не равносильны, так как уравнение
не равносильны, так как уравнение  корней не имеет, а уравнение
корней не имеет, а уравнение  имеет корень
имеет корень 
 и
и  не равносильны, так как уравнение
не равносильны, так как уравнение  корней не имеет, а уравнение
корней не имеет, а уравнение  имеет корень
имеет корень 
2. Умножение обеих частей уравнения на выражение, содержащее переменную (могут появиться посторонние корни).
Например, уравнения  и
и  не равносильны, так как корнем уравнения
не равносильны, так как корнем уравнения  является только число
является только число  а корнями уравнения
а корнями уравнения  являются числа
являются числа  и
и 
 и
и  не равносильны, так как корнем уравнения
не равносильны, так как корнем уравнения  является только число
является только число  а корнями уравнения
а корнями уравнения  являются числа
являются числа  и
и 
3. Деление обеих частей уравнения на выражение, содержащее переменную (может произойти потеря корней).
Например, 1) уравнения  и
и  не равносильны, так как корнями уравнения
не равносильны, так как корнями уравнения  являются числа
являются числа  и
и  а корнем уравнения
а корнем уравнения  является только число
является только число 
 и
и  не равносильны, так как корнями уравнения
не равносильны, так как корнями уравнения  являются числа
являются числа  и
и  а корнем уравнения
а корнем уравнения  является только число
является только число 
Пример 1. Найдите область определения уравнения ![\frac{x-5}{21x}=\sqrt[3]{6+x}. LaTeX formula: \frac{x-5}{21x}=\sqrt[3]{6+x}.](/uploads/formulas/7bba61303c94aa13d9a3b3e43e6c78c6c5ef8a5d.1.1.png)
![\frac{x-5}{21x}=\sqrt[3]{6+x}. LaTeX formula: \frac{x-5}{21x}=\sqrt[3]{6+x}.](/uploads/formulas/7bba61303c94aa13d9a3b3e43e6c78c6c5ef8a5d.1.1.png)
Решение. Так как функция  определена на множестве всех действительных чисел, за исключением числа нуль, а функция
определена на множестве всех действительных чисел, за исключением числа нуль, а функция ![g(x)=\sqrt[3]{6+x}. LaTeX formula: g(x)=\sqrt[3]{6+x}.](/uploads/formulas/63e15ff02c3736b98a64dbece0d278c396c410a8.1.1.png) определена на множестве всех действительных чисел, то область определения данного уравнения имеет вид:
определена на множестве всех действительных чисел, то область определения данного уравнения имеет вид: 
 определена на множестве всех действительных чисел, за исключением числа нуль, а функция
определена на множестве всех действительных чисел, за исключением числа нуль, а функция ![g(x)=\sqrt[3]{6+x}. LaTeX formula: g(x)=\sqrt[3]{6+x}.](/uploads/formulas/63e15ff02c3736b98a64dbece0d278c396c410a8.1.1.png) определена на множестве всех действительных чисел, то область определения данного уравнения имеет вид:
определена на множестве всех действительных чисел, то область определения данного уравнения имеет вид: 
Уравнения с двумя переменными
Решением уравнения  с двумя переменными
с двумя переменными  и
и  является упорядоченная пара
является упорядоченная пара 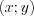 чисел, при подстановке которых в уравнение, получим верное числовое равенство.
чисел, при подстановке которых в уравнение, получим верное числовое равенство.
 с двумя переменными
с двумя переменными  и
и  является упорядоченная пара
является упорядоченная пара 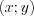 чисел, при подстановке которых в уравнение, получим верное числовое равенство.
чисел, при подстановке которых в уравнение, получим верное числовое равенство.Например: решение уравнения  образует множество пар чисел таких как
образует множество пар чисел таких как  и т. д.
и т. д.
 образует множество пар чисел таких как
образует множество пар чисел таких как  и т. д.
и т. д.Систему двух уравнений  и
и  с двумя переменными
с двумя переменными  и
и  записывают в виде
записывают в виде 
 и
и  с двумя переменными
с двумя переменными  и
и  записывают в виде
записывают в виде 
Решение системы уравнений образуют только те пары чисел, которые являются решениями каждого уравнения системы.

