Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
Опытом (испытанием, экспериментом) называют осуществление комплекса условий или действий, при которых наблюдается соответствующее явление.
Событие – возможный результат опыта.
Если событие не разбивается на более простые составляющие, то его называют элементарным.
Для обозначения событий используют любую заглавную букву или набор букв, например: ,
,  ,
,  ,
, 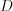 и т.п.
и т.п.
Н а п р и м е р, в результате игры в шахматы могут произойти следующие события: «выигрыш», «проигрыш», «ничья».
Если событие не разбивается на более простые составляющие, то его называют элементарным.
Для обозначения событий используют любую заглавную букву или набор букв, например:
 ,
,  ,
,  ,
, 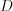 и т.п.
и т.п. Н а п р и м е р, в результате игры в шахматы могут произойти следующие события: «выигрыш», «проигрыш», «ничья».
События равновозможные, если нет оснований полагать, что у одного события есть больше шансов появиться, чем у другого.
Н а п р и м е р, при подбрасывании монеты события (появление на верхней стороне монеты орла) и
(появление на верхней стороне монеты орла) и  (появление решка) будут равновозможными, если монета не деформирована.
(появление решка) будут равновозможными, если монета не деформирована.
Н а п р и м е р, при подбрасывании монеты события
 (появление на верхней стороне монеты орла) и
(появление на верхней стороне монеты орла) и  (появление решка) будут равновозможными, если монета не деформирована.
(появление решка) будут равновозможными, если монета не деформирована.Классификация событий
1. Достоверные события, которые обязательно произойдут в данном опыте.
Н а п р и м е р, из урны, в которой находятся красные и синие шары, наудачу извлекается один шар. Событие «появление не белого шара» – достоверное.
Н а п р и м е р, из урны, в которой находятся красные и синие шары, наудачу извлекается один шар. Событие «появление не белого шара» – достоверное.
2. Случайные события, которые могут произойти, а могут и не произойти в данном опыте.
Н а п р и м е р, из урны, в которой находятся красные и синие шары, наудачу извлекается один шар. Событие «появление синего шара» – случайное, событие «появление не красного шара» – случайное.
Н а п р и м е р, из урны, в которой находятся красные и синие шары, наудачу извлекается один шар. Событие «появление синего шара» – случайное, событие «появление не красного шара» – случайное.
3. Невозможные события, которые никогда не произойдут в данном опыте.
Н а п р и м е р, из урны, в которой находятся красные и синие шары, наудачу извлекается один шар. Событие «появление черного шара» – невозможное.
Н а п р и м е р, из урны, в которой находятся красные и синие шары, наудачу извлекается один шар. Событие «появление черного шара» – невозможное.
Достоверные события, как правило, обозначают буквой  , а невозможные буквой
, а невозможные буквой  .
.
 , а невозможные буквой
, а невозможные буквой  .
. Два события называют совместными в данном опыте, если появление одного из них не исключает появления и другого.
Н а п р и м е р, если подбросить две монеты, то события «появилась решка» и событие
«появилась решка» и событие  «появился орел» будут совместными. Если подбросить одну монету, то события
«появился орел» будут совместными. Если подбросить одну монету, то события  и
и  будут несовместными.
будут несовместными.
Н а п р и м е р, если подбросить две монеты, то события
 «появилась решка» и событие
«появилась решка» и событие  «появился орел» будут совместными. Если подбросить одну монету, то события
«появился орел» будут совместными. Если подбросить одну монету, то события  и
и  будут несовместными.
будут несовместными.Два события называют противоположными в данном опыте, если появление одного из них равносильно не появлению другого. Обозначают:  и
и 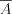 .
.
Н а п р и м е р, «выигрыш» и «проигрыш» лотерейного билета.
 и
и 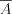 .
. Н а п р и м е р, «выигрыш» и «проигрыш» лотерейного билета.
Множество событий называют полной группой событий, если они попарно несовместны и появление одного и только одного из них является достоверным событием.
Н а п р и м е р, если бросить игральный кубик, то может быть шесть исходов (событий) и они образуют полную группу событий:
 (на верхней грани выпала цифра 1),
(на верхней грани выпала цифра 1),  (цифра 2),
(цифра 2),  ,
,  ,
,  ,
,  .
.
Н а п р и м е р, если бросить игральный кубик, то может быть шесть исходов (событий) и они образуют полную группу событий:
 (на верхней грани выпала цифра 1),
(на верхней грани выпала цифра 1),  (цифра 2),
(цифра 2),  ,
,  ,
,  ,
,  .
.Вероятностью события называют числовую характеристику, определяющую степень возможности интересующего результата в условиях проводимого опыта.
Вероятность события обозначают
обозначают  .
.
Вероятность события
 обозначают
обозначают  .
.Определения вероятности события
1. Классическое:
 , (10.1)
, (10.1)
где – количество всевозможных исходов опыта, которые образуют полную группу событий,
– количество всевозможных исходов опыта, которые образуют полную группу событий,  – количество исходов, благоприятствующих появлению события
– количество исходов, благоприятствующих появлению события  .
.
Н а п р и м е р, если подбросить монету, то вероятности событий «появилась решка» и
«появилась решка» и  «появился орел», будут равны:
«появился орел», будут равны:  ,
,  .
.
 , (10.1)
, (10.1) где
 – количество всевозможных исходов опыта, которые образуют полную группу событий,
– количество всевозможных исходов опыта, которые образуют полную группу событий,  – количество исходов, благоприятствующих появлению события
– количество исходов, благоприятствующих появлению события  .
. Н а п р и м е р, если подбросить монету, то вероятности событий
 «появилась решка» и
«появилась решка» и  «появился орел», будут равны:
«появился орел», будут равны:  ,
,  .
.2. Статистическое (относительная частота события):
 , (10.2)
, (10.2)
где – количество проведенных опытов,
– количество проведенных опытов,  – количество опытов, в которых появилось событие
– количество опытов, в которых появилось событие  .
.
 , (10.2)
, (10.2) где
 – количество проведенных опытов,
– количество проведенных опытов,  – количество опытов, в которых появилось событие
– количество опытов, в которых появилось событие  .
.Свойства вероятностей
1. Вероятность достоверного события равна  , так как
, так как  .
.
 , так как
, так как  .
.2. Вероятность невозможного события рана  , так как
, так как  .
.
 , так как
, так как  .
.3. Вероятность случайного события  , так как
, так как  .
.
 , так как
, так как  .
. Следовательно, вероятность любого события удовлетворяет неравенствам:
 . (10.3)
. (10.3)
 . (10.3)
. (10.3)Пример 1. Из урны, в которой находится  красных,
красных,  синих и
синих и  оранжевых шара, наудачу извлекается один шар. Какова вероятность того, что извлечен:
оранжевых шара, наудачу извлекается один шар. Какова вероятность того, что извлечен:
1) красный шар; 2) не оранжевый шар; 3) не зеленый шар; 4) белый шар?
Решение. Вероятность события находят по формуле 10.1 .
Количество всевозможных исходов: .
.
1. Вероятность того, что будет извлечен красный шар (благоприятных исходов ), равна:
), равна:
 .
.
2. Вероятность того, что будет извлечен не оранжевый шар (красный или синий), равна:
 .
.
3. Вероятность того, что будет извлечен не зеленый шар (все шары не зеленые), равна:
 .
.
4. Вероятность того, что будет извлечен белый шар (таких шаров нет), равна:
 .
.
 красных,
красных,  синих и
синих и  оранжевых шара, наудачу извлекается один шар. Какова вероятность того, что извлечен:
оранжевых шара, наудачу извлекается один шар. Какова вероятность того, что извлечен: 1) красный шар; 2) не оранжевый шар; 3) не зеленый шар; 4) белый шар?
Решение. Вероятность события находят по формуле 10.1 .
Количество всевозможных исходов:
 .
. 1. Вероятность того, что будет извлечен красный шар (благоприятных исходов
 ), равна:
), равна:  .
. 2. Вероятность того, что будет извлечен не оранжевый шар (красный или синий), равна:
 .
.3. Вероятность того, что будет извлечен не зеленый шар (все шары не зеленые), равна:
 .
.4. Вероятность того, что будет извлечен белый шар (таких шаров нет), равна:
 .
.Пример 2. Монету подбросили 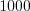 раз. Оказалось, что цифра появилась
раз. Оказалось, что цифра появилась  раза. Найдите относительную частоту этого события.
раза. Найдите относительную частоту этого события.
Решение. Относительную частоту события находят по формуле 10.2 .
Поскольку количество проведенных опытов , а количество опытов, в которых появилась цифра (событие
, а количество опытов, в которых появилась цифра (событие  )
)  , то относительная частота этого события равна:
, то относительная частота этого события равна:
 .
.
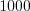 раз. Оказалось, что цифра появилась
раз. Оказалось, что цифра появилась  раза. Найдите относительную частоту этого события.
раза. Найдите относительную частоту этого события. Решение. Относительную частоту события находят по формуле 10.2 .
Поскольку количество проведенных опытов
 , а количество опытов, в которых появилась цифра (событие
, а количество опытов, в которых появилась цифра (событие  )
)  , то относительная частота этого события равна:
, то относительная частота этого события равна:  .
.Ответ:  .
.
 .
.1. Закономерности появления массовых случайных событий изучает наука теория вероятностей.
2. При достаточно большом количестве опытов относительная частота события приближается к теоретической вероятности этого события.
3. Если события  ,
,  , …,
, …,  образуют полную группу событий, то
образуют полную группу событий, то  .
.
 ,
,  , …,
, …,  образуют полную группу событий, то
образуют полную группу событий, то  .
.4. Сумма вероятностей противоположных событий равна  .
.
Так, если , а
, а  , то
, то 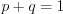 .
.
 .
. Так, если
 , а
, а  , то
, то 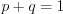 .
.
