 , (9.7)
, (9.7) где
 – действительные числа, которые называют
коэффициентами ряда.
– действительные числа, которые называют
коэффициентами ряда. При  степенной ряд принимает вид:
степенной ряд принимает вид:  (9.8)
(9.8)
Теорема Абеля : если степенной ряд 9.8 сходится в точке  , то он сходится абсолютно в любой точке
, то он сходится абсолютно в любой точке  , такой, что
, такой, что  .
.
Следствие: если степенной ряд
9.8
расходится в точке  , то он расходится в любой точке
, то он расходится в любой точке  , такой, что
, такой, что  .
.
Для степенного ряда
9.8
радиусом сходимости называют такое число  , что при
, что при  ряд сходится, а при
ряд сходится, а при расходится.
расходится.
Интервал  называют интервалом сходимости
ряда.
называют интервалом сходимости
ряда.
Для степенного ряда 9.7 число  называют радиусом сходимости
, если при
называют радиусом сходимости
, если при  ряд сходится, а при
ряд сходится, а при расходится.
расходится.
Интервал  называют
интервалом сходимости этого ряда.
называют
интервалом сходимости этого ряда.
Радиус сходимости
находят по одной из формул:
 ; (9.9)
; (9.9)
![R=\left (\lim_{n \to \infty } \sqrt[n]{c_{n}}\right )^{-1} LaTeX formula: R=\left (\lim_{n \to \infty } \sqrt[n]{c_{n}}\right )^{-1}](/uploads/formulas/9ab2bfddfc23c8fe17f58dc8fd8509a9d08e2f61.1.1.png) . (9.10)
. (9.10)
Интервал сходимости
находят, используя признак Даламбера или Коши:
 ; (9.11)
; (9.11)
![\lim_{n \to \infty }\left |\sqrt[n]{u_{n}}\right |< 1 LaTeX formula: \lim_{n \to \infty }\left |\sqrt[n]{u_{n}}\right |< 1](/uploads/formulas/8d6eab2c421b544abb33b41cdacaa1f615a85609.1.1.png) . (9.12)
. (9.12)
Ряд Тейлора и ряд Маклорена
Если функция  разлагается в степенной ряд
разлагается в степенной ряд
 (
( )
)в некоторой окрестности точки  , то ее можно представить в виде:
, то ее можно представить в виде:

 (9.13)
(9.13)
Ряд, записанный в правой части формулы 9.13, называют рядом Тейлора
для функции  и в окрестности точки
и в окрестности точки  .
.
Если функция  бесконечно дифференцируема в окрестности точки
бесконечно дифференцируема в окрестности точки  , то есть в интервале
, то есть в интервале  , и ее производные равномерно ограничены в этом интервале, то ее всегда можно разложить в ряд Тейлора.
, и ее производные равномерно ограничены в этом интервале, то ее всегда можно разложить в ряд Тейлора.
При  получим
ряд Маклорена
для функции
получим
ряд Маклорена
для функции  :
:
 . (9.14)
. (9.14)
Разложения некоторых функций в ряд Маклорена 9.14:
 ;
; ;
;  ;
; .
. .
.Решение. Найдем радиус сходимости ряда.
Запишем
 ,
,  и применим формулу 9.9:
и применим формулу 9.9: 
 .
. , а
, а  , то интервал сходимости этого ряда можем найти так:
, то интервал сходимости этого ряда можем найти так: ,
,  ,
,  .
. Ответ :
 ;
;  .
. Пример 2.
Найдите область сходимости ряда .
.
 ,
,  .
. Применим признак Даламбера 9.11:


 .
. , откуда
, откуда  ,
,  – интервал сходимости ряда.
– интервал сходимости ряда.На концах промежутка
![\left [ -1;1 \right ] LaTeX formula: \left [ -1;1 \right ]](/uploads/formulas/12687c7ff829e15272b0c793fefa3484ca1b7bb2.1.1.png) ряд может сходиться или расходиться.
ряд может сходиться или расходиться. При
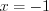 получим знакочередующийся ряд
получим знакочередующийся ряд  .
. Применим признак Лейбница:
1)
 ,
,  и
и 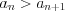 ;
; 2)
 .
. Следовательно, ряд сходится.
При
 получим ряд Дрихле
получим ряд Дрихле  , который сходится.
, который сходится.Ответ :
![\left [ -1;1 \right ] LaTeX formula: \left [ -1;1 \right ]](/uploads/formulas/12687c7ff829e15272b0c793fefa3484ca1b7bb2.1.1.png) .
.
Пример 3.
Разложите в ряд Маклорена 9.14 функцию  .
.
Решение. Найдем значение функции в точке  :
:
 .
.
Найдем производные данной функции и значения производных в точке  :
:  ,
,  ;
;  ,
,  ;
;  ,
,  ;
;
…  ,
,
 .
.
Согласно формуле 9.14 запишем:




![\left [ -R;R \right ] LaTeX formula: \left [ -R;R \right ]](/uploads/formulas/df7c81f0a22f84522c37e7c8db6485b7156a6fa9.1.1.png) степенной
ряд может или сходиться или расходиться.
степенной
ряд может или сходиться или расходиться. , то ряд
, то ряд
 , то ряды
, то ряды
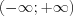 .
.