Числовые ряды с положительными членами /qualihelpy

Числовые ряды с положительными членами

Справочник / Студент / Ряды /

Справочный материал Примеры Обратите внимание! Видео Модели Пройти тесты

Рассмотрим ряд $LaTeX formula: \sum_{n=1}^{\infty }a_{n}$ с положительными членами.

Признаки сходимости

1. Признак Даламбера.
Если существует предел $LaTeX formula: \lim_{n \to \infty }\frac{a_{n+1}}{a_{n}}=l$ и LaTeX formula: l< 1 , то ряд сходится, а если LaTeX formula: l> 1 , то ряд расходится.
Если LaTeX formula: l=1 , то необходимо воспользоваться другим признаком.

2. Радикальный признак Коши.
Если существует предел $LaTeX formula: \lim_{n \to \infty }\sqrt[n]{a_{n}}=l$ и LaTeX formula: l< 1 , то ряд сходится, а если LaTeX formula: l> 1 , то ряд расходится.
Если LaTeX formula: l=1 , то необходимо воспользоваться другим признаком.

3. Интегральный признак Коши.
Если члены ряда положительны и не возрастают и несобственный интеграл $LaTeX formula: \int_{1}^{\infty }a_{n}dn$ сходится, то и ряд сходится, а если интеграл расходится (равен бесконечности или не существует), то и ряд расходится.

4. Признаки сравнения рядов $LaTeX formula: \sum_{n=1}^{\infty }a_{n}$ (1) и $LaTeX formula: \sum_{n=1}^{\infty }b_{n}$ (2).
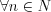
1. Если $LaTeX formula: \forall n\in N$ $LaTeX formula: a_{n}\leq b_{n}$ и ряд (2) сходится, то и ряд (1) сходится, а если ряд (1) расходится, то и ряд (2) расходится.
2. Если существует предел $LaTeX formula: \lim_{n \to \infty }\frac{a_{n}}{b_{n}}=c\neq 0$ , то ряды ( 1 ) и ( 2 ) сходятся или расходятся одновременно.

Пример 1. Исследуйте на сходимость ряд $LaTeX formula: \sum_{n=1}^{\infty }\frac{2^{n}}{(2n)!}$ .
Решение. Применим признак Даламбера.

Так как $LaTeX formula: a_{n}=\frac{2^{n}}{(2n)!}$ , а $LaTeX formula: a_{n+1}=\frac{2^{n+1}}{(2n+2)!}$ , то

$LaTeX formula: \frac{a_{n+1}}{a_{n}}=\frac{2^{n+1}}{(2n+2)!}\cdot \frac{(2n)!}{2^{n}}=$ $LaTeX formula: \frac{2^{n}\cdot 2\cdot (2n)!}{(2n)!(2n+1)(2n+2)2^{n}}=\frac{2}{4n^{2}+5n+2}$ .

Тогда $LaTeX formula: \lim_{n \to \infty }\frac{a_{n+1}}{a_{n}}=2\lim_{n \to \infty }\frac{1}{n^{2}+5n+2}=2\cdot 0=0< 1$ .
Ответ: Ряд сходится.

Пример 2. Исследуйте на сходимость ряд $LaTeX formula: \sum_{n=1}^{\infty }\left (\frac{2n-3}{5n+2} \right )^{n}$ .
Решение. Применим радикальный признак Коши.
Так как $LaTeX formula: \lim_{n\rightarrow \infty }\sqrt[n]{\left ( \frac{2n-3}{5n+2} \right )^{n}}=\lim_{n \to \infty }\frac{2n-3}{5n+2}=\frac{2-0}{5+0}=0,4< 1$ , то ряд сходится.

Ответ: Ряд сходится.

Пример 3. Исследуем на сходимость ряд Дирихле $LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{n^{p}}$ .
Решение. Так как члены ряда положительны и не возрастают, то применим интегральный признак Коши.
Составим интеграл $LaTeX formula: \int_{1}^{\infty }\frac{dn}{n^{p}}$ и рассмотрим три случая:
1) при LaTeX formula: p=1 получим $LaTeX formula: \int_{1}^{\infty }\frac{dn}{n}=\ln n|_{1}^{\infty }=\lim_{n \to \infty }\ln n-\ln 1=\infty -1=\infty$ ,
следовательно, ряд расходится;
2) при LaTeX formula: p> 1 получим
$LaTeX formula: I=\int_{1}^{\infty }n^{-p}dn=\frac{n^{-p+1}}{-p+1}\left.\begin{matrix} & \\ & \end{matrix}\right|_{1}^{\infty }=\frac{1}{1-p}n^{-p+1}\left.\begin{matrix} & \\ & \end{matrix}\right|_{1}^{\infty }$ ,

$LaTeX formula: I=\frac{1}{1-p}\left ( \left ( \lim_{n \to \infty } \frac{1}{n}\right ) ^{p-1}-1\right )=\frac{1}{1-p}(0-1)=\frac{1}{p-1}$ .

следовательно, ряд сходится;
3) при LaTeX formula: p< 1 получим $LaTeX formula: \int_{1}^{\infty }n^{-p}dn=\frac{1}{1-p}\left ( \left ( \lim_{n \to \infty } n\right )^{1-p} -1\right )=\frac{1}{1-p}(\infty -1)=\infty$ ,
следовательно, ряд расходится.

1. Гармонический ряд $LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{n}$ расходится.
Ряд Дирихле $LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{n^{p}}$ сходится при LaTeX formula: p> 1

и расходится при $LaTeX formula: p\leq 1$ .
2. Факториалом натурального числа LaTeX formula: n

называют произведение натуральных чисел от LaTeX formula: 1

до

включительно: $LaTeX formula: n!=1\cdot 2\cdot 3\cdot ...\cdot (n-1)\cdot n$ .
Н а п р и м е р: $LaTeX formula: 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120$ ; $LaTeX formula: 5!=4!\cdot 5=120$ ; $LaTeX formula: \frac{100!}{98!}=\frac{98!\cdot 99\cdot 100}{98!}=9900$ .

Программа для просмотра моделей (МК-плеер) Файлы для скачивания

Числовые ряды с положительными числами