Понятие числового ряда /qualihelpy

Понятие числового ряда

Справочник / Студент / Ряды /

Справочный материал Примеры Обратите внимание! Видео Модели Пройти тесты

Числовым рядом называют выражение вида:
$LaTeX formula: \sum_{n=1}^{\infty }a_{n}=a_{1}+a_{2}+a_{3}+...+a_{n}+...$ , (9.1)
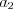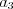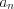где $LaTeX formula: a_{1}$ , $LaTeX formula: a_{2}$ , $LaTeX formula: a_{3}$ , …, $LaTeX formula: a_{n}$ , … – последовательность чисел, которые называют членами ряда .

Ряд 9.1 задан, если известно правило, по которому находится его общий член:
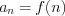$LaTeX formula: a_{n}=f(n)$ , где $LaTeX formula: n\in N$ .

Примеры числовых рядов

1. Арифметический ряд.
Рассмотрим арифметическую прогрессию, общий член которой задается формулой:
$LaTeX formula: a_{n}=a_{1}+d(n-1)$ .
Н а п р и м е р, пусть $LaTeX formula: a_{1}=1$ , а LaTeX formula: d=2 . Тогда $LaTeX formula: a_{n}=1+2(n-1)=2n-1$ .
Запишем арифметический ряд:
$LaTeX formula: \sum_{n=1}^{\infty }(2n-1)=1+3+5+7+9+...$

2. Геометрический ряд.
Рассмотрим геометрическую прогрессию, общий член которой задается формулой:
$LaTeX formula: b_{n}=b_{1}q^{n-1}$ .
Н а п р и м е р, пусть $LaTeX formula: b_{1}=1$ , а LaTeX formula: q=2 . Тогда $LaTeX formula: b_{n}=2^{n-1}$ .
Запишем геометрический ряд:
$LaTeX formula: \sum_{n=1}^{\infty }2^{n-1}=1+2+4+8+16+...$
Н а п р и м е р, если $LaTeX formula: b_{1}=1$ и $LaTeX formula: q=\frac{1}{2}$ , то получим ряд:
$LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{2^{n-1}}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...$

3. Гармонический ряд.
Гармоническим рядом называют ряд вида:
$LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{n}+...$ (9.2)

4. Ряд Дирихле.
Рядом Дирихле называют ряд вида:
$LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{n^{p}}=1+\frac{1}{2^{p}}+\frac{1}{3^{p}}+\frac{1}{4^{p}}+...+\frac{1}{n^{p}}+...$ , (9.3)
где $LaTeX formula: p\in R$ . При LaTeX formula: p=1 получаем гармонический ряд.

Сумма числового ряда

1. Частичной n-й суммой ряда называют сумму конечного числа его LaTeX formula: n первых членов:
$LaTeX formula: S_{n}=a_{1}+a_{2}+a_{3}+...+a_{n}$ . (9.4)

Н а п р и м е р:
1) частичную сумму арифметического ряда находят по формуле:
$LaTeX formula: S_{n}=\frac{2a_{1}n+dn(n-1)}{2}$ ;
2) частичную сумму геометрического ряда находят по формуле:
$LaTeX formula: S_{n}=\frac{b_{1}(1-q^{n})}{1-q}$ .

2. Суммой S ряда называют предел его частичной суммы $LaTeX formula: S_{n}$ при LaTeX formula: n стремящемся к бесконечности:
$LaTeX formula: S=\lim_{n \mapsto\infty }S_{n}$ . (9.5)

Сходимость числовых рядов

Ряд 9.1 сходится , если существует предел последовательности его частичных сумм.

Ряд 9.1 расходится , если предел последовательности его частичных сумм не существует или равен бесконечности.

Необходимое условие сходимости числового ряда 9.1 :
если ряд сходится, то $LaTeX formula: \lim_{n \mapsto\infty }a_{n}=0$ .

Следствие из необходимого признака сходимости:
если $LaTeX formula: \lim_{n \mapsto\infty }a_{n}\neq 0$ , то ряд 9.1 расходится.

Н а п р и м е р: ряд $LaTeX formula: \sum_{n=1}^{\infty }\frac{2n+1}{n+1}$ расходится, так как $LaTeX formula: \lim_{n \to \infty }\frac{2n+1}{n+1}=2\neq 0$ .

Пример. Исследуем на сходимость арифметический и геометрический ряды.
Решение.
1. Арифметический ряд расходится.
Действительно: $LaTeX formula: \lim_{n \to \infty }S_{n}=\lim_{n \to \infty }\frac{2a_{1}n+dn(n-1)}{2}=\infty$ .

2. Геометрический ряд при $LaTeX formula: \left | q \right |< 1$ сходится.
Действительно:
$LaTeX formula: \lim_{n \to \infty }S_{n}=\lim_{n \to \infty }\frac{b_{1}(1-q^{n})}{1-q}=\frac{b_{1}}{1-q}\lim_{n \to \infty }(1-q^{n})$ $LaTeX formula: =\frac{b_{1}}{1-q}(1-0)=\frac{b_{1}}{1-q}$ .

3. Геометрический ряд при $LaTeX formula: \left | q \right |> 1$ расходится.
Действительно:
$LaTeX formula: \lim_{n \to \infty }S_{n}=\lim_{n \to \infty }\frac{b_{1}(1-q^{n})}{1-q}=\frac{b}{1-q}\lim_{n \to \infty }(q^{n}-1)=\frac{b_{1}}{1-q}(\infty -1)$ $LaTeX formula: =\infty$ .

Если $LaTeX formula: \lim_{n \to \infty }a_{n}=0$ , то ряд $LaTeX formula: \sum_{n=1}^{\infty }a_{n}$ может сходиться, а может расходиться.
Н а п р и м е р:
1) геометрический ряд сходится $LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{2^{n-1}}$ , а $LaTeX formula: \lim_{n \to \infty }\frac{1}{2^{n-1}}=0$ ;
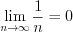2) гармонический ряд 9.2 расходится, а $LaTeX formula: \lim_{n \to \infty }\frac{1}{n}=0$ .

Программа для просмотра моделей (МК-плеер) Файлы для скачивания