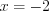Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (8.6)
. (8.6)  . (8.7)
. (8.7)  , (8.8)
, (8.8)
где и
и  однородные функции одного и того же порядка:
однородные функции одного и того же порядка:  и
и  .
.  . (8.10)
. (8.10)
 ,
,  ,
,  .
.  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Учитывая, что , получим:
, получим:
 ,
, 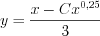 .
.
Ответ: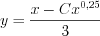 .
.
Дифференциальным уравнением  -го порядка называют уравнение вида:
-го порядка называют уравнение вида:
 , (8.1)
, (8.1)
где – неизвестная функция, а
– неизвестная функция, а  , , …, – ее производные.
, , …, – ее производные.
 -го порядка называют уравнение вида:
-го порядка называют уравнение вида:  , (8.1)
, (8.1) где
 – неизвестная функция, а
– неизвестная функция, а  , , …, – ее производные.
, , …, – ее производные.Дифференциальным уравнением первого порядка называют уравнение вида:
 . (8.2)
. (8.2)
 . (8.2)
. (8.2) Н а п р и м е р,  ,
,  ,
,  ,
,  ,
,  ,
,  – дифференциальные уравнения первого порядка.
– дифференциальные уравнения первого порядка.
 ,
,  ,
,  ,
,  ,
,  ,
,  – дифференциальные уравнения первого порядка.
– дифференциальные уравнения первого порядка.Общим решением уравнения 8.2 называется функция
 , (8.3)
, (8.3)
как семейство интегральных кривых на плоскости, зависящих от произвольной постоянной , и удовлетворяющая условию 8.2.
, и удовлетворяющая условию 8.2.
 , (8.3)
, (8.3) как семейство интегральных кривых на плоскости, зависящих от произвольной постоянной
 , и удовлетворяющая условию 8.2.
, и удовлетворяющая условию 8.2.Н а п р и м е р: убедимся в том, что функция  – общее решение уравнения
– общее решение уравнения 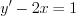 .
.
Найдем производную этой функции: .
.
Подставим значения и
и  в уравнение
в уравнение 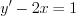 и получим:
и получим:
 ,
,  .
.
 – общее решение уравнения
– общее решение уравнения 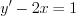 .
. Найдем производную этой функции:
 .
. Подставим значения
 и
и  в уравнение
в уравнение 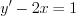 и получим:
и получим:  ,
,  .
.Если общее решение уравнения получено в неявном виде
 , (8.4)
, (8.4)
то его называют общим интегралом.
 , (8.4)
, (8.4) то его называют общим интегралом.
Н а п р и м е р,  – общий интеграл уравнения
– общий интеграл уравнения  .
.
 – общий интеграл уравнения
– общий интеграл уравнения  .
.Решить задачу Коши – значит найти интегральную кривую, проходящую через заданную точку  или иначе найти частное решение
или иначе найти частное решение
 , (8.5)
, (8.5)
удовлетворяющее начальным условиям .
.
 или иначе найти частное решение
или иначе найти частное решение  , (8.5)
, (8.5) удовлетворяющее начальным условиям
 .
.Некоторые виды уравнений первого порядка
1. Дифференциальное уравнение с разделенными переменными имеет вид:
 . (8.6)
. (8.6) Чтобы решить уравнение 8.6, необходимо проинтегрировать его обе части.
Н а п р и м е р, решим уравнение :
:
 ,
,  .
.
Н а п р и м е р, решим уравнение
 :
:  ,
,  .
.2. Дифференциальное уравнение с разделяющимися переменными имеет вид:
 . (8.7)
. (8.7)Чтобы решить уравнение 8.7, необходимо разделить переменные и проинтегрировать обе его части.
3. Дифференциальное однородное уравнение имеет вид:
 , (8.8)
, (8.8) где
 и
и  однородные функции одного и того же порядка:
однородные функции одного и того же порядка:  и
и  .
.Н а п р и м е р:  – однородная функция первого порядка, так как
– однородная функция первого порядка, так как  ; функция
; функция  не является однородной.
не является однородной.
 – однородная функция первого порядка, так как
– однородная функция первого порядка, так как  ; функция
; функция  не является однородной.
не является однородной.4. Дифференциальное линейное уравнение имеет вид:
 . (8.10)
. (8.10)Пример 1. Решите уравнение  .
.
Решение. Поскольку , то запишем данное уравнение так:
, то запишем данное уравнение так:
 ,
,  .
.
Получили уравнение вида 8.6 с разделенными переменными.
Интегрируя обе его части, найдем общее решение 8.3:
 .
. Решение. Поскольку
 , то запишем данное уравнение так:
, то запишем данное уравнение так:  ,
,  .
. Получили уравнение вида 8.6 с разделенными переменными.
Интегрируя обе его части, найдем общее решение 8.3:
 ,
,  ,
,  .
.Ответ:  .
.
 .
.Пример 2. Найдите частное решение уравнение  , если
, если  .
.
Решение. Разделим переменные:
 , если
, если  .
. Решение. Разделим переменные:
Пример 3. Решите уравнение  .
.
 .
. Решение. Запишем уравнение в виде  .
.
Функции и
и  являются однородными функциями первого порядка, так как
являются однородными функциями первого порядка, так как
 , и
, и  .
.
Следовательно, имеем однородное дифференциальное уравнение первого порядка 8.8.
Полагая ,
,  , получим:
, получим:
 ,
,  ,
,  ,
,  ,
,  .
.
Разделим переменные и проинтегрируем полученное равенство:
 .
. Функции
 и
и  являются однородными функциями первого порядка, так как
являются однородными функциями первого порядка, так как  , и
, и  .
. Следовательно, имеем однородное дифференциальное уравнение первого порядка 8.8.
Полагая
 ,
,  , получим:
, получим: ,
,  ,
,  ,
,  ,
,  .
. Разделим переменные и проинтегрируем полученное равенство:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. Учитывая, что
 , получим:
, получим:  ,
, 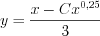 .
. Ответ:
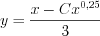 .
. Пример 4. Решите уравнение  .
.
Решение. Имеем линейное уравнение 8.10 .
Полагая ,
,  , получим:
, получим:
 ,
,  .
.
Сгруппируем слагаемые, содержащие множитель , и вынесем его из скобки:
, и вынесем его из скобки:
 ,
,  .
.
Если положим , то получим
, то получим
 .
.
Запишем систему уравнений:
 .
. Решение. Имеем линейное уравнение 8.10 .
Полагая
 ,
,  , получим:
, получим:  ,
,  .
. Сгруппируем слагаемые, содержащие множитель
 , и вынесем его из скобки:
, и вынесем его из скобки:  ,
,  .
. Если положим
 , то получим
, то получим  .
. Запишем систему уравнений:

Решим первое уравнение системы:
 ,
,  ,
,  ,
,  (произвольная постоянная тут всегда равна нулю),
(произвольная постоянная тут всегда равна нулю),  .
.
 ,
,  ,
,  ,
,  (произвольная постоянная тут всегда равна нулю),
(произвольная постоянная тут всегда равна нулю),  .
.Подставим полученное значение  во второе уравнение системы и решим его:
во второе уравнение системы и решим его:
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 во второе уравнение системы и решим его:
во второе уравнение системы и решим его:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.Так как  , то получим:
, то получим:
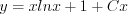 .
.
Ответ: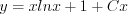 .
.
 , то получим:
, то получим: 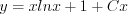 .
. Ответ:
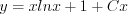 .
.1. Уравнение  может и не содержать переменных
может и не содержать переменных  и (или)
и (или)  , но обязательно должно содержать
, но обязательно должно содержать  .
.
 может и не содержать переменных
может и не содержать переменных  и (или)
и (или)  , но обязательно должно содержать
, но обязательно должно содержать  .
.2. Поскольку  , то дифференциальные уравнения можно записывать и иначе.
, то дифференциальные уравнения можно записывать и иначе.
 , то дифференциальные уравнения можно записывать и иначе.
, то дифференциальные уравнения можно записывать и иначе. Н а п р и м е р: уравнение  запишем так:
запишем так:  ,
,  .
.
 запишем так:
запишем так:  ,
,  .
.