Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
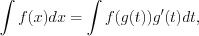 (7.24)
(7.24)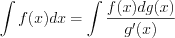 . (7.25)
. (7.25)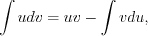 (7.26)
(7.26)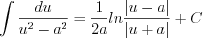 (7.18)
(7.18) 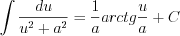 (7.19)
(7.19) 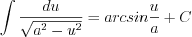 (7.20)
(7.20) 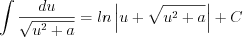 (7.21)
(7.21) 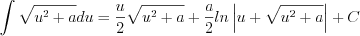 (7.22)
(7.22) 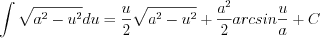 (7.23)
(7.23)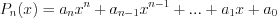
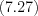
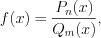 (7.28)
(7.28)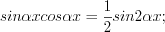 (7.30)
(7.30)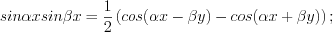 (7.31)
(7.31)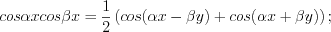 (7.32)
(7.32)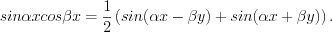 (7.33)
(7.33)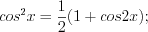 (7.34)
(7.34)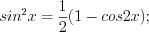 (7.35)
(7.35)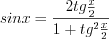 (7.36) и
(7.36) и 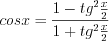 (7.37)
(7.37)
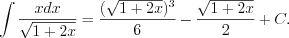
 ,
,  .
.  ,
,  ,
,  ,
, ,
,  .
.
1. Метод подстановки
Подстановка выполняется по формуле:
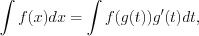 (7.24)
(7.24)где 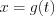 – дифференцируемая функция переменной
– дифференцируемая функция переменной 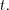
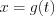 – дифференцируемая функция переменной
– дифференцируемая функция переменной 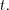
Этот метод в отдельных случаях позволяет свести интеграл к табличному.
2. Метод изменения формы дифференциала
Преобразовать дифференциал можно по формуле:
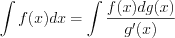 . (7.25)
. (7.25)Этот метод в отдельных случаях позволяет свести интеграл к табличному.
3. Метод интегрирования по частям
Метод интегрирования по частям применяют в случае, когда подынтегральная функция является трансцендентной функцией или представляет собою произведение алгебраической и трансцендентной функций.
Н а п р и м е р: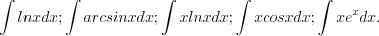
Н а п р и м е р:
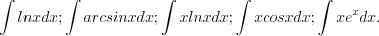
Формула интегрирования по частям:
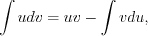 (7.26)
(7.26)где 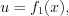 а
а 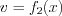 – дифференцируемые функции.
– дифференцируемые функции.
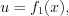 а
а 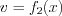 – дифференцируемые функции.
– дифференцируемые функции.В качестве  обычно выбирается функция, которая упрощается дифференцированием, а в качестве
обычно выбирается функция, которая упрощается дифференцированием, а в качестве 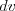 – оставшаяся часть подынтегрального выражения, обязательно содержащая
– оставшаяся часть подынтегрального выражения, обязательно содержащая 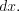
 обычно выбирается функция, которая упрощается дифференцированием, а в качестве
обычно выбирается функция, которая упрощается дифференцированием, а в качестве 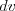 – оставшаяся часть подынтегрального выражения, обязательно содержащая
– оставшаяся часть подынтегрального выражения, обязательно содержащая 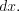
В отдельных случаях искомый интеграл находится из уравнения, полученного в результате интегрирования по частям.
Н а п р и м е р,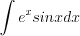 и
и 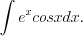
Н а п р и м е р,
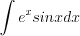 и
и 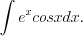
Интегрирование выражений, содержащих квадратный трехчлен
Интегрирование некоторых функций, содержащих квадратный трехчлен, можно выполнить по формулам 7.18,7.19,7.20,7.21,7.22 и 7.23 , если дополнить квадратный трехчлен до квадрата суммы или квадрата разности в общем случае так:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 ,
,  ,
,  ,
,  ,
,  .
.Таблица 2. Неопределенные интегралы
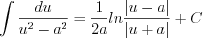 (7.18)
(7.18) 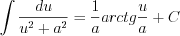 (7.19)
(7.19) 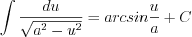 (7.20)
(7.20) 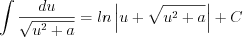 (7.21)
(7.21) 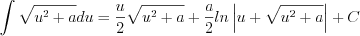 (7.22)
(7.22) 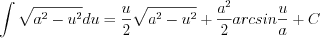 (7.23)
(7.23)Интегрирование рациональных дробей
Многочленом степени n от одной переменной  называют выражение вида
называют выражение вида
 называют выражение вида
называют выражение вида 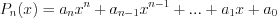
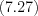
при 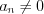 и
и 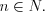
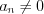 и
и 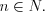
Числа 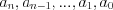 называют коэффициентами многочлена, при этом число
называют коэффициентами многочлена, при этом число 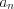 называют старшим коэффициентом многочлена, а число
называют старшим коэффициентом многочлена, а число 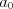 – свободным членом. Коэффициенты многочлена, за исключением его старшего коэффициента, могут быть равны нулю.
– свободным членом. Коэффициенты многочлена, за исключением его старшего коэффициента, могут быть равны нулю.
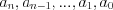 называют коэффициентами многочлена, при этом число
называют коэффициентами многочлена, при этом число 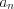 называют старшим коэффициентом многочлена, а число
называют старшим коэффициентом многочлена, а число 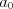 – свободным членом. Коэффициенты многочлена, за исключением его старшего коэффициента, могут быть равны нулю.
– свободным членом. Коэффициенты многочлена, за исключением его старшего коэффициента, могут быть равны нулю.Н а п р и м е р: 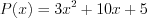 – многочлен второй степени.
– многочлен второй степени.
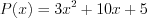 – многочлен второй степени.
– многочлен второй степени.Многочлен вида 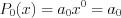 называют многочленом нулевой степени, а если
называют многочленом нулевой степени, а если 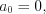 то имеем нулевой многочлен.
то имеем нулевой многочлен.
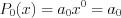 называют многочленом нулевой степени, а если
называют многочленом нулевой степени, а если 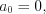 то имеем нулевой многочлен.
то имеем нулевой многочлен. Н а п р и м е р, 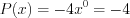 – многочлен нулевой степени, а
– многочлен нулевой степени, а 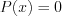 – нулевой многочлен.
– нулевой многочлен.
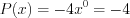 – многочлен нулевой степени, а
– многочлен нулевой степени, а 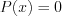 – нулевой многочлен.
– нулевой многочлен.Корнем многочлена 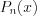 называют такое число
называют такое число 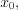 что
что 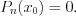
Число с называют корнем кратности многочлена
многочлена 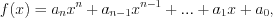
если справедливо равенство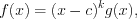
где – многочлен степени
– многочлен степени 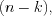
 и
и  – натуральные числа
– натуральные числа 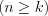 и
и 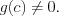
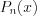 называют такое число
называют такое число 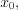 что
что 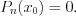
Число с называют корнем кратности
 многочлена
многочлена 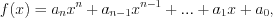
если справедливо равенство
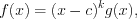
где
 – многочлен степени
– многочлен степени 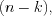
 и
и  – натуральные числа
– натуральные числа 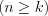 и
и 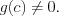
Если 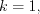 то говорят, что число
то говорят, что число  – простой корень многочлена.
– простой корень многочлена.
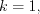 то говорят, что число
то говорят, что число  – простой корень многочлена.
– простой корень многочлена.Н а п р и м е р, числа  и
и  простые корни многочлена
простые корни многочлена 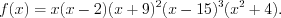
Число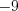 двукратный корень, а число
двукратный корень, а число  его трехкратный корень.
его трехкратный корень.
 и
и  простые корни многочлена
простые корни многочлена 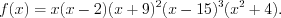
Число
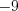 двукратный корень, а число
двукратный корень, а число  его трехкратный корень.
его трехкратный корень.Дробной рациональной функцией называют функцию вида
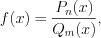 (7.28)
(7.28)где 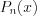 и
и 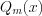 – многочлены степеней
– многочлены степеней  и
и  соответственно.
соответственно.
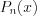 и
и 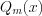 – многочлены степеней
– многочлены степеней  и
и  соответственно.
соответственно.Если разложить многочлен-знаменатель на множители 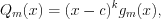 то правильную дробь 7.28 можно представить в виде суммы простейших дробей по формуле:
то правильную дробь 7.28 можно представить в виде суммы простейших дробей по формуле:
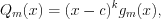 то правильную дробь 7.28 можно представить в виде суммы простейших дробей по формуле:
то правильную дробь 7.28 можно представить в виде суммы простейших дробей по формуле: 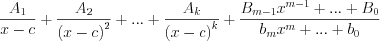 , (7.29)
, (7.29)
где числа 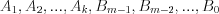 – неопределенные коэффициенты.
– неопределенные коэффициенты.
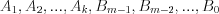 – неопределенные коэффициенты.
– неопределенные коэффициенты.Интегрирование тригонометрических функций
1. Если интеграл имеет вид 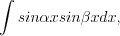 или
или 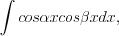 или
или 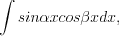 то подынтегральную функцию необходимо преобразовать с помощью одной из формул:
то подынтегральную функцию необходимо преобразовать с помощью одной из формул:
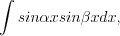 или
или 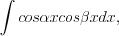 или
или 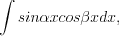 то подынтегральную функцию необходимо преобразовать с помощью одной из формул:
то подынтегральную функцию необходимо преобразовать с помощью одной из формул: 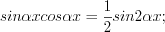 (7.30)
(7.30)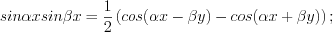 (7.31)
(7.31)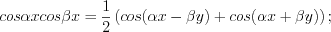 (7.32)
(7.32)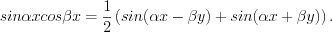 (7.33)
(7.33)2. Если интеграл имеет вид 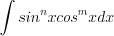 и числа
и числа  и
и  четные, то подынтегральную функцию необходимо преобразовать с помощью формул понижения степени:
четные, то подынтегральную функцию необходимо преобразовать с помощью формул понижения степени:
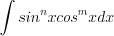 и числа
и числа  и
и  четные, то подынтегральную функцию необходимо преобразовать с помощью формул понижения степени:
четные, то подынтегральную функцию необходимо преобразовать с помощью формул понижения степени: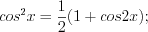 (7.34)
(7.34)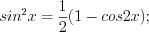 (7.35)
(7.35)Если хотя бы одно из чисел  или
или  нечетное, то необходимо отделить от нечетной степени один множитель.
нечетное, то необходимо отделить от нечетной степени один множитель.
 или
или  нечетное, то необходимо отделить от нечетной степени один множитель.
нечетное, то необходимо отделить от нечетной степени один множитель.3. Если интеграл имеет вид 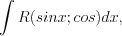 где
где  – рациональная функция от
– рациональная функция от 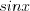 и
и 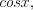 то необходимо использовать подстановку
то необходимо использовать подстановку 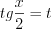 и с учетом формул
и с учетом формул
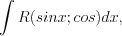 где
где  – рациональная функция от
– рациональная функция от 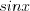 и
и 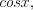 то необходимо использовать подстановку
то необходимо использовать подстановку 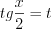 и с учетом формул
и с учетом формул 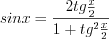 (7.36) и
(7.36) и 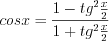 (7.37)
(7.37)записать: 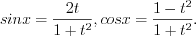
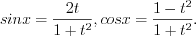
Пример 1. Найдите интеграл 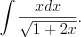
Решение. Применим метод подстановки 7.24 .
Положим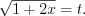
Запишем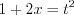 и продифференцируем это равенство:
и продифференцируем это равенство:
 ,
,  ,
,  .
.
Переходя к новой переменной, получим интеграл:
 ,
,  ,
,  .
.
Возвращаясь к переменной найдем данный интеграл:
найдем данный интеграл:
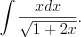
Решение. Применим метод подстановки 7.24 .
Положим
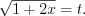
Запишем
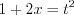 и продифференцируем это равенство:
и продифференцируем это равенство:  ,
,  ,
,  .
. Переходя к новой переменной, получим интеграл:
 ,
,  ,
,  .
. Возвращаясь к переменной
 найдем данный интеграл:
найдем данный интеграл: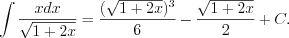
Ответ:  .
.
 .
.Воспользуемся табличным интегралом  и получим:
и получим:
 .
.
 и получим:
и получим:  .
. Ответ:  .
.
 .
.Пример 3. Найдите интеграл  .
.
Решение. Применим формулу интегрирования по частям 7.26.
Положим , а
, а 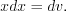
Дифференцируя первое равенство, получим:
 , откуда
, откуда  .
.
Интегрируя второе равенство (здесь произвольная постоянная всегда равна нулю), получим:
 , откуда
, откуда  .
.
Найдем интеграл:
 ,
,
 .
. Решение. Применим формулу интегрирования по частям 7.26.
Положим
 , а
, а 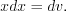
Дифференцируя первое равенство, получим:
 , откуда
, откуда  .
. Интегрируя второе равенство (здесь произвольная постоянная всегда равна нулю), получим:
 , откуда
, откуда  .
. Найдем интеграл:
 ,
,  ,
,  .
. Ответ:  .
.
 .
.Пример 4. Найдите интеграл 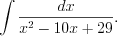
Решение. Преобразуем квадратный трехчлен:
 ,
,
 ,
,
 .
.
Согласно формуле 7.19 получим:
 ,
,  .
.
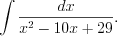
Решение. Преобразуем квадратный трехчлен:
 ,
,  ,
,  .
. Согласно формуле 7.19 получим:
 ,
,  .
.Ответ:  .
.
 .
.Пример 5. Найдите интеграл 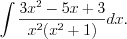
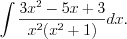
Решение. По формуле 7.29 представим подынтегральную функцию в виде суммы простейших дробей:
 ,
,
 ,
,  ,
,  ,
, откуда 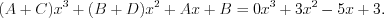
Приравнивая коэффициенты многочленов при одинаковых степенях переменных, получим систему уравнений:
 ,
,  ,
,  ,
,  .
.
Тогда: ,
,  ,
,  ,
, 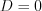 .
.
Найдем сумму интегралов:
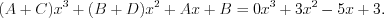
Приравнивая коэффициенты многочленов при одинаковых степенях переменных, получим систему уравнений:
 ,
,  ,
,  ,
,  .
. Тогда:
 ,
,  ,
,  ,
, 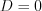 .
. Найдем сумму интегралов:
 ,
, ,
,  .
.Ответ:  .
.
 .
. Пример 6. Найдите интеграл  .
.
Решение. Преобразуем подынтегральную функцию по формулам 7.30 и 7.33 :
 ,
,
 ,
,
 ,
,
 .
.
Интегрируя это выражение, получим:
 ,
,
 .
.
 .
. Решение. Преобразуем подынтегральную функцию по формулам 7.30 и 7.33 :
 ,
,  ,
,  ,
,  .
. Интегрируя это выражение, получим:
 ,
, .
.Ответ:  .
.
 .
.1. В общем случае, если 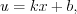 то
то
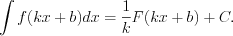
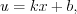 то
то 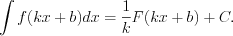
2. Если дробь 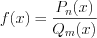 неправильная, то необходимо предварительно выделить ее целую часть, например, разделив многочлены уголком.
неправильная, то необходимо предварительно выделить ее целую часть, например, разделив многочлены уголком.
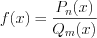 неправильная, то необходимо предварительно выделить ее целую часть, например, разделив многочлены уголком.
неправильная, то необходимо предварительно выделить ее целую часть, например, разделив многочлены уголком. 3. Деление многочленов выполняют аналогично делению целых чисел:
делят старший член многочлена-делимого на старший член многочлена-делителя, затем частное умножают на многочлен-делитель и полученное произведение вычитают из многочлена-делимого.
Многочлен-первый остаток аналогичным образом делят на многочлен-делитель.
Деление продолжают до тех пор пока не получат остаток нуль или степень многочлена-остатка не будет меньше степени многочлена-делителя.
делят старший член многочлена-делимого на старший член многочлена-делителя, затем частное умножают на многочлен-делитель и полученное произведение вычитают из многочлена-делимого.
Многочлен-первый остаток аналогичным образом делят на многочлен-делитель.
Деление продолжают до тех пор пока не получат остаток нуль или степень многочлена-остатка не будет меньше степени многочлена-делителя.
4. Если первообразная 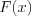 функции
функции  не является элементарной функцией, то соответствующий интеграл
не является элементарной функцией, то соответствующий интеграл 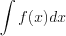 называют «неберущимся».
называют «неберущимся».
П р и м е р ы «неберущихся» интегралов:
 ;
;  ;
;  ;
;  ;
;  ;
;
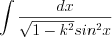 при
при 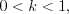
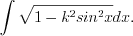
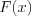 функции
функции  не является элементарной функцией, то соответствующий интеграл
не является элементарной функцией, то соответствующий интеграл 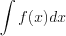 называют «неберущимся».
называют «неберущимся». П р и м е р ы «неберущихся» интегралов:
 ;
;  ;
;  ;
;  ;
;  ;
;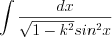 при
при 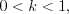
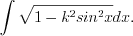
Интегрирование по частям
Изменение дифференциала


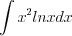
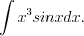
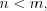 то дробь
то дробь  то неправильная.
то неправильная.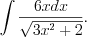
 ,
, 
