Максимумом (минимумом)
функции 
называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
Максимум и минимум функции называются экстремумом функции .
Значения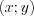 
, при котором достигается экстремум, называется
точкой экстремума .
Критическими точками
первого порядка функции называют точки, в которых все ее частные производные первого порядка равны нулю или не существуют.
Чтобы найти точки экстремума функции , необходимо:
1) найти частные производные первого порядка функции;
2) найти критические точки функции, решая систему уравнений 
и 
;
3) найти частные производные второго порядка функции;
4) найти значения вторых производных в критической точке 
:
,
, 
;
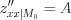5) найти определитель 
;
6) если 
, то экстремум в точке есть; если 
, то экстремума в этой точке нет;
7) если 
, то имеем точку максимума, а если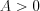 
– точку минимума.
Условный экстремум
Алгоритм отыскания условного экстремума функции при наличии уравнения связи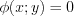 
.
Метод неопределенных множителей Лагранжа:
1) запишем функцию Лагранжа 
,
где 
– неопределенный множитель;
2) найдем частные производные функции Лагранжа: 
, 
,
;
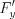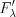3) решая систему уравнени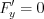й 
, 
и 
, найдем значения , 
и 
;
4) найдем дифференциал второго порядка функции Лагранжа: 
;
5) определим знак 
для системы значений , и при условии, что
;
6) если 
, то функция имеет условный максимум, а если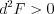 
, то функция имеет условный минимум.
.1. Найдем частные производные первого порядка:
, 
.
2. Найдем критические точки функции, решая систему уравнений:
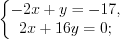
Получим: 
.
3. Найдем частные производные второго порядка:
, 
, 
.
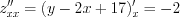4. Найдем значения вторых производных в критической точке:
,
, 
.
5. Найдем определитель
.
6. Так как , то критическая точка не является точкой экстремума.
Пример 2.
Найдите экстремумы функции 
при условии, что 
.
Решение
. 1. Запишем уравнение связи в виде:
.
Найдем полный дифференциал: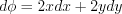 
.
2. Составим функцию Лагранжа 6.31:
.
3. Найдем частные производные функции Лагранжа:
; 
; 
.
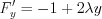4. Найдем значения , и , решая систему уравнений:
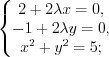
Выразим переменные и в первых двух уравнениях системы:
; 
.
Подставим эти значения в третье уравнение системы:
, 
, 
, 
.
Получим: 
, 
, 
; 
, 
, 
.
4. Найдем частные производные второго порядка функции Лагранжа: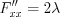
;
;
.
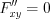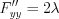Запишем дифференциал второго порядка функции Лагранжа:
.
5. Определим знак для каждой системы значений , и .
Если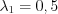 
, то , 
.
Тогда: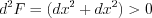 
.
Следовательно, имеем точку условного минимума:
.
Если , то 
, .
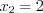Тогда: 
.
Следовательно, имеем точку условного максимума:
.
6. Найдем значения функции в полученных точках: 
; 
.
;
.Если функция непрерывна и ограничена в некоторой замкнутой области, то своего наибольшего и наименьшего значения она может достигать или в критических точках, принадлежащих данной области, или на границе области.
Алгоритм отыскания наибольшего и наименьшего значений функции в заданной области:
1) находим критические точки функции и, если они принадлежат заданной области, вычисляем значения функции в этих точках;
2) находим наибольшее и наименьшее значения функции на границе области;
3) сравнивая все полученные значения функции, определяем наибольшее и наименьшее из них.
На границе области функция является функцией одной переменной 
или 
, следовательно, ее исследование проводят согласно алгоритму, приведенному в п. 6.2.