Теоремы о дифференцируемых функциях
и 
, которые непрерывны на отрезке ![LaTeX formula: [a;b]](/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png "[a;b]")
и дифференцируемы на интервале 
.1. Теорема Ферма : если функция
в точке 
имеет локальный экстремум, то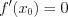 
. Геометрический смысл теоремы: касательная к графику функции в точке
параллельна оси абсцисс.
2. Теорема Лагранжа: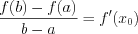 
, где .
Геометрический смысл теоремы: касательная к графику функции в точке параллельна секущей, соединяющей концы графика этой функции.
3. Теорема Ролля: если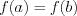 
и , то .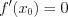
Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.
4. Теорема Коши: если , то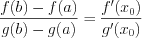 
.
Исследование функции с помощью первой производной
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке 
, то функция возрастает на этом промежутке;
б) если 
, то функция убывает на этом промежутке.
Экстремум функции
Максимумом (минимумом)
функции 
называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4).
Максимум и минимум функции называются
экстремумом функции
. Значение аргумента, при котором достигается экстремум, называется
точкой экстремума
. На рисунке 6.4 значения 
,
,
,
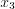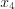и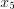 
являются точками экстремума рассматриваемой функции.
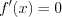.Алгоритм нахождения точек экстремума функции:
1) находим область определения функции ;
2) находим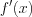 
;
3) находим критические точки функции, решая уравнение ;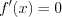
4) наносим критические точки на область определения функции;
5) определяем знак производной функции на полученных промежутках;
6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.
Рассмотрим функцию на отрезке . Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.
Алгоритм нахождения наибольшего и наименьшего
значений
функции на заданном отрезке:
1) находим ;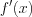
2) находим критические точки функции, решая уравнение ;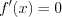
3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Исследование функции с помощью второй производной
Критическими точками второго рода
функции называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.
Критические точки второго рода функции находят, решая уравнение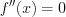 
.
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба графика функции.
Если на некотором промежутке выполняется неравенство 
, то функция вогнута
на этом промежутке, а если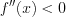 
, то функция
выпукла
на этом промежутке.
.
. Найдем критические точки:
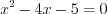, откуда 
, 
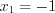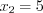.Нанесем числа
и 
на координатную прямую и установим знаки производной на полученных промежутках: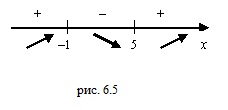 
и 
функция возрастает. На промежутке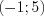 
функция убывает. Точки экстремума: 
, 
. 
. Решение. 1. Используя таблицу производных найдем первую производную функции:
.2. Используя таблицу производных найдем вторую производную функции:
.3. Найдем критические точки второго рода:
, 
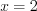.4. Нанесем точку
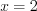на область определения данной функции и установим знаки ее второй производной на полученных промежутках: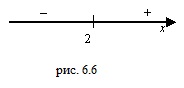 
функция выпукла вверх; на промежутке 
функция выпукла вниз; 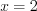– точка перегиба графика функции.
на отрезке ![LaTeX formula: [1;e]](/uploads/formulas/eb6e890201c9d8770f7e173603dbc77ae36dc386.1.1.png "[1;e]")
.Решение. 1. По формуле
найдем производную данной функции: 
.2. Найдем критические точки функции, решая уравнение
, откуда 
, 
.3. Найдем значение функции на концах отрезка
и в критической точке , поскольку она принадлежит данному отрезку: 
, 
, 
.
Ответ
: 
, 
.
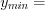
. 1. Находим область определения функции.
2. Определяем, является ли функция четной или нечетной.
3. Выясняем, является ли функция периодической.
4. Находим точки пересечения графика функции с осью ординат.
5. Находим нули функции (точки пересечения графика функции с осью абсцисс).
6. Проводим исследование функции с помощью первой производной:
а) находим критические точки первого рода;
б) находим промежутки возрастания и убывания функции;
в) находим точки экстремума функции и значение функции в точках экстремума.
7. Проводим исследование функции с помощью второй производной:
а) находим критические точки второго рода;
б) находим промежутки выпуклости и вогнутости функции;
в) находим точки перегиба графика функции.
8. Находим асимптоты графика функции.
9. Строим график функции.
10. Находим промежутки знакопостоянства функции: промежутки, на которых функция положительна и промежутки, на которых функция отрицательна.
11. Находим область значений функции.