Асимптотой линии называют прямую, к которой неограниченно приближается данная линия, когда ее точка неограниченно удаляется от начала координат.
Виды асимптот:
1) вертикальные
– параллельные оси 
;
2) наклонные
– пересекающие ось ;
3) горизонтальные
– параллельные оси 
.
Например, график функции 
имеет две горизонтальные асимптоты 
(рис. 5.11) , а график функции 
– вертикальную асимптоту 
и наклонную асимптоту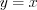 
(рис. 5.12).
1. Уравнение вертикальной асимптоты
графика функции 
имеет вид 
, при условии, что выполняется хотя бы одно из условий:
, 
.
2. Уравнение наклонной асимптоты графика функции имеет вид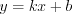 
, где
, (5.28)
. (5.29)
Пример 1.
Найдите асимптоты функции 
.
Решение
. 1. Найдем область определения функции:
.
2. Найдем вертикальную асимптоту графика функции. Так как точка 
является точкой разрыва функции, то прямая является вертикальной асимптотой ее графика.
Действительно, 
.
3. Уравнение наклонной асимптоты графика функции будем искать в виде .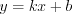
По формулам 5.28 и 5.29 найдем 
и 
:
; 
.
Наклонная асимптота: .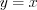
, .
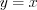, то получим
горизонтальную асимптоту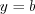 
.