Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (4.36)
. (4.36) . (4.37)
. (4.37) . (4.38)
. (4.38) и
и  ,
, . (4.39)
. (4.39) . (4.40)
. (4.40) . (4.41)
. (4.41) . (4.42)
. (4.42) . (4.43)
. (4.43) . (4.44)
. (4.44) . (4.45)
. (4.45) . (4.46)
. (4.46)
 и
и  .
.  .
.  ,
,  .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
.
 .
.
Взаимное расположение плоскостей
Рассмотрим две плоскости  и
и  с нормальными векторами
с нормальными векторами 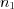 и
и 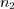 .
.
 и
и  с нормальными векторами
с нормальными векторами 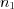 и
и 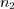 .
.1. Плоскости параллельны, если
 . (4.36)
. (4.36)Например, плоскости  и
и  параллельны.
параллельны.
 и
и  параллельны.
параллельны.2. Плоскости перпендикулярны, если
 . (4.37)
. (4.37)3. Угол  между плоскостями находят по формуле:
между плоскостями находят по формуле:
 между плоскостями находят по формуле:
между плоскостями находят по формуле:  . (4.38)
. (4.38)Взаимное расположение прямых
Рассмотрим две прямые, записанные в каноническом виде
 и
и  ,
,где 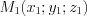 и
и 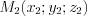 – точки, принадлежащие этим прямым, а
– точки, принадлежащие этим прямым, а  и
и  – направляющие векторы этих прямых.
– направляющие векторы этих прямых.
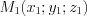 и
и 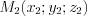 – точки, принадлежащие этим прямым, а
– точки, принадлежащие этим прямым, а  и
и  – направляющие векторы этих прямых.
– направляющие векторы этих прямых.1. Прямые параллельны, если параллельны их направляющие векторы:
 . (4.39)
. (4.39)Например, прямые  и
и  параллельны.
параллельны.
 и
и  параллельны.
параллельны.2. Прямые перпендикулярны, если перпендикулярны их направляющие векторы:
 . (4.40)
. (4.40)Например, прямые  и
и  перпендикулярны.
перпендикулярны.
 и
и  перпендикулярны.
перпендикулярны.3. Угол между прямыми находят по формуле:
между прямыми находят по формуле:
 между прямыми находят по формуле:
между прямыми находят по формуле:  . (4.41)
. (4.41)4. Прямые скрещиваются, если они лежат в разных плоскостях, то есть векторы  ,
,  и
и  не компланарны:
не компланарны:
 ,
,  и
и  не компланарны:
не компланарны: . (4.42)
. (4.42)Взаимное расположение прямой и плоскости
Рассмотрим прямую  и плоскость
и плоскость  .
.
 и плоскость
и плоскость  .
. 1. Прямая параллельна плоскости, если
 . (4.43)
. (4.43)Например, прямая  параллельна плоскости
параллельна плоскости  .
.
 параллельна плоскости
параллельна плоскости  .
.2. Прямая перпендикулярна плоскости, если
 . (4.44)
. (4.44)Например, прямая  перпендикулярна плоскости
перпендикулярна плоскости  .
.
 перпендикулярна плоскости
перпендикулярна плоскости  .
.3. Угол между прямой и плоскостью находят по формуле:
между прямой и плоскостью находят по формуле:
 между прямой и плоскостью находят по формуле:
между прямой и плоскостью находят по формуле: . (4.45)
. (4.45)Расстояние от точки 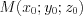 до плоскости
до плоскости  с нормальным вектором
с нормальным вектором  находят по формуле:
находят по формуле:
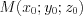 до плоскости
до плоскости  с нормальным вектором
с нормальным вектором  находят по формуле:
находят по формуле:  . (4.46)
. (4.46)Пример 1. Найдите угол между прямыми  и
и  .
.
 и
и  .
. и
и  .
.2. Найдем скалярное произведение направляющих векторов прямых:
 .
. 3. Найдем длины направляющих векторов прямых:
 ,
,  .
.Ответ:  .
.
 .
. Пример 2. Найдите произведение значений и
и , при которых прямая
, при которых прямая  перпендикулярна плоскости
перпендикулярна плоскости  .
.
 и
и , при которых прямая
, при которых прямая  перпендикулярна плоскости
перпендикулярна плоскости  .
.Решение. Согласно условию задачи запишем:
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.Тогда  и
и  , откуда
, откуда  ,
,  , а
, а  .
.
 и
и  , откуда
, откуда  ,
,  , а
, а  .
.Ответ: 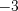 .
.
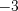 .
. Пример 3. Найдите расстояние между плоскостями  и
и  .
.
 и
и  .
.Решение. 1. Запишем нормальные векторы данных плоскостей:  ,
,  .
.
 ,
,  .
. 2. Найдем любую точку, принадлежащую плоскости  .
.
 .
. Например, полагая  , а
, а  , получим
, получим 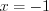 .
.
 , а
, а  , получим
, получим 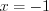 .
. 3. Найдем расстояние от точки  до плоскости
до плоскости  .
.
 до плоскости
до плоскости  .
.  .
.Ответ:  .
.
 .
.1. Скалярное произведение векторов  и
и  находят по формуле:
находят по формуле:  .
.
 и
и  находят по формуле:
находят по формуле:  .
.2. Длину вектора  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле: .
.




