Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 .
.  .
. .
. .
. ,
, ,
, .
. ,
,  ,
,  .
. .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 .
. .
.
 .
.
1. Решение систем линейных уравнений методом Крамера
Чтобы решить систему линейных уравнений, содержащую  уравнений и
уравнений и  переменных, методом Крамера, необходимо:
переменных, методом Крамера, необходимо:
 уравнений и
уравнений и  переменных, методом Крамера, необходимо:
переменных, методом Крамера, необходимо:1) найти определитель 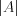 основной матрицы системы;
основной матрицы системы;
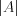 основной матрицы системы;
основной матрицы системы;2) найти определители  (
(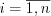 ), полученные в результате замены i-го столбца определителя
), полученные в результате замены i-го столбца определителя 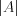 столбцом свободных членов системы;
столбцом свободных членов системы;
 (
(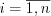 ), полученные в результате замены i-го столбца определителя
), полученные в результате замены i-го столбца определителя 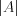 столбцом свободных членов системы;
столбцом свободных членов системы;3) найти значения переменных уравнений системы по формулам , которые называют формулами Крамера.
, которые называют формулами Крамера.
 , которые называют формулами Крамера.
, которые называют формулами Крамера. 2. Решение систем линейных уравнений методом Гаусса
Чтобы решить систему линейных уравнений методом Гаусса, необходимо:
1) составить расширенную матрицу системы;
2) с помощью элементарных преобразований привести ее к трапециевидному виду;
3) на основе полученной матрицы составить и решить систему линейных уравнений;
Чтобы привести матрицу к треугольному виду, можно выполнять следующие элементарные преобразования этой матрицы:
1) умножать и делить ее любою строку на отличное от нуля число;
2) менять местами строки;
3) складывать и вычитать строки;
4) вычеркивать строки, все элементы в которых нули.
3. Решение систем линейных уравнений матричным методом
Систему уравнений, содержащую  уравнений и
уравнений и  переменных, можно записать в виде матричного уравнения:
переменных, можно записать в виде матричного уравнения: 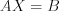 , откуда
, откуда  .
.
 уравнений и
уравнений и  переменных, можно записать в виде матричного уравнения:
переменных, можно записать в виде матричного уравнения: 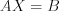 , откуда
, откуда  .
.Чтобы решить систему линейных уравнений матричным методом, необходимо:
1) записать основную матрицу  системы;
системы;
 системы;
системы;2) записать матрицу-столбец  , состоящую из переменных уравнений системы;
, состоящую из переменных уравнений системы;
 , состоящую из переменных уравнений системы;
, состоящую из переменных уравнений системы;3) записать матрицу  , состоящую из столбца свободных членов;
, состоящую из столбца свободных членов;
 , состоящую из столбца свободных членов;
, состоящую из столбца свободных членов;4) найти определитель основной матрицы системы;
5) найти матрицу, обратную матрице  ;
;
 ;
;6) найти матрицу  , умножив матрицу
, умножив матрицу 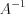 на матрицу
на матрицу  .
.
 , умножив матрицу
, умножив матрицу 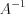 на матрицу
на матрицу  .
.Пример 1. Решите систему линейных уравнений  методом Крамера.
методом Крамера.
 методом Крамера.
методом Крамера.Решение. Вычислим определитель основной матрицы системы:
 .
. Так как  , то решение системы можем найти по формулам Крамера.
, то решение системы можем найти по формулам Крамера.
 , то решение системы можем найти по формулам Крамера.
, то решение системы можем найти по формулам Крамера.Заменим первый столбец определителя 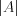 столбцом свободных членов и найдем
столбцом свободных членов и найдем  :
:
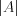 столбцом свободных членов и найдем
столбцом свободных членов и найдем  :
:  .
.Заменим второй столбец определителя 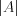 столбцом свободных членов и найдем
столбцом свободных членов и найдем  :
:
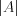 столбцом свободных членов и найдем
столбцом свободных членов и найдем  :
:  .
.Заменим третий столбец определителя 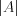 столбцом свободных членов и найдем
столбцом свободных членов и найдем  :
:
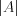 столбцом свободных членов и найдем
столбцом свободных членов и найдем  :
:  .
.Найдем значения переменных:
 ,
, ,
, .
.Проверка: 

Ответ:  ,
,  ,
,  .
.
 ,
,  ,
,  .
.Пример 2. Решите систему линейных уравнений  матричным методом.
матричным методом.
 матричным методом.
матричным методом.Решение. Запишем матрицы системы:
 ,
,  ,
,  .
.Так как  , то решение системы можем найти матричным методом по формуле
, то решение системы можем найти матричным методом по формуле  .
.
 , то решение системы можем найти матричным методом по формуле
, то решение системы можем найти матричным методом по формуле  .
.Матрицу, обратную данной, найдем по формуле:
 .
.По формуле  найдем алгебраические дополнения элементов матрицы
найдем алгебраические дополнения элементов матрицы  :
:
 найдем алгебраические дополнения элементов матрицы
найдем алгебраические дополнения элементов матрицы  :
:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.Получим:

 .
.Ответ:  ,
,  ,
,  .
.
 ,
,  ,
,  .
. Пример 3. Решите систему линейных уравнений  методом Гаусса.
методом Гаусса.
 методом Гаусса.
методом Гаусса.Решение. Запишем расширенную матрицу системы:
 .
.С помощью элементарных преобразований приведем ее к трапециевидному виду:

 .
.Решим систему уравнений: 

Решая уравнение  , получим:
, получим:  .
.
 , получим:
, получим:  .
.Решая уравнение  , получим:
, получим:  ,
,  .
.
 , получим:
, получим:  ,
,  .
. Решая уравнение  , получим:
, получим:  ,
,  .
.
 , получим:
, получим:  ,
,  .
.Ответ:  ,
,  ,
,  .
.
 ,
,  ,
,  .
.1. Методом Крамера и матричным методом можно решать только те системы, которые содержат  уравнений и
уравнений и  переменных.
переменных.
 уравнений и
уравнений и  переменных.
переменных.2. Если определитель 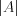 основной матрицы системы равен нулю, то такую систему уравнений нельзя решить методом Крамера и матричным методом.
основной матрицы системы равен нулю, то такую систему уравнений нельзя решить методом Крамера и матричным методом.
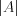 основной матрицы системы равен нулю, то такую систему уравнений нельзя решить методом Крамера и матричным методом.
основной матрицы системы равен нулю, то такую систему уравнений нельзя решить методом Крамера и матричным методом.3. Если матрица, составленная из коэффициентов при переменных системы линейных уравнений, вырождена, то такая система уравнений может не иметь вовсе решений либо иметь бесконечно много решений.
4. Любую совместную систему линейных алгебраических уравнений можно решить методом Гаусса.
Матричный метод
Метод определителей
Метод Гаусса

