Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты

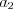

![a_{m} ]; LaTeX formula: a_{m} ];](/uploads/formulas/e13dde6bde8efbfe87b9bc6eb3b1c5125e697823.1.1.png) (12.27)
(12.27)


![b_{n}]; LaTeX formula: b_{n}];](/uploads/formulas/0770e1186e9cb825fa579e4e81bf058cdb660818.1.1.png) (12.28)
(12.28)
 (12.29)
(12.29) (12.30)
(12.30) (12.31)
(12.31)
 (12.32)
(12.32)
 (12.33)
(12.33)
 (12.34)
(12.34)  (12.35)
(12.35) (12.36)
(12.36)  (12.37)
(12.37)

Постановка транспортной задачи в матричной форме по критерию стоимости
В пунктах  находится однородный груз в количествах
находится однородный груз в количествах  единиц соответственно. Этот груз необходимо доставить потребителям
единиц соответственно. Этот груз необходимо доставить потребителям  в количествах
в количествах  единиц соответственно. Известна стоимость перевозки
единиц соответственно. Известна стоимость перевозки  единицы груза от
единицы груза от  -го поставщика (
-го поставщика ( ) к
) к 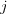 -му
-му  потребителю. Требуется составить такой план перевозок, который полностью удовлетворяет спрос потребителя при минимальных суммарных транспортных издержках.
потребителю. Требуется составить такой план перевозок, который полностью удовлетворяет спрос потребителя при минимальных суммарных транспортных издержках.
 находится однородный груз в количествах
находится однородный груз в количествах  единиц соответственно. Этот груз необходимо доставить потребителям
единиц соответственно. Этот груз необходимо доставить потребителям  в количествах
в количествах  единиц соответственно. Известна стоимость перевозки
единиц соответственно. Известна стоимость перевозки  единицы груза от
единицы груза от  -го поставщика (
-го поставщика ( ) к
) к 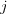 -му
-му  потребителю. Требуется составить такой план перевозок, который полностью удовлетворяет спрос потребителя при минимальных суммарных транспортных издержках.
потребителю. Требуется составить такой план перевозок, который полностью удовлетворяет спрос потребителя при минимальных суммарных транспортных издержках. Матрицы транспортной задачи (ТЗ) имеют вид:
1) матрица запаса груза

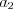

![a_{m} ]; LaTeX formula: a_{m} ];](/uploads/formulas/e13dde6bde8efbfe87b9bc6eb3b1c5125e697823.1.1.png) (12.27)
(12.27)2) матрица потребности в грузе



![b_{n}]; LaTeX formula: b_{n}];](/uploads/formulas/0770e1186e9cb825fa579e4e81bf058cdb660818.1.1.png) (12.28)
(12.28)3) матрица тарифов перевозок

 (12.29)
(12.29)4) матрица перевозок:
 (12.30)
(12.30)Экономико-математическая модель задачи
Целевая функция:
 (12.31)
(12.31)Система ограничений:

 (12.32)
(12.32)
 (12.33)
(12.33)
 (12.34)
(12.34)Для того чтобы ТЗ имела допустимые планы, необходимо и достаточно выполнение равенства:
 (12.35)
(12.35)Модели транспортной задачи
Модель ТЗ называется закрытой, если суммарный запас груза у поставщиков равен суммарному спросу потребителей, т.е. выполняется условие 12.35.
Модель ТЗ называется открытой, если суммарный запас груза у поставщиков не равен суммарному спросу потребителей, т.е. выполняется одно из условий:
 (12.36)
(12.36) (12.37)
(12.37)В процессе решения ТЗ открытую модель всегда необходимо преобразовывать в закрытую.
В случае, когда выполняется условие 12.36, необходимо ввести фиктивного  потребителя, потребность в грузе которого составит
потребителя, потребность в грузе которого составит  а все тарифы перевозок от поставщиков к фиктивному потребителю будут равны нулю.
а все тарифы перевозок от поставщиков к фиктивному потребителю будут равны нулю.
 потребителя, потребность в грузе которого составит
потребителя, потребность в грузе которого составит  а все тарифы перевозок от поставщиков к фиктивному потребителю будут равны нулю.
а все тарифы перевозок от поставщиков к фиктивному потребителю будут равны нулю. В случае, когда выполняется условие 12.37, необходимо ввести фиктивного поставщика  , запас груза которого составит
, запас груза которого составит а все тарифы перевозок от фиктивного поставщика к потребителям будут равны нулю.
а все тарифы перевозок от фиктивного поставщика к потребителям будут равны нулю.
 , запас груза которого составит
, запас груза которого составит а все тарифы перевозок от фиктивного поставщика к потребителям будут равны нулю.
а все тарифы перевозок от фиктивного поставщика к потребителям будут равны нулю.Построение исходного опорного плана
Построение опорного плана ТЗ будем выполнять в распределительной таблице по правилу «минимального элемента»:
1) выбираем клетку с минимальным тарифом и записываем в нее максимально возможное значение поставки;
2) из рассмотрения исключаем поставщика (и соответствующую ему строку), запасы которого исчерпаны, или потребителя (и соответствующий ему столбец), запросы которого полностью удовлетворены;
3) из оставшихся клеток снова выбираем клетку с наименьшим тарифом и записываем в нее максимально возможное значение поставки и т. д.
Как только весь груз распределен, получаем опорный план, который должен содержать  загруженных клеток.
загруженных клеток.
 загруженных клеток.
загруженных клеток.Метод потенциалов
Введем числа 
 и
и 
 которые будем называть потенциалами поставщиков и потребителей соответственно.
которые будем называть потенциалами поставщиков и потребителей соответственно.

 и
и 
 которые будем называть потенциалами поставщиков и потребителей соответственно.
которые будем называть потенциалами поставщиков и потребителей соответственно. Сумма потенциалов загруженной клетки  равна ее тарифу:
равна ее тарифу:
 (12.38)
(12.38)
 равна ее тарифу:
равна ее тарифу:  (12.38)
(12.38)Критерий оптимальности опорного плана: если все оценки свободных клеток неотрицательные, то план оптимальный.
Чтобы найти оценку свободной клетки  необходимо из тарифа клетки вычесть сумму ее потенциалов:
необходимо из тарифа клетки вычесть сумму ее потенциалов:
 (12.39)
(12.39)
 необходимо из тарифа клетки вычесть сумму ее потенциалов:
необходимо из тарифа клетки вычесть сумму ее потенциалов:  (12.39)
(12.39)Если среди оценок окажутся отрицательные, то клетку, которой соответствует наименьшая отрицательная оценка, называют перспективной.
План перевозок можно улучшить, перераспределяя максимально возможное количество груза по циклу, который образует перспективная клетка с другими загруженными клетками. Пример перераспределения груза приведен на рисунке 12.6.
Решение ТЗ удобно представлять в распределительной таблице:
Пример 1. Решите транспортную задачу (в таблице указаны тарифы перевозок):








Решение. Имеем закрытую модель задачи 12.35.
По правилу минимального элемента заполняем распределительную таблицу 12.1.
Наименьшие затраты на перевозку ( ден. ед.) соответствуют маршруту
ден. ед.) соответствуют маршруту  поэтому
поэтому  следовательно,
следовательно, 
 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны.
 ден. ед.) соответствуют маршруту
ден. ед.) соответствуют маршруту  поэтому
поэтому  следовательно,
следовательно, 
 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны. Из оставшихся тарифов наименьший ( ден. ед.) соответствует маршруту
ден. ед.) соответствует маршруту  поэтому
поэтому  следовательно,
следовательно, 

 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны.
 ден. ед.) соответствует маршруту
ден. ед.) соответствует маршруту  поэтому
поэтому  следовательно,
следовательно, 

 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны. Следующим рассматриваем маршрут  Тогда
Тогда  а
а 
 Тогда
Тогда  а
а 
Таблица 12.1
Опорный план должен содержать  загруженных клеток. Так как полученный план содержит
загруженных клеток. Так как полученный план содержит  загруженные клетки (одновременно исключались первая строка и второй столбец), в одну их свободных клеток запишем число
загруженные клетки (одновременно исключались первая строка и второй столбец), в одну их свободных клеток запишем число  и эту клетку будем считать условно загруженной. Например, пусть
и эту клетку будем считать условно загруженной. Например, пусть  (таблица 12.2).
(таблица 12.2).
 загруженных клеток. Так как полученный план содержит
загруженных клеток. Так как полученный план содержит  загруженные клетки (одновременно исключались первая строка и второй столбец), в одну их свободных клеток запишем число
загруженные клетки (одновременно исключались первая строка и второй столбец), в одну их свободных клеток запишем число  и эту клетку будем считать условно загруженной. Например, пусть
и эту клетку будем считать условно загруженной. Например, пусть  (таблица 12.2).
(таблица 12.2).Заполним таблицу 12.2. Найдем потенциалы поставщиков и потребителей.
Таблица 12.2
Так как среди оценок свободных отсутствуют отрицательные, то полученный план перевозок оптимальный.
План перевозок: 

Стоимость перевозок:
 (ден. ед.).
(ден. ед.).
 (ден. ед.).
(ден. ед.).Ответ:  ден. ед.,
ден. ед., 
 ден. ед.,
ден. ед., 
Пример 2. Требуется перевезти овощи из трех складов  запас которых соответственно равен
запас которых соответственно равен  и
и 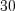 т, четырем заводам
т, четырем заводам  спрос которых равен соответственно
спрос которых равен соответственно  и
и  т. Известна матрица транспортных расходов на доставку
т. Известна матрица транспортных расходов на доставку  т овощей от поставщиков к потребителям:
т овощей от поставщиков к потребителям: ![\left [ c_{ij} \right ]=\begin{bmatrix} 6 & 5 & 4 & 3\\ 6 & 2& 8 & 7\\ 5 & 5 & 6& 3 \end{bmatrix} LaTeX formula: \left [ c_{ij} \right ]=\begin{bmatrix} 6 & 5 & 4 & 3\\ 6 & 2& 8 & 7\\ 5 & 5 & 6& 3 \end{bmatrix}](/uploads/formulas/a162296c14c31fc572fc155a1d5aeaa300688893.1.1.png) .
.
 запас которых соответственно равен
запас которых соответственно равен  и
и 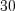 т, четырем заводам
т, четырем заводам  спрос которых равен соответственно
спрос которых равен соответственно  и
и  т. Известна матрица транспортных расходов на доставку
т. Известна матрица транспортных расходов на доставку  т овощей от поставщиков к потребителям:
т овощей от поставщиков к потребителям: ![\left [ c_{ij} \right ]=\begin{bmatrix} 6 & 5 & 4 & 3\\ 6 & 2& 8 & 7\\ 5 & 5 & 6& 3 \end{bmatrix} LaTeX formula: \left [ c_{ij} \right ]=\begin{bmatrix} 6 & 5 & 4 & 3\\ 6 & 2& 8 & 7\\ 5 & 5 & 6& 3 \end{bmatrix}](/uploads/formulas/a162296c14c31fc572fc155a1d5aeaa300688893.1.1.png) .
. Определите оптимальный план перевозок, минимизирующий суммарные транспортные расходы.
Решение. Найдем суммарный запас овощей: 

Найдем суммарный спрос на овощи:  .
.
 .
. Так как спрос превышает запас, то имеем открытую модель ТЗ и поэтому вводим фиктивного поставщика  полагая, что у него имеется в запасе
полагая, что у него имеется в запасе  т овощей.
т овощей.
 полагая, что у него имеется в запасе
полагая, что у него имеется в запасе  т овощей.
т овощей. По правилу минимального элемента заполняем распределительную таблицу 12.3.
Наименьшие затраты на перевозку ( ден. ед.) соответствуют маршруту
ден. ед.) соответствуют маршруту  поэтому
поэтому  следовательно,
следовательно, 

 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны.
 ден. ед.) соответствуют маршруту
ден. ед.) соответствуют маршруту  поэтому
поэтому  следовательно,
следовательно, 

 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны. Из оставшихся тарифов наименьший ( ден. ед.) соответствует маршрутам
ден. ед.) соответствует маршрутам  и
и  Если выберем первый маршрут, то
Если выберем первый маршрут, то  следовательно,
следовательно, 


 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны.
 ден. ед.) соответствует маршрутам
ден. ед.) соответствует маршрутам  и
и  Если выберем первый маршрут, то
Если выберем первый маршрут, то  следовательно,
следовательно, 


 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны. Следующим рассматриваем маршрут  Тогда
Тогда  следовательно,
следовательно, 
 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны.
 Тогда
Тогда  следовательно,
следовательно, 
 а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны. Далее выбираем маршрут  Тогда
Тогда  следовательно,
следовательно,  а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны.
 Тогда
Тогда  следовательно,
следовательно,  а соответствующие клетки таблицы свободны.
а соответствующие клетки таблицы свободны. Далее выбираем маршрут  Тогда
Тогда  следовательно,
следовательно,  а соответствующая клетка свободна.
а соответствующая клетка свободна.
 Тогда
Тогда  следовательно,
следовательно,  а соответствующая клетка свободна.
а соответствующая клетка свободна. Далее выбираем маршрут  Тогда
Тогда 
 Тогда
Тогда 
Таблица 12.3
Заполним таблицу 12.4. Найдем потенциалы поставщиков и потребителей.
Таблица 12.4
Поскольку имеем две отрицательные оценки, то опорный план задачи не оптимальный.
Клетку с оценкой  считаем перспективной. Она образует цикл с клетками
считаем перспективной. Она образует цикл с клетками  и
и  Перемещая по циклу
Перемещая по циклу  т груза, получим новый план перевозок, представленный в таблице 12.5.
т груза, получим новый план перевозок, представленный в таблице 12.5.
 считаем перспективной. Она образует цикл с клетками
считаем перспективной. Она образует цикл с клетками  и
и  Перемещая по циклу
Перемещая по циклу  т груза, получим новый план перевозок, представленный в таблице 12.5.
т груза, получим новый план перевозок, представленный в таблице 12.5. Таблица 12.5
Выполняя аналогичные преобразования, заполним таблицы 12.6 – 12.8.
Таблица 12.6
Таблица 12.7
Таблица 12.8
План перевозок: 

При этом потребитель  не получит
не получит  т овощей.
т овощей.
 не получит
не получит  т овощей.
т овощей.Стоимость перевозок:
 (ден. ед.).
(ден. ед.).
 (ден. ед.).
(ден. ед.).Ответ:  ден. ед.,
ден. ед., 
 ден. ед.,
ден. ед., 
1. В случае, когда из распределительной таблицы одновременно исключается строка и столбец, задача считается вырожденной. Тогда в свободные клетки записывают число  и такие клетки условно считают загруженными (нуль-загрузка).
и такие клетки условно считают загруженными (нуль-загрузка).
 и такие клетки условно считают загруженными (нуль-загрузка).
и такие клетки условно считают загруженными (нуль-загрузка).2. Все тарифы перевозок от поставщиков к фиктивному потребителю равны нулю. Все тарифы перевозок от фиктивного поставщика к потребителям также равны нулю.






 ,
,















