Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
























Рассмотрим взаимосвязь двух переменных  и
и  , в которой выделим одну из переменных как независимую (объясняющую), а другую как зависимую (объясняемую).
, в которой выделим одну из переменных как независимую (объясняющую), а другую как зависимую (объясняемую).
Изменение первой переменной может служить причиной изменения второй. Однако каждому конкретному значению объясняющей переменной может соответствовать не одно, а множество значений объясняемых переменных
может соответствовать не одно, а множество значений объясняемых переменных  . Поэтому анализируют, как объясняющая переменная влияет на зависимую переменную в среднем.
. Поэтому анализируют, как объясняющая переменная влияет на зависимую переменную в среднем.
Зависимость такого вида выражается соотношением и называется функцией регрессии
и называется функцией регрессии  на
на  .
.
 и
и  , в которой выделим одну из переменных как независимую (объясняющую), а другую как зависимую (объясняемую).
, в которой выделим одну из переменных как независимую (объясняющую), а другую как зависимую (объясняемую). Изменение первой переменной может служить причиной изменения второй. Однако каждому конкретному значению объясняющей переменной
 может соответствовать не одно, а множество значений объясняемых переменных
может соответствовать не одно, а множество значений объясняемых переменных  . Поэтому анализируют, как объясняющая переменная влияет на зависимую переменную в среднем.
. Поэтому анализируют, как объясняющая переменная влияет на зависимую переменную в среднем. Зависимость такого вида выражается соотношением
 и называется функцией регрессии
и называется функцией регрессии  на
на  .
.Пусть имеем следующие результаты измерений:
Вид зависимости между переменными величинами можно установить различными способами, например, графически, построив корреляционное поле, которое представляет собою множество построенных на координатной плоскости точек вида  , где
, где 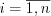 .
.
 , где
, где 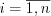 .
.Если все построенные точки незначительно уклоняются от некоторой прямой, то полагают, что между величинами  и
и  существует линейная зависимость (рис. 11.4).
существует линейная зависимость (рис. 11.4).
 и
и  существует линейная зависимость (рис. 11.4).
существует линейная зависимость (рис. 11.4).
Эмпирическое уравнение линейной регрессии  на
на  имеет вид:
имеет вид:


 на
на  имеет вид:
имеет вид: 

Эмпирические коэффициенты  и
и  находят, решая систему уравнений:
находят, решая систему уравнений:
 и
и  находят, решая систему уравнений:
находят, решая систему уравнений: 

Параметры эмпирических формул определяются по методу наименьших квадратов (МНК), т. е. минимизируется функция (рис. 11.5):


Если все построенные точки незначительно уклоняются от дуги некоторой параболы, то полагают, что между величинами  и
и  существует квадратичная зависимость (рис. 11.6).
существует квадратичная зависимость (рис. 11.6).
 и
и  существует квадратичная зависимость (рис. 11.6).
существует квадратичная зависимость (рис. 11.6).
Эмпирическое уравнение квадратичной регрессии  на
на  имеет вид:
имеет вид:
 на
на  имеет вид:
имеет вид:

Эмпирические коэффициенты  и
и  находят, решая систему уравнений:
находят, решая систему уравнений:
 и
и  находят, решая систему уравнений:
находят, решая систему уравнений: 

Пример. Проанализировано 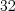 слова из фрагмента произведения С. Есенина:
слова из фрагмента произведения С. Есенина:  – количество бука в слове;
– количество бука в слове;  – количество согласных в слове.
– количество согласных в слове.
Получены следующие значения двумерной случайной величины



Необходимо: 1) построить корреляционное поле; 2) найти и построить уравнение регрессии.
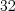 слова из фрагмента произведения С. Есенина:
слова из фрагмента произведения С. Есенина:  – количество бука в слове;
– количество бука в слове;  – количество согласных в слове.
– количество согласных в слове. Получены следующие значения двумерной случайной величины




Необходимо: 1) построить корреляционное поле; 2) найти и построить уравнение регрессии.
Решение. 1. Построим корреляционное поле (рис. 11. 7).


Вычитая из первого уравнения второе, получим:

Подставляя это значение в уравнение получим:
получим:


Подставляя это значение в уравнение
 получим:
получим: 
3. Построим прямую регрессии (рис. 11.8).

Если имеем две объясняющие переменные, то, используя МНК, коэффициенты эмпирического уравнения регрессии

рассчитывают по формулам:


Дисперсии и стандартные ошибки коэффициентов рассчитывают по формулам ( – объем выборки):
– объем выборки):
 – объем выборки):
– объем выборки): 





Статистическую значимость коэффициентов регрессии  и
и  устанавливают на основе
устанавливают на основе  -статистики:
-статистики:  и
и 
 и
и  устанавливают на основе
устанавливают на основе  -статистики:
-статистики:  и
и 
Проверяются гипотезы: 1)  2)
2) 
 2)
2) 
Если  и
и  (
(  – уровень значимости,
– уровень значимости,  – объем выборки), то данные коэффициенты статистически значимы.
– объем выборки), то данные коэффициенты статистически значимы.
 и
и  (
(  – уровень значимости,
– уровень значимости,  – объем выборки), то данные коэффициенты статистически значимы.
– объем выборки), то данные коэффициенты статистически значимы. Доверительные интервалы коэффициентов регрессии рассчитывают по формуле:

Коэффициент детерминации рассчитывают по формуле 

Статистическая значимость коэффициента детерминации проверяется с помощью гипотезы: 

С помощью статистики Фишера находят 

При уровне значимости  находят критическое значение распределения Фишера:
находят критическое значение распределения Фишера: 
 находят критическое значение распределения Фишера:
находят критическое значение распределения Фишера: 
Если 

 , то нулевая гипотеза отклоняется, следовательно, коэффициент детерминации статистически значим.
, то нулевая гипотеза отклоняется, следовательно, коэффициент детерминации статистически значим.


 , то нулевая гипотеза отклоняется, следовательно, коэффициент детерминации статистически значим.
, то нулевая гипотеза отклоняется, следовательно, коэффициент детерминации статистически значим.Гипотеза об отсутствии автокорреляции проверяется на основе статистики Дарбина – Уотсона  , которая определяется по формуле:
, которая определяется по формуле: 
 , которая определяется по формуле:
, которая определяется по формуле: 
Если выполняется условие , то автокорреляция остатков отсутствует.
, то автокорреляция остатков отсутствует.
 , то автокорреляция остатков отсутствует.
, то автокорреляция остатков отсутствует.






