Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
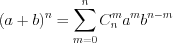 . (10.40)
. (10.40) , (10.41)
, (10.41)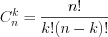 . (10.41.1)
. (10.41.1)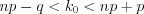 . (10.42)
. (10.42)
 , (10.43)
, (10.43)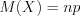 . (10.44)
. (10.44)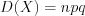 . (10.45)
. (10.45)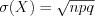 . (10.46)
. (10.46) , (10.47)
, (10.47)
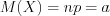 . (10.48)
. (10.48)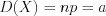 . (10.49)
. (10.49)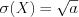 . (10.50)
. (10.50) . (10.51)
. (10.51)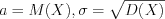 . (10.52)
. (10.52)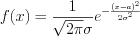 . (10.53)
. (10.53)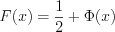 , (10.54)
, (10.54)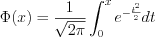 , (10.55)
, (10.55) , (10.58)
, (10.58)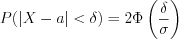 , (10.59)
, (10.59) . (10.60)
. (10.60)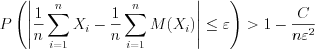 , (10.61)
, (10.61)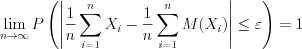 . (10.61.1)
. (10.61.1) , (10.61.2)
, (10.61.2)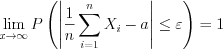 . (10.61.3)
. (10.61.3)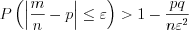 , (10.62)
, (10.62)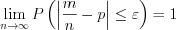 . (10.62.1)
. (10.62.1)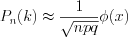 , (10.63)
, (10.63)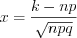 , (10.63.1)
, (10.63.1) . (10.63.2)
. (10.63.2)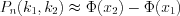 , (10.64)
, (10.64) , (10.64.1)
, (10.64.1)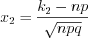 , (10.64.2)
, (10.64.2)
 .
.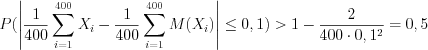 .
.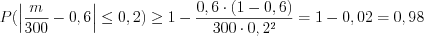 .
.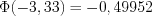 ,
, 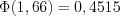 .
.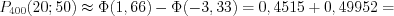
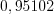 .
.
Биномиальное распределение
Биномом Ньютона называют выражение вида
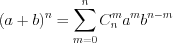 . (10.40)
. (10.40)Формула 10.40 имеет непосредственное отношение к закону распределения  , который называют биномиальным.
, который называют биномиальным.
 , который называют биномиальным.
, который называют биномиальным.Рассмотрим  испытаний, в каждом из которых может появиться с одной и той же вероятностью
испытаний, в каждом из которых может появиться с одной и той же вероятностью  событие
событие  или cобытие
или cобытие 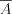 с вероятностью
с вероятностью 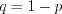 .
.
Пусть случайная величина – число появлений события
– число появлений события  . В таком случае она может принимать следующие значения:
. В таком случае она может принимать следующие значения:
 (событие не появится ни разу),
(событие не появится ни разу), 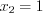 (событие появится один раз),
(событие появится один раз), 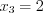 , …,
, …,  (появится во всех испытаниях).
(появится во всех испытаниях).
 испытаний, в каждом из которых может появиться с одной и той же вероятностью
испытаний, в каждом из которых может появиться с одной и той же вероятностью  событие
событие  или cобытие
или cобытие 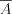 с вероятностью
с вероятностью 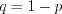 .
. Пусть случайная величина
 – число появлений события
– число появлений события  . В таком случае она может принимать следующие значения:
. В таком случае она может принимать следующие значения: (событие не появится ни разу),
(событие не появится ни разу), 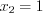 (событие появится один раз),
(событие появится один раз), 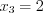 , …,
, …,  (появится во всех испытаниях).
(появится во всех испытаниях). Вероятность того, что в серии из  независимых испытаний событие
независимых испытаний событие  появится ровно
появится ровно  раз (биномиальную вероятность) можно найти по формуле Бернулли:
раз (биномиальную вероятность) можно найти по формуле Бернулли:
 независимых испытаний событие
независимых испытаний событие  появится ровно
появится ровно  раз (биномиальную вероятность) можно найти по формуле Бернулли:
раз (биномиальную вероятность) можно найти по формуле Бернулли:  , (10.41)
, (10.41)где
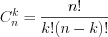 . (10.41.1)
. (10.41.1)Наивероятнейшим числом появления события  называют такое число
называют такое число 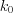 , которому соответствует наибольшая биномиальная вероятность
, которому соответствует наибольшая биномиальная вероятность 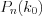 .
.
 называют такое число
называют такое число 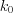 , которому соответствует наибольшая биномиальная вероятность
, которому соответствует наибольшая биномиальная вероятность 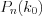 .
. Наивероятнейшее число 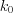 находят их системы неравенств:
находят их системы неравенств:
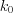 находят их системы неравенств:
находят их системы неравенств: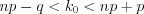 . (10.42)
. (10.42)Числа  и
и  называют параметрами биномиального распределения
называют параметрами биномиального распределения  .
.
 и
и  называют параметрами биномиального распределения
называют параметрами биномиального распределения  .
. Биномиальный закон может быть представлен в таблице:

Сумма всех биномиальных вероятностей равна единице:
 , (10.43)
, (10.43)Числовые характеристики 

1. Математическое ожидание  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле: 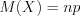 . (10.44)
. (10.44)2. Дисперсию  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле: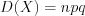 . (10.45)
. (10.45)3. Среднеквадратическое отклонение находят по формуле:
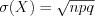 . (10.46)
. (10.46)Распределение Пуассона
Рассмотрим  испытаний, в каждом из которых может появиться с одной и той же вероятностью
испытаний, в каждом из которых может появиться с одной и той же вероятностью  событие
событие  .
.
Пусть случайная величина – число появлений события
– число появлений события  . Вероятность того, что в серии из
. Вероятность того, что в серии из  независимых испытаний событие
независимых испытаний событие  появится ровно
появится ровно  раз (биномиальную вероятность) можно найти по формуле Бернулли 10.41.
раз (биномиальную вероятность) можно найти по формуле Бернулли 10.41.
В случае, если число достаточное большое, а
достаточное большое, а  достаточно мало, то имеем распределение Пуассона, а вероятность того, что в серии из
достаточно мало, то имеем распределение Пуассона, а вероятность того, что в серии из  независимых испытаний событие
независимых испытаний событие  появится ровно
появится ровно  раз можно найти по формуле:
раз можно найти по формуле:
 испытаний, в каждом из которых может появиться с одной и той же вероятностью
испытаний, в каждом из которых может появиться с одной и той же вероятностью  событие
событие  .
. Пусть случайная величина
 – число появлений события
– число появлений события  . Вероятность того, что в серии из
. Вероятность того, что в серии из  независимых испытаний событие
независимых испытаний событие  появится ровно
появится ровно  раз (биномиальную вероятность) можно найти по формуле Бернулли 10.41.
раз (биномиальную вероятность) можно найти по формуле Бернулли 10.41. В случае, если число
 достаточное большое, а
достаточное большое, а  достаточно мало, то имеем распределение Пуассона, а вероятность того, что в серии из
достаточно мало, то имеем распределение Пуассона, а вероятность того, что в серии из  независимых испытаний событие
независимых испытаний событие  появится ровно
появится ровно  раз можно найти по формуле:
раз можно найти по формуле:  , (10.47)
, (10.47)где 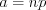 – параметр распределения.
– параметр распределения.
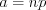 – параметр распределения.
– параметр распределения. Закон распределения Пуассона может быть представлен в таблице:

Числовые характеристики 

1. Математическое ожидание  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле: 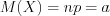 . (10.48)
. (10.48)2. Дисперсию  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле: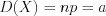 . (10.49)
. (10.49)3. Среднеквадратическое отклонение находят по формуле:
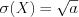 . (10.50)
. (10.50)Нормальное распределение
Случайная величина  распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами  и
и  , если ее функция распределения имеет вид:
, если ее функция распределения имеет вид:
 распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами  и
и  , если ее функция распределения имеет вид:
, если ее функция распределения имеет вид: . (10.51)
. (10.51)Записывают: 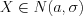 , причем
, причем
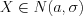 , причем
, причем 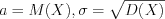 . (10.52)
. (10.52)График плотности нормального распределения называют нормальной кривой Гаусса, уравнение которой имеет вид:
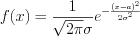 . (10.53)
. (10.53)Если  и
и 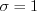 , то
, то
 и
и 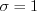 , то
, то 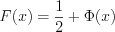 , (10.54)
, (10.54)где 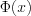 – функция Лапласа:
– функция Лапласа:
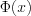 – функция Лапласа:
– функция Лапласа: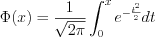 , (10.55)
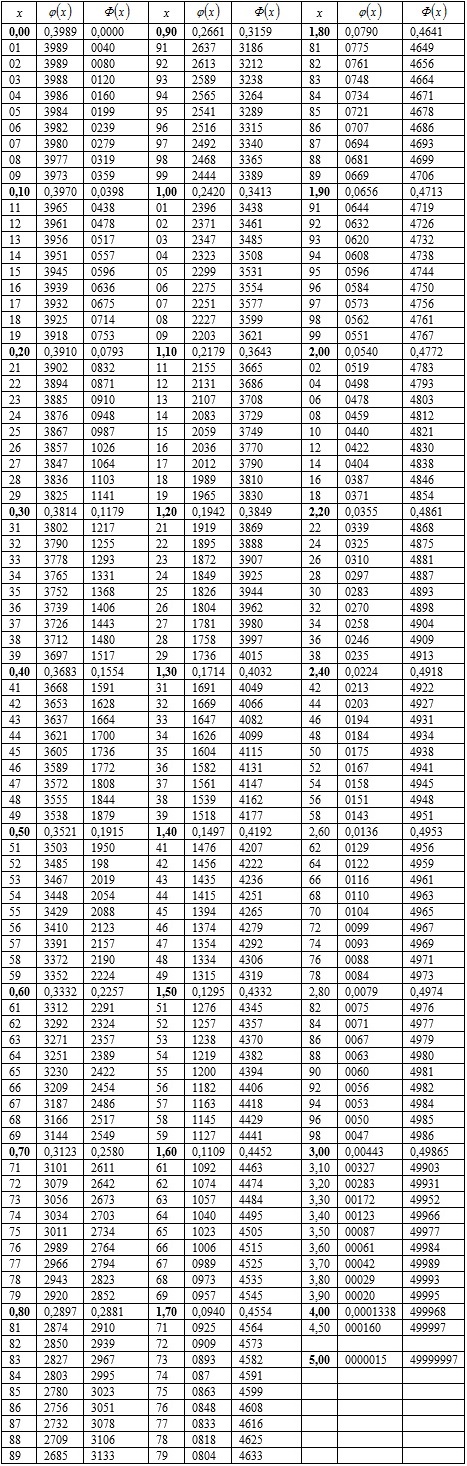
, (10.55)значения которой приведены в таблице приложения II.
Свойства функции Лапласа 10.55
1. 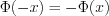 . (10.56)
. (10.56)
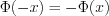 . (10.56)
. (10.56)2. 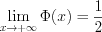 . (10.57)
. (10.57)
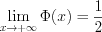 . (10.57)
. (10.57)Вероятность попадания нормально распределенной случайной величины  в заданный интервал находят по формуле:
в заданный интервал находят по формуле:
 в заданный интервал находят по формуле:
в заданный интервал находят по формуле:  , (10.58)
, (10.58)Вероятность отклонения случайной величины  от математического ожидания на величину не превышающую
от математического ожидания на величину не превышающую  находят по формуле:
находят по формуле:
 от математического ожидания на величину не превышающую
от математического ожидания на величину не превышающую  находят по формуле:
находят по формуле: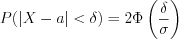 , (10.59)
, (10.59)Правило трех сигм: если  распределена нормально, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения:
распределена нормально, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения:
 распределена нормально, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения:
распределена нормально, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения:  . (10.60)
. (10.60)Это означает, что событие, состоящее в осуществлении неравенства 10.60, имеет вероятность, близкую к единице, т. е. является почти достоверным.
Предельные теоремы
Теорема Чебышева
Если случайные величины 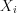 , где
, где 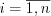 , независимы, имеют математические ожидания
, независимы, имеют математические ожидания 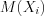 и дисперсии
и дисперсии 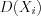 , ограниченные одним и тем же числом
, ограниченные одним и тем же числом  , то для любого числа
, то для любого числа 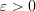 выполняется неравенство
выполняется неравенство
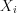 , где
, где 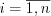 , независимы, имеют математические ожидания
, независимы, имеют математические ожидания 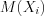 и дисперсии
и дисперсии 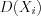 , ограниченные одним и тем же числом
, ограниченные одним и тем же числом  , то для любого числа
, то для любого числа 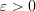 выполняется неравенство
выполняется неравенство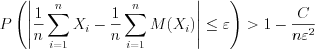 , (10.61)
, (10.61)откуда следует, что
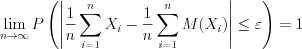 . (10.61.1)
. (10.61.1)Если все случайные величины 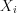 , где
, где 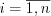 , имеют одно и то же математические ожидания
, имеют одно и то же математические ожидания 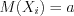 , то неравенство 10.61 примет вид
, то неравенство 10.61 примет вид
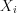 , где
, где 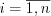 , имеют одно и то же математические ожидания
, имеют одно и то же математические ожидания 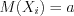 , то неравенство 10.61 примет вид
, то неравенство 10.61 примет вид , (10.61.2)
, (10.61.2)откуда следует, что
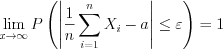 . (10.61.3)
. (10.61.3)Теорема Бернулли
Если вероятность  появления события
появления события  в каждом из
в каждом из  независимых испытаний постоянна, то вероятность того, что отклонение частоты
независимых испытаний постоянна, то вероятность того, что отклонение частоты  от вероятности
от вероятности  по модулю не превзойдет числа
по модулю не превзойдет числа 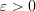 , больше, чем на
, больше, чем на  :
:
 появления события
появления события  в каждом из
в каждом из  независимых испытаний постоянна, то вероятность того, что отклонение частоты
независимых испытаний постоянна, то вероятность того, что отклонение частоты  от вероятности
от вероятности  по модулю не превзойдет числа
по модулю не превзойдет числа 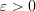 , больше, чем на
, больше, чем на  :
: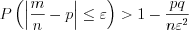 , (10.62)
, (10.62)откуда следует, что
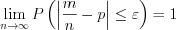 . (10.62.1)
. (10.62.1)Локальная теорема Лапласа
Если вероятность  появления события
появления события  в каждом из
в каждом из  независимых испытаний постоянна, то вероятность
независимых испытаний постоянна, то вероятность 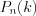 того, что во всех этих испытаниях событие
того, что во всех этих испытаниях событие  появится ровно
появится ровно  раз, приближенно выражается формулой:
раз, приближенно выражается формулой:
 появления события
появления события  в каждом из
в каждом из  независимых испытаний постоянна, то вероятность
независимых испытаний постоянна, то вероятность 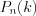 того, что во всех этих испытаниях событие
того, что во всех этих испытаниях событие  появится ровно
появится ровно  раз, приближенно выражается формулой:
раз, приближенно выражается формулой: 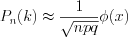 , (10.63)
, (10.63)при
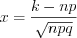 , (10.63.1)
, (10.63.1)где
 . (10.63.2)
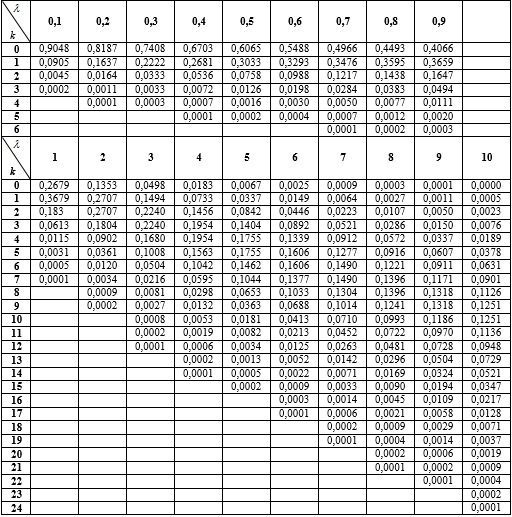
. (10.63.2)Значения малой функции Лапласа 10.63.2 находят по таблице П1, приведенной во вкладке Обратите внимание.
Интегральная теорема Лапласа
Если вероятность  появления события
появления события  в каждом из
в каждом из  независимых испытаний постоянна, то вероятность
независимых испытаний постоянна, то вероятность 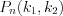 того, что во всех этих испытаниях событие
того, что во всех этих испытаниях событие  появится не менее
появится не менее 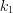 раз и не более
раз и не более 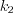 раз, приближенно выражается формулой:
раз, приближенно выражается формулой:
 появления события
появления события  в каждом из
в каждом из  независимых испытаний постоянна, то вероятность
независимых испытаний постоянна, то вероятность 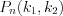 того, что во всех этих испытаниях событие
того, что во всех этих испытаниях событие  появится не менее
появится не менее 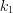 раз и не более
раз и не более 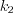 раз, приближенно выражается формулой:
раз, приближенно выражается формулой: 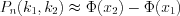 , (10.64)
, (10.64)при
 , (10.64.1)
, (10.64.1)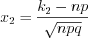 , (10.64.2)
, (10.64.2)Пример 1. Вероятность выпадения осадков в каждый из первых пяти дней сентября равна  . Найдите вероятность того, что осадки будут выпадать:
. Найдите вероятность того, что осадки будут выпадать:
1) дней; 2) менее двух дней.
дней; 2) менее двух дней.
 . Найдите вероятность того, что осадки будут выпадать:
. Найдите вероятность того, что осадки будут выпадать: 1)
 дней; 2) менее двух дней.
дней; 2) менее двух дней. 1) 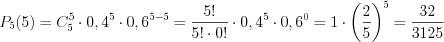 ;
;
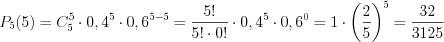 ;
;2)  ,
,
 ,
,
 ,
,  ,
,  .
.Ответ:  ,
, 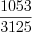 .
.
 ,
, 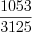 .
. Пример 2. Вероятность изготовления бракованной детали равна  %. Найдите среднее количество бракованных деталей в партии из
%. Найдите среднее количество бракованных деталей в партии из 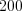 деталей.
деталей.
 %. Найдите среднее количество бракованных деталей в партии из
%. Найдите среднее количество бракованных деталей в партии из 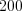 деталей.
деталей. Пример 3. Вероятность изготовления бракованной детали равна  %. Найдите наивероятнейшее число стандартных деталей в партии из
%. Найдите наивероятнейшее число стандартных деталей в партии из 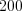 деталей.
деталей.
 %. Найдите наивероятнейшее число стандартных деталей в партии из
%. Найдите наивероятнейшее число стандартных деталей в партии из 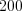 деталей.
деталей. Пример 4. Изготовлено  стеклянных шаров. Вероятность разбить шар при его упаковке равна
стеклянных шаров. Вероятность разбить шар при его упаковке равна 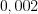 . Найдите вероятность того, что будет разбито
. Найдите вероятность того, что будет разбито  шаров.
шаров.
 стеклянных шаров. Вероятность разбить шар при его упаковке равна
стеклянных шаров. Вероятность разбить шар при его упаковке равна 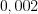 . Найдите вероятность того, что будет разбито
. Найдите вероятность того, что будет разбито  шаров.
шаров.Решение. Согласно условию задачи 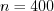 ,
, 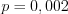 ,
, 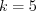 .
.
По формуле 10.48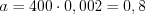 .
.
По формуле 10.47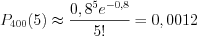 .
.
Значения функции 10.63.2 приведены во вкладке «Обратите внимание!».
Ответ: .
.
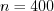 ,
, 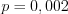 ,
, 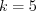 .
. По формуле 10.48
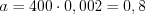 .
. По формуле 10.47
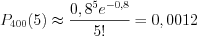 .
. Значения функции 10.63.2 приведены во вкладке «Обратите внимание!».
Ответ:
 .
.Пример 5. Количество нерешенных тестовых заданий имеет нормальное распределение с параметры  и
и 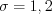 . Найдите вероятность того, что тестируемый не решит от двух до пяти задач.
. Найдите вероятность того, что тестируемый не решит от двух до пяти задач.
 и
и 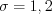 . Найдите вероятность того, что тестируемый не решит от двух до пяти задач.
. Найдите вероятность того, что тестируемый не решит от двух до пяти задач. Решение. Согласно формуле 10.58 получим:
 ,
,
 ,
,
 .
.
Значения функции 10.55 найдены по таблице П2 во вкладке «Обратите внимание».
Ответ: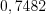 .
.
 ,
, ,
,  .
. Значения функции 10.55 найдены по таблице П2 во вкладке «Обратите внимание».
Ответ:
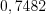 .
.Пример 6. Нормальное распределение  имеет параметры
имеет параметры  ,
,  . Найдите вероятность отклонения
. Найдите вероятность отклонения  от ее среднего значения на величину, не превышающую
от ее среднего значения на величину, не превышающую 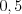 .
.
 имеет параметры
имеет параметры  ,
,  . Найдите вероятность отклонения
. Найдите вероятность отклонения  от ее среднего значения на величину, не превышающую
от ее среднего значения на величину, не превышающую 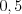 .
.Пример 7. Дисперсии каждой из  независимых
независимых  равны
равны  . Найдите вероятность того, что отклонение среднего арифметического значения
. Найдите вероятность того, что отклонение среднего арифметического значения  от среднего арифметического их математических ожиданий по модулю не превзойдет
от среднего арифметического их математических ожиданий по модулю не превзойдет 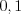 .
.
 независимых
независимых  равны
равны  . Найдите вероятность того, что отклонение среднего арифметического значения
. Найдите вероятность того, что отклонение среднего арифметического значения  от среднего арифметического их математических ожиданий по модулю не превзойдет
от среднего арифметического их математических ожиданий по модулю не превзойдет 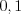 .
.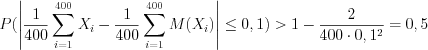 .
.Ответ: 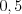 .
.
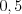 .
.Пример 8. Событие  может появиться с вероятностью
может появиться с вероятностью 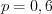 в каждом из
в каждом из 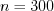 независимых испытаний. Найдите вероятность того, что отклонение частоты события от вероятности его появления по модулю не превзойдет
независимых испытаний. Найдите вероятность того, что отклонение частоты события от вероятности его появления по модулю не превзойдет 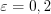 .
.
 может появиться с вероятностью
может появиться с вероятностью 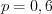 в каждом из
в каждом из 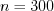 независимых испытаний. Найдите вероятность того, что отклонение частоты события от вероятности его появления по модулю не превзойдет
независимых испытаний. Найдите вероятность того, что отклонение частоты события от вероятности его появления по модулю не превзойдет 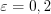 .
.Решение. Согласно формуле 10.62 запишем:
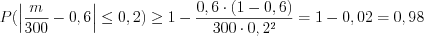 .
.Ответ:  .
.
 .
.Пример 9. Вероятность изготовления бракованного изделия равна 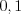 . Найдите вероятность того, что в партии из
. Найдите вероятность того, что в партии из  изделий окажется
изделий окажется 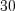 бракованных.
бракованных.
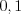 . Найдите вероятность того, что в партии из
. Найдите вероятность того, что в партии из  изделий окажется
изделий окажется 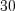 бракованных.
бракованных. Пример 10. Вероятность изготовления бракованного изделия равна 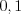 . Найдите вероятность того, что в партии из
. Найдите вероятность того, что в партии из  изделий окажется не менее
изделий окажется не менее 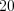 и не более
и не более  бракованных.
бракованных.
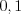 . Найдите вероятность того, что в партии из
. Найдите вероятность того, что в партии из  изделий окажется не менее
изделий окажется не менее 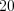 и не более
и не более  бракованных.
бракованных. Решение. Согласно условию задачи:
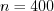 ,
, 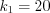 ,
, 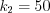 ,
, 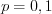 ,
, 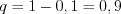 .
.
Тогда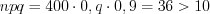 .
.
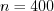 ,
, 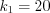 ,
, 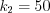 ,
, 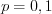 ,
, 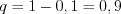 .
. Тогда
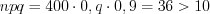 .
. 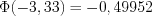 ,
, 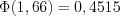 .
.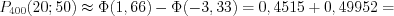
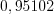 .
.Ответ: 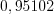 .
.
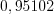 .
.

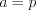 ,
, 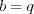
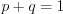 , формула
, формула 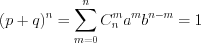
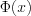 – функция Лапласа
– функция Лапласа 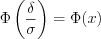 – функция Лапласа
– функция Лапласа 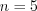 ,
, 
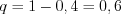 , то согласно формулам
, то согласно формулам  ,
, 
 .
. 
 ,
, 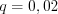
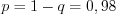 .
. 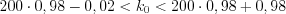
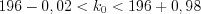

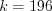 .
. 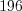
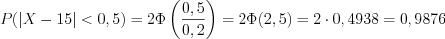

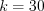
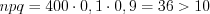 .
. 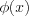
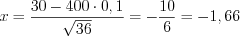
 .
. 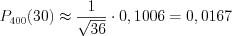 .
. 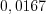
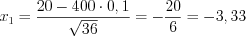

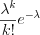 приведены в таблице П1.
приведены в таблице П1.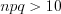 .
.