Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (10.15)
. (10.15) , (10.16)
, (10.16)
 ,
,  .
.  ,
,  ,
,  .
.  ,
,
 .
.  ,
,
 .
.
Рассмотрим событие  , которое может осуществляться с одним из попарно несовместных событий
, которое может осуществляться с одним из попарно несовместных событий  ,
,  , …,
, …,  .
.
Если известны вероятности ,
,  , …,
, …,  и условные вероятности
и условные вероятности  ,
,  , …,
, …,  , то вероятность события
, то вероятность события  можно найти по формуле:
можно найти по формуле:
 , которое может осуществляться с одним из попарно несовместных событий
, которое может осуществляться с одним из попарно несовместных событий  ,
,  , …,
, …,  .
. Если известны вероятности
 ,
,  , …,
, …,  и условные вероятности
и условные вероятности  ,
,  , …,
, …,  , то вероятность события
, то вероятность события  можно найти по формуле:
можно найти по формуле: . (10.15)
. (10.15)Формулы Байеса
Известно, что в результате некоторого опыта появилось событие  .
.
Условные вероятности находят по формуле:
находят по формуле:
 .
. Условные вероятности
 находят по формуле:
находят по формуле: , (10.16)
, (10.16)где  ,
,  - полная вероятность. события
- полная вероятность. события  .
.
 ,
,  - полная вероятность. события
- полная вероятность. события  .
. Пример. Рабочие производят однотипные детали. Первый рабочий за смену производит 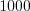 деталей, второй
деталей, второй  , а третий
, а третий  . Брак у первого рабочего составляет
. Брак у первого рабочего составляет  %, у второго –
%, у второго –  %, а у третьего –
%, а у третьего –  %. Взятая наудачу деталь оказалась бракованной. Какова вероятность того, что ее произвел третий рабочий?
%. Взятая наудачу деталь оказалась бракованной. Какова вероятность того, что ее произвел третий рабочий?
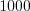 деталей, второй
деталей, второй  , а третий
, а третий  . Брак у первого рабочего составляет
. Брак у первого рабочего составляет  %, у второго –
%, у второго –  %, а у третьего –
%, а у третьего –  %. Взятая наудачу деталь оказалась бракованной. Какова вероятность того, что ее произвел третий рабочий?
%. Взятая наудачу деталь оказалась бракованной. Какова вероятность того, что ее произвел третий рабочий?Решение. Пусть  – событие, состоящее в том, что наудачу взятое изделие оказалось бракованным,
– событие, состоящее в том, что наудачу взятое изделие оказалось бракованным,  ,
,  и
и  – события, состоящие в том, что изделие произведено первым, вторым и третьим рабочим соответственно.
– события, состоящие в том, что изделие произведено первым, вторым и третьим рабочим соответственно.
Тогда:
 ,
,
 – событие, состоящее в том, что наудачу взятое изделие оказалось бракованным,
– событие, состоящее в том, что наудачу взятое изделие оказалось бракованным,  ,
,  и
и  – события, состоящие в том, что изделие произведено первым, вторым и третьим рабочим соответственно.
– события, состоящие в том, что изделие произведено первым, вторым и третьим рабочим соответственно. Тогда:
 ,
,  ,
,  .
. Согласно условию задачи:
 ,
,  ,
,  .
. По формуле полной вероятности 10.15 получим:
 ,
,  .
. По формуле Байеса 10.16:
 ,
,  .
.Ответ:  .
.
 .
.В формулах Байеса 10.16
события называют гипотезами,
называют гипотезами,
 – априорными вероятностями гипотез,
– априорными вероятностями гипотез,
 – апостериорными вероятностями гипотез.
– апостериорными вероятностями гипотез.
события
 называют гипотезами,
называют гипотезами,  – априорными вероятностями гипотез,
– априорными вероятностями гипотез,  – апостериорными вероятностями гипотез.
– апостериорными вероятностями гипотез.
