Многогранники
Многогранником называют пространственное тело, ограниченное плоскими многоугольниками. Многоугольники называют гранями многогранника, стороны многоугольников – ребрами многогранника, а вершины многоугольников – вершинами многогранника.
Стороны граней называют ребрами, а вершины граней – вершинами прямоугольного параллелепипеда.
Длины ребер называют измерениями прямоугольного параллелепипеда: длина, ширина и высота.
Противолежащие грани прямоугольного параллелепипеда равны.
2. Кубом называют прямоугольный параллелепипед с равными ребрами.
Все грани куба – квадраты (Рис. 2).
3. Пирамидой называют
многогранник, одна грань которого – многоугольник, а остальные грани –
треугольники с общей вершиной.
Многоугольник
называют основанием пирамиды, а треугольники – боковыми
гранями.
Общую
вершину боковых граней называют вершиной пирамиды.
Стороны
основания пирамиды называются ребрами основания пирамиды.
Стороны
боковых граней, не принадлежащие основанию, называют боковыми ребрами пирамиды.
Н а п р и м е р,
на Рисунке 3 изображена треугольная пирамида  с вершиной в
точке
с вершиной в
точке  . Треугольник
. Треугольник  – основание
пирамиды, треугольники
– основание
пирамиды, треугольники  ,
,  и
и  –
ее боковые грани. Отрезки
–
ее боковые грани. Отрезки  ,
,  и
и  –
боковые ребра пирамиды.
–
боковые ребра пирамиды.
Н а п р и м е р, на Рисунке 4 изображена четырехугольная
пирамида  с вершиной в
точке
с вершиной в
точке  и основанием
и основанием  .
.
Площади
Измерить площадь фигуры
– значит подсчитать, сколько единичных квадратов в ней помещается.
Единицы
измерения
площади: квадратный миллиметр (мм2), квадратный сантиметр (см2),
квадратный дециметр (дм2), квадратный метр (м2),
квадратный километр (км2), ар (а), гектар (га).
Меры площади:
1 см2 = 100 мм2;
1 дм2 = 100 см2;
1 м2 = 100 дм2;
1 а = 100 м2;
1 га = 100 а =
10 000 м2;
1 км2 = 1
0002 м2 = 1 000 000 м2.
Площадь прямоугольника находят по формуле:
 ,
,
где  и
и  – длины соседних (смежных) сторон прямоугольника, выраженные в одних и тех же единицах измерения.
– длины соседних (смежных) сторон прямоугольника, выраженные в одних и тех же единицах измерения.
Площадь квадрата находят по формуле:

(где  – длина стороны квадрата).
– длина стороны квадрата).
Объемы
Измерить объем фигуры – значит подсчитать, сколько единичных
кубов в ней помещается.
Единицы измерения объема: кубический миллиметр (мм3),
кубический сантиметр (см3), кубический дециметр (дм3), кубический
метр (м3), литр (л).
Меры объема:
1 см3 = 1 000 мм3;
1 дм3 = 1 000 см3;
1 м3 = 1 000 дм3;
1 л = 1 дм3.
Объем прямоугольного параллелепипеда равен
произведению трех его измерений:
 ,
,
где  – длина,
– длина,  – ширина,
– ширина,  – высота, выраженные в одних и тех же
единицах измерения.
– высота, выраженные в одних и тех же
единицах измерения.
Объем прямоугольного
параллелепипеда можно вычислить и по формуле:
 ,
,
где  – площадь основания,
– площадь основания,  – высота.
– высота.
Объем куба находят по формуле:
 ,
,
где  – длина ребра куба.
– длина ребра куба.
Пример 1. Квадрат со стороной  см и прямоугольник,
длина которого равна
см и прямоугольник,
длина которого равна  см, имеют равные площади. Найдите периметр прямоугольника.
см, имеют равные площади. Найдите периметр прямоугольника.
Решение.
1. Зная сторону
квадрата, найдем его площадь:
 (см2).
(см2).
2. Зная площадь
прямоугольника  см2 и
его длину
см2 и
его длину  см, найдем ширину (площадь разделим на
длину:
см, найдем ширину (площадь разделим на
длину:
 (см).
(см).
3. Найдем периметр прямоугольника
(сумму длин всех его сторон):
 (см).
(см).
Ответ: периметр прямоугольника равен  см.
см.
Пример 2. Ванна, имеющая форму прямоугольного
параллелепипеда, вмещает  литров воды, а площадь ее дна равна
литров воды, а площадь ее дна равна  дм2.
Найдите высоту ванны.
дм2.
Найдите высоту ванны.
Решение.
Так как  л =
л =  дм3,
то
дм3,
то  л =
л =  дм3. Следовательно, объем параллелепипеда равен
дм3. Следовательно, объем параллелепипеда равен  дм3.
дм3.
Из формулы объема  следует, что
следует, что  .
.
Найдем высоту ванны:  (дм).
(дм).
Ответ: высота ванны равна  дм.
дм.
Пример 3. Площадь поверхности куба равна 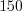 см2.
Найдите объем куба.
см2.
Найдите объем куба.
Решение.
Так как поверхность
куба состоит из  граней, то площадь одной грани (одного квадрата) равна:
граней, то площадь одной грани (одного квадрата) равна:
 (см2).
(см2).
Так как  см2,
то сторона квадрата (длина ребра куба) равна
см2,
то сторона квадрата (длина ребра куба) равна  см.
см.
Найдем объем куба:
 ,
,  (см3).
(см3).
Ответ: объем куба равен  см3.
см3.
1. Равные фигуры имеют
одинаковые площади. Площадь фигуры равна сумме площадей фигур, из которых она
состоит.
2. Равные фигуры имеют
одинаковые объемы. Объем фигуры равен сумме объемов фигур, из которых она
состоит.
3. Если в задании
присутствуют разные единицы измерения, то перед выполнением действий необходимо
перевести их в одни и те же (наиболее удобные для счета).

