Углы

Углом называют фигуру, образованную двумя лучами, исходящими из одной точки (вершины угла) (Рис. 1).
Н а п р и м е р, на Рисунке 1 точка  – вершина угла, лучи  и  – стороны угла.

Угол можно обозначать тремя прописными буквами так, чтобы буква, обозначающая вершину угла, стояла между двумя другими буквами или одной прописной буквой, обозначающей вершину угла.
Н а п р и м е р, на Рисунке 1 изображен угол  (или угол ).

Биссектрисой угла называют луч, который выходит из вершины угла и делит этот угол на два равных угла.

Н а п р и м е р, на Рисунке 2 луч  – биссектриса угла , так как углы  и  равны. 

 Развернутым называют угол, стороны которого являются дополнительными полупрямыми одной прямой (Рис. 3). 
Основной единицей измерения углов считают угол в  градус. 
Развернутый угол равен .

 Виды углов

1. Острым углом называют угол, градусная мера которого меньше  (Рис. 4).

2. Тупым углом называют угол, градусная мера которого больше , но меньше  (Рис. 5).

3. Прямым углом называют угол, градусная мера которого равна  (Рис. 6).

Многоугольники

Многоугольником на плоскости называют фигуру, состоящую из точек и соединяющих их непересекающихся отрезков. Точки называют вершинами многоугольника, а отрезки – сторонами.
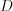Н а п р и м е р, на Рисунке 7 изображен пятиугольник . Точки , , ,  и  – его вершины, а отрезки , , ,  и  – стороны.

Две вершины многоугольника называются смежными, если они соединяются стороной многоугольника.
Две стороны многоугольника называются смежными, если они имеют общую вершину.
Н а п р и м е р, на Рисунке 7 вершины  и  – смежные, стороны  и  – смежные.
Периметром многоугольника называют сумму длин всех его сторон.

Четырехугольники

Четырехугольником называют многоугольник, имеющий четыре вершины.

1. Прямоугольником называют четырехугольник, все углы которого прямые (Рис. 8).
Свойство прямоугольника: противоположные стороны прямоугольника равны. 
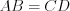Н а п р и м е р, в прямоугольнике  (Рис. 8)  и .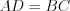
Периметр прямоугольника, смежные стороны которого равны  (длина) и  (ширина), находят по формуле: 
.

2. Квадратом называют прямоугольник, у которого все стороны равны (Рис. 9).
Периметр квадрата со стороной  находят по формуле: .

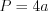Треугольники

Треугольником называют многоугольник, имеющий три вершины.

Классификация треугольников по сторонам

1. Равносторонним называют треугольник, у которого все стороны равны (Рис. 10).
2. Равнобедренным называют треугольник, у которого две стороны равны (Рис. 11). 
Равные стороны треугольника называют боковыми сторонами, а третью сторону называют основанием треугольника. 
Н а п р и м е р, на Рисунке 11 стороны  и  – боковые, а сторона  – основание треугольника .
3. Разносторонним называют треугольник, у которого все стороны имеют различную длину (Рис. 12).

Классификация треугольников по углам

1. Остроугольным называют треугольник, у которого все углы острые (Рис. 13).
2. Тупоугольным называют треугольник, у которого один из углов тупой (Рис. 14).
3. Прямоугольным называют треугольник, у которого один из углов прямой (Рис. 15).