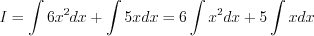Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
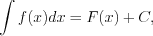 (7.1)
(7.1) (7.2)
(7.2)
 (7.3)
(7.3)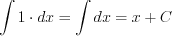 (7.4)
(7.4) 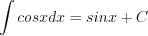 (7.11)
(7.11) 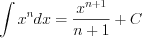 (7.5)
(7.5) 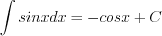 (7.12)
(7.12) 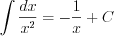 (7.6)
(7.6) 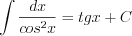 (7.13)
(7.13) 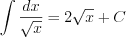 (7.7)
(7.7)  (7.14)
(7.14) 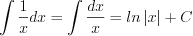 (7.8)
(7.8) 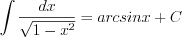 (7.15)
(7.15) 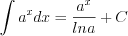 (7.9)
(7.9) 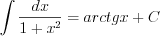 (7.16)
(7.16)  (7.10)
(7.10) 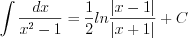 (7.17)
(7.17)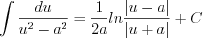 (7.18)
(7.18) 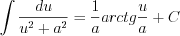 (7.19)
(7.19) 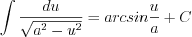 (7.20)
(7.20) 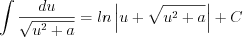 (7.21)
(7.21) 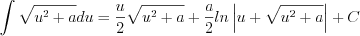 (7.22)
(7.22) 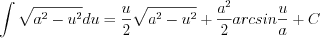 (7.23)
(7.23)
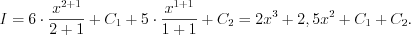
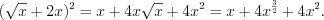
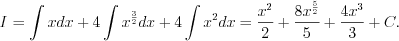
Функцию 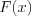 называют первообразной функции
называют первообразной функции  в промежутке
в промежутке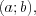 если при всех
если при всех 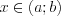 выполняется равенство
выполняется равенство 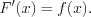 Если функция
Если функция 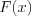 – первообразная функции
– первообразная функции  , то функция
, то функция 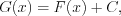 где
где  – произвольная постоянная, так же является первообразной функции
– произвольная постоянная, так же является первообразной функции 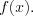
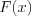 называют первообразной функции
называют первообразной функции  в промежутке
в промежутке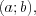 если при всех
если при всех 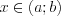 выполняется равенство
выполняется равенство 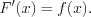 Если функция
Если функция 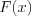 – первообразная функции
– первообразная функции  , то функция
, то функция 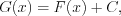 где
где  – произвольная постоянная, так же является первообразной функции
– произвольная постоянная, так же является первообразной функции 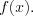
Неопределенным интегралом от функции  называют множество всех ее первообразных:
называют множество всех ее первообразных:
 называют множество всех ее первообразных:
называют множество всех ее первообразных: 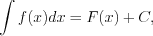 (7.1)
(7.1)где 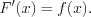 При этом функцию
При этом функцию  называют подынтегральной функцией, выражение
называют подынтегральной функцией, выражение  – подынтегральным выражением.
– подынтегральным выражением.
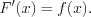 При этом функцию
При этом функцию  называют подынтегральной функцией, выражение
называют подынтегральной функцией, выражение  – подынтегральным выражением.
– подынтегральным выражением. Основные свойства неопределенного интеграла
1. Постоянный множитель можно выносить за знак интеграла:
 (7.2)
(7.2)
2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых:
 (7.3)
(7.3)Непосредственное интегрирование
Этот метод применяют в случае, когда при помощи свойств 7.2 и 7.3 (или одного из них) возможен переход непосредственно к одному или нескольким простейшим интегралам таблицы 

Таблица 1. Простейшие неопределенные интегралы
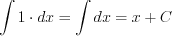 (7.4)
(7.4) 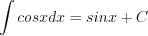 (7.11)
(7.11)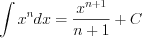 (7.5)
(7.5) 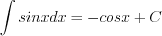 (7.12)
(7.12)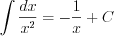 (7.6)
(7.6) 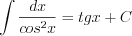 (7.13)
(7.13) 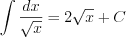 (7.7)
(7.7)  (7.14)
(7.14)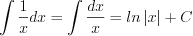 (7.8)
(7.8) 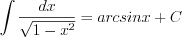 (7.15)
(7.15)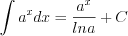 (7.9)
(7.9) 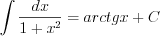 (7.16)
(7.16) (7.10)
(7.10) 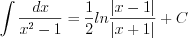 (7.17)
(7.17)В таблице  можно также везде вместо
можно также везде вместо  записать
записать 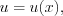 где
где 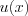 любая дифференцируемая функция. Например:
любая дифференцируемая функция. Например:
 можно также везде вместо
можно также везде вместо  записать
записать 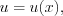 где
где 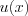 любая дифференцируемая функция. Например:
любая дифференцируемая функция. Например: Таблица 2. Неопределенные интегралы
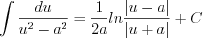 (7.18)
(7.18) 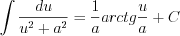 (7.19)
(7.19) 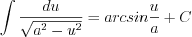 (7.20)
(7.20) 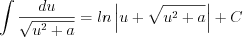 (7.21)
(7.21) 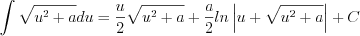 (7.22)
(7.22) 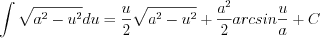 (7.23)
(7.23)Аналогично применяются и формулы таблицы 
Пример 1. Убедимся, что функция 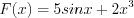 является первообразной функции
является первообразной функции 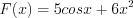 на области всех действительных чисел. Действительно,
на области всех действительных чисел. Действительно,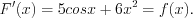 Функция
Функция 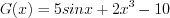 также является первообразной этой функции, так как
также является первообразной этой функции, так как 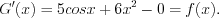
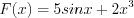 является первообразной функции
является первообразной функции 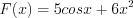 на области всех действительных чисел. Действительно,
на области всех действительных чисел. Действительно,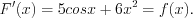 Функция
Функция 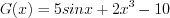 также является первообразной этой функции, так как
также является первообразной этой функции, так как 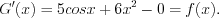
Пример 2. Убедимся, что равенство 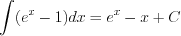 верное. Так как
верное. Так как 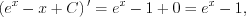 то, действительно, это равенство верное.
то, действительно, это равенство верное.
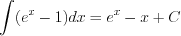 верное. Так как
верное. Так как 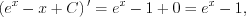 то, действительно, это равенство верное.
то, действительно, это равенство верное.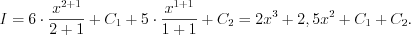
Поскольку сумма произвольных постоянных есть произвольная постоянная 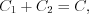 то, как правило, ответ записывают так:
то, как правило, ответ записывают так: 

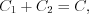 то, как правило, ответ записывают так:
то, как правило, ответ записывают так: 

1. Каждая из формул таблиц  и
и  справедлива только в области определения соответствующей функции.
справедлива только в области определения соответствующей функции.
 и
и  справедлива только в области определения соответствующей функции.
справедлива только в области определения соответствующей функции. 2. Многие интегралы можно найти непосредственно, если предварительно преобразовать подынтегральные функции. Например, чтобы найти интеграл  необходимо выполнить следующие преобразования:
необходимо выполнить следующие преобразования:
 необходимо выполнить следующие преобразования:
необходимо выполнить следующие преобразования: 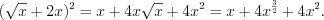
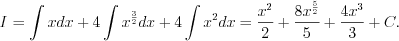
Непосредственное интегрирование
Метод подстановки


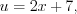 то согласно формуле
то согласно формуле 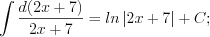
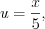 то согласно
то согласно 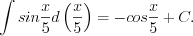
 и
и 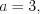 то согласно формуле
то согласно формуле 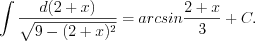
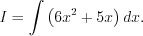 На основании свойств
На основании свойств