1. Касательная и нормаль графика функции
Уравнение касательной, проведенной к графику функции в точке
в точке 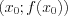 , имеет вид:
, имеет вид: 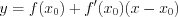 . (6.10)
. (6.10)Уравнение нормали , проведенной к графику функции
 в точке
в точке 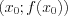 , имеет вид:
, имеет вид: 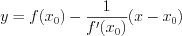 . (6.11)
. (6.11)
2. Приближенные вычисления значений функции
Приближенное значение
функции  в точке
в точке 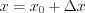 находят по формуле:
находят по формуле:
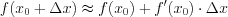 . (6.12)
. (6.12)
3.
Вычисление пределов функции
Правило Лопиталя-Бернулли
: если функции и
и  определены, дифференцируемы и являются бесконечно малыми или бесконечно большими в некоторой окрестности точки , то справедливо равенство:
определены, дифференцируемы и являются бесконечно малыми или бесконечно большими в некоторой окрестности точки , то справедливо равенство:
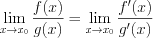 . (6.13)
. (6.13)
Правило 6.13 можно применять и в случаях, когда:
а) аргумент функции стремится к значению, которое не входит в ее область определения, например 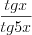 , при
, при 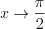 ;
;
б) при раскрытии неопределенности вида  , преобразовав разность в частное, например,
, преобразовав разность в частное, например, 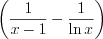 при
при 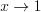 ;
;
в) при раскрытии неопределенности вида 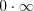 , преобразовав произведение в частное, например, функцию
, преобразовав произведение в частное, например, функцию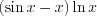 при
при 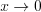 преобразуем так:
преобразуем так: 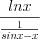 ;
;
г) при раскрытии неопределенностей вида 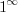 ,
, 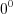 и
и 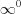 , выполнив предварительное логарифмирование по формуле
, выполнив предварительное логарифмирование по формуле
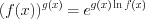 , например, функцию
, например, функцию 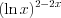 при
при 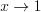 (неопределенность вида
(неопределенность вида 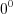 ) преобразуем так:
) преобразуем так: 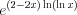 .
.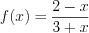 в точке с абсциссой
в точке с абсциссой 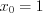 .
.Решение . 1. Найдем значение функции в точке
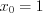 :
: 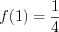 .
.2. Используя формулу
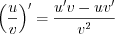 найдем производную функции:
найдем производную функции: 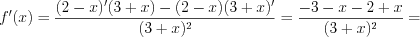

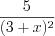 .
.3. Найдем значение производной в точке
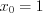 :
: 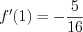 .
.4. Согласно формуле 6.10 запишем уравнение касательной:
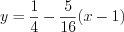 ,
, 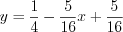 ,
, 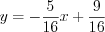 .
.Ответ :
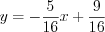 .
.
Пример 2. Найдите приближенно 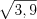 .
.
Решение . 1. Согласно формуле 6.12 запишем:
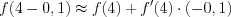
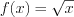 . Тогда
. Тогда 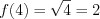 .
.3. Найдем ее производную:
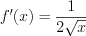 . Тогда
. Тогда 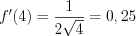 .
. 4. Получим:
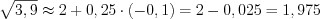 .
.Ответ :
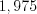 .
.Пример 3. Вычислите предел
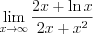 .
.Решение . Имеем неопределенность вида
 . Применим правило 6.13:
. Применим правило 6.13: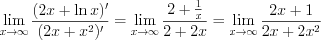 .
. Снова имеем неопределенность вида
 . Еще раз применим правило6.13:
. Еще раз применим правило6.13: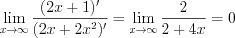 .
.Ответ : 0.
 и
и  , но при условии, что пред ел
, но при условии, что пред ел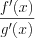 существует или равен бесконечности.
существует или равен бесконечности.2. Если частное
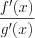 в свою очередь дает неопределенность вида
в свою очередь дает неопределенность вида  или
или  , то можно несколько раз применять правило Лопиталя-Бернулли, но при условии, что все пределы существуют.
, то можно несколько раз применять правило Лопиталя-Бернулли, но при условии, что все пределы существуют. 
