Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
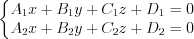 , (4.32)
, (4.32)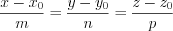 , (4.33)
, (4.33)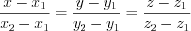 . (4.34)
. (4.34)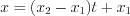 ,
, 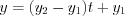 ,
, 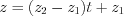 . (4.35)
. (4.35)
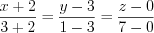 ,
, 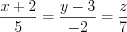 .
.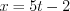 ,
, 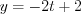 ,
, 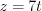 .
.
1. Общее уравнение прямой в пространстве имеет вид:
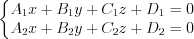 , (4.32)
, (4.32)2. Каноническое уравнение прямой имеет вид:
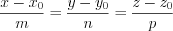 , (4.33)
, (4.33)где 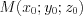 – точка, принадлежащая этой прямой, а
– точка, принадлежащая этой прямой, а 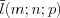 – направляющий вектор прямой.
– направляющий вектор прямой.
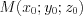 – точка, принадлежащая этой прямой, а
– точка, принадлежащая этой прямой, а 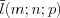 – направляющий вектор прямой.
– направляющий вектор прямой.3. Если известны координаты точек 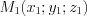 и
и 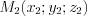 , принадлежащих прямой, то уравнение этой прямой можно найти по формуле:
, принадлежащих прямой, то уравнение этой прямой можно найти по формуле:
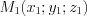 и
и 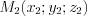 , принадлежащих прямой, то уравнение этой прямой можно найти по формуле:
, принадлежащих прямой, то уравнение этой прямой можно найти по формуле: 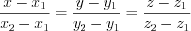 . (4.34)
. (4.34)4. Чтобы записать параметрические уравнения прямой, можно воспользоваться равенством 4.33 или 4.34 Например, полагая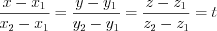 , получим:
, получим:
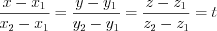 , получим:
, получим: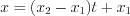 ,
, 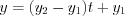 ,
, 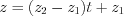 . (4.35)
. (4.35)Пример 1. Запишите параметрические уравнения прямой, проходящей через точки 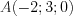 и
и 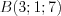 .
.
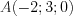 и
и 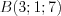 .
.Решение. Согласно формуле 4.34 запишем:
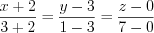 ,
, 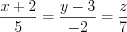 .
.Полагая 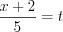 ,
, 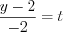 ,
, 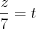 , получим:
, получим:
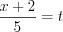 ,
, 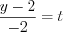 ,
, 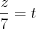 , получим:
, получим: 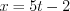 ,
, 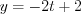 ,
, 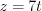 .
.Ответ: 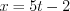 ,
, 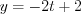 ,
, 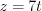 .
.
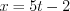 ,
, 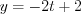 ,
, 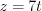 .
.

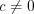 :
: 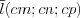 .
.