Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
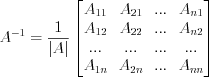 , (1.15)
, (1.15) . (1.16)
. (1.16)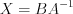 . (1.17)
. (1.17)
 ;
; 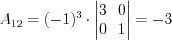 ;
; 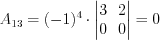 ;
; 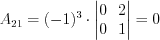 ;
;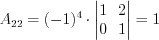 ;
; 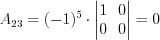 ;
;  ;
;  ;
;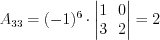 .
.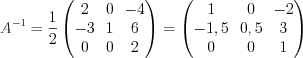 .
.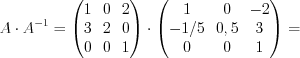

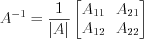 .
. .
. ;
; 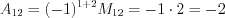 ;
;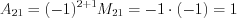 ;
; 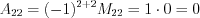 .
.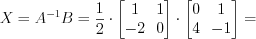
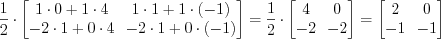 .
.
Дана квадратная матрица 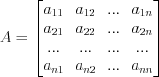 .
.
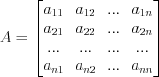 .
.Квадратная матрица 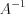 является обратной к квадратной матрице
является обратной к квадратной матрице  , если
, если 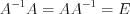 .
.
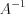 является обратной к квадратной матрице
является обратной к квадратной матрице  , если
, если 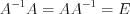 .
. Матрицу, обратную к матрице  , находят по формуле:
, находят по формуле:
 , находят по формуле:
, находят по формуле: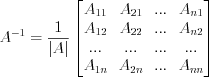 , (1.15)
, (1.15)где 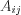 – алгебраическое дополнение элемента матрицы
– алгебраическое дополнение элемента матрицы  ,
, 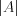 – определитель матрицы
– определитель матрицы  .
.
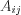 – алгебраическое дополнение элемента матрицы
– алгебраическое дополнение элемента матрицы  ,
, 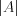 – определитель матрицы
– определитель матрицы  .
.Решение матричных уравнений
1. Если матричное уравнение имеет вид 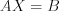 , то матрицу
, то матрицу  находят по формуле
находят по формуле
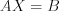 , то матрицу
, то матрицу  находят по формуле
находят по формуле . (1.16)
. (1.16)2. Если матричное уравнение имеет вид  , то матрицу
, то матрицу  находят по формуле
находят по формуле
 , то матрицу
, то матрицу  находят по формуле
находят по формуле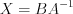 . (1.17)
. (1.17)Пример 1. Найдите матрицу, обратную матрице  .
.
 .
.Решение. По формуле 1.12 найдем определитель данной матрицы: 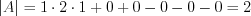 .
.
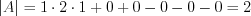 .
. ;
; 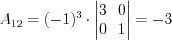 ;
; 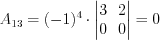 ;
; 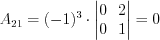 ;
;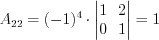 ;
; 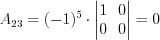 ;
;  ;
;  ;
;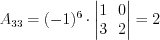 .
.По формуле 1.15 получим:
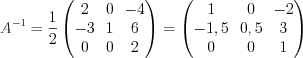 .
.Проверка:
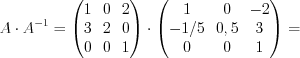

Ответ: 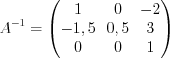 .
.
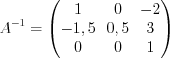 .
.Пример 2. Решите матричное уравнение 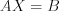 , если
, если  , а
, а  .
.
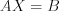 , если
, если  , а
, а  .
.1. Найдем матрицу, обратную к матрице  , по формуле:
, по формуле:
 , по формуле:
, по формуле: 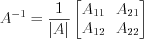 .
.Найдем определитель матрицы  :
:
 :
:  .
. ;
; 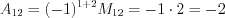 ;
;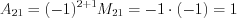 ;
; 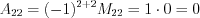 .
.Запишем:  .
.
 .
.2. Найдем матрицу  :
:
 :
: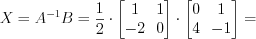
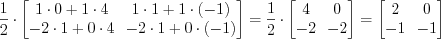 .
.Ответ: 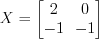 .
.
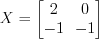 .
.Если определитель матрицы равен нулю, то говорят, что матрица вырождена. Вырожденная матрица обратной матрицы не имеет.
Обратная матрица


