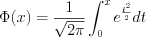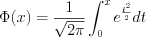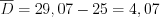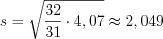Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
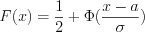 . (11.21)
. (11.21)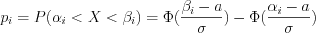 . (11.22)
. (11.22) 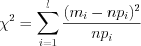 . (11.23)
. (11.23)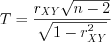 . (11.24)
. (11.24) 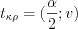 . (11.25)
. (11.25)
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.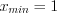 ,
, 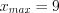 ,
,  ,
, 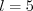 ,
, 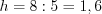 .
. 
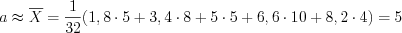 – средняя оценка.
– средняя оценка.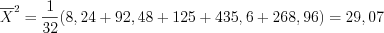 .
.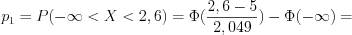
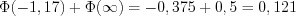 ;
;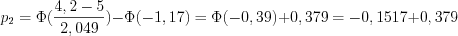
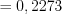 ;
;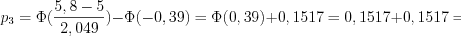
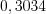 ;
;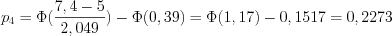 ;
;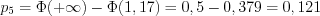 .
.
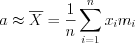 . (11.10)
. (11.10)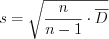 . (11.12)
. (11.12)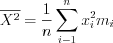 . (11.4)
. (11.4) - число степеней свободы,
- число степеней свободы,  - уровень значимости.
- уровень значимости.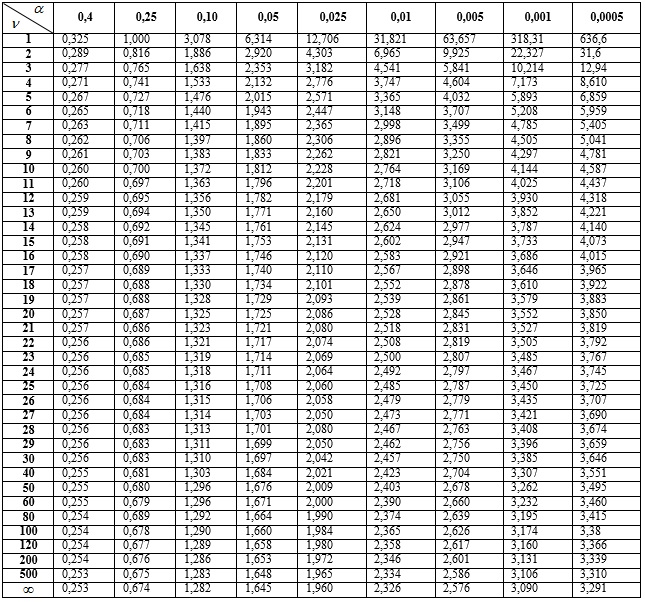
Статистическими гипотезами называют предположения, выдвигаемые на основании выборочных исследований относительно характера или параметров распределения случайной величины в генеральной совокупности.
Гипотеза называется параметрической, если в ней содержится некоторое утверждение относительно параметра известного распределения.
Гипотеза называется непараметрической, если в ней содержится утверждение относительно вида распределения.
Как правило, выдвигают основную (нулевую) гипотезу и альтернативную гипотезу  , которая является логическим отрицанием гипотезы
, которая является логическим отрицанием гипотезы  .
.
 , которая является логическим отрицанием гипотезы
, которая является логическим отрицанием гипотезы 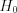 .
. Проверка гипотезы о нормальном распределении генеральной совокупности
Приведем алгоритм проверки гипотезы 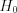 о согласии выборочного распределения с законом нормального распределения
о согласии выборочного распределения с законом нормального распределения  при уровне значимости
при уровне значимости  .
.
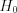 о согласии выборочного распределения с законом нормального распределения
о согласии выборочного распределения с законом нормального распределения  при уровне значимости
при уровне значимости  .
. Гипотезы: 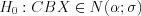 ;
; 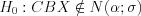 .
.
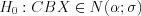 ;
; 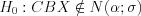 .
.1. Построим интервальный вариационный ряд для значений признака  – число интервалов;
– число интервалов;  – число значений признака
– число значений признака  , попавших в
, попавших в  --й интервал;
--й интервал;  – объем выборки .
– объем выборки .
 – число интервалов;
– число интервалов;  – число значений признака
– число значений признака  , попавших в
, попавших в  --й интервал;
--й интервал;  – объем выборки .
– объем выборки .2. Найдем точечные оценки параметров распределения: 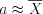 и
и 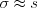 .
.
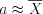 и
и 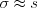 .
.3. Запишем гипотетическую функцию нормального распределения:
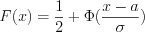 . (11.21)
. (11.21)4. Вычислим вероятности 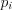 попадания
попадания  в частичный
в частичный  -й интервал
-й интервал 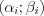 :
:
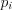 попадания
попадания  в частичный
в частичный  -й интервал
-й интервал 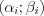 :
: 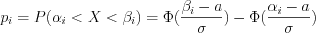 . (11.22)
. (11.22) 5. Вычислим теоретические частоты 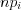 .
.
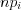 .
. 6. Найдем  - статистику Пирсона:
- статистику Пирсона:
 - статистику Пирсона:
- статистику Пирсона: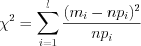 . (11.23)
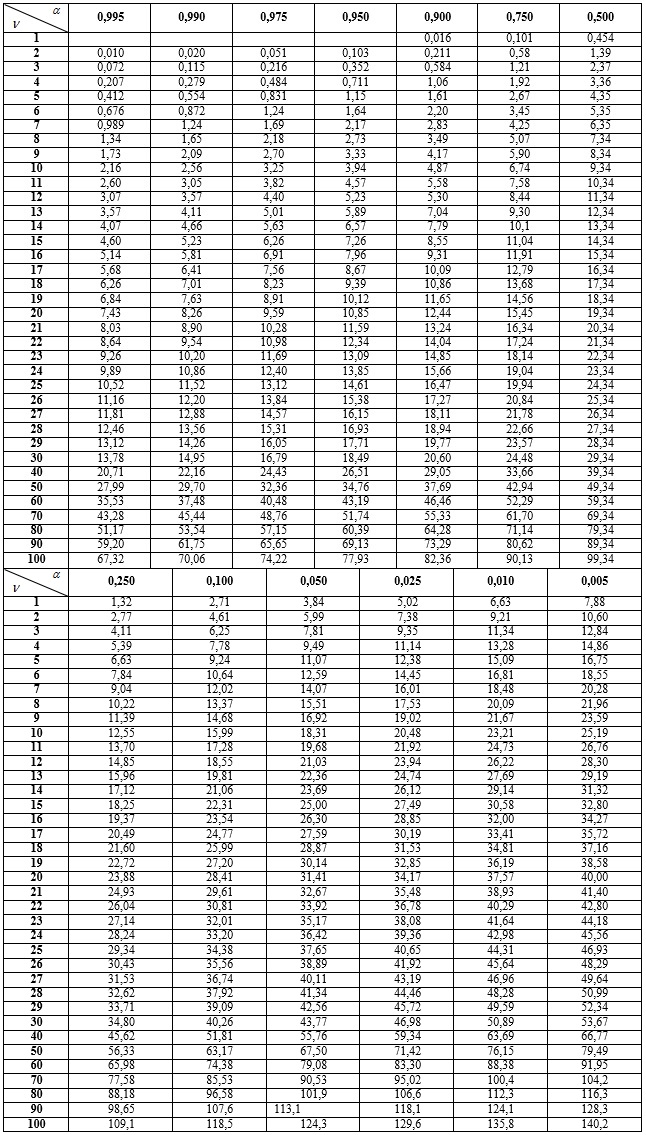
. (11.23)7. По таблице  - распределения при заданном уровне значимости
- распределения при заданном уровне значимости  и числу степеней свободы
и числу степеней свободы  (
(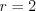 – число параметров проверяемого закона) найдем
– число параметров проверяемого закона) найдем 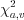 .
.
 - распределения при заданном уровне значимости
- распределения при заданном уровне значимости  и числу степеней свободы
и числу степеней свободы  (
(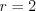 – число параметров проверяемого закона) найдем
– число параметров проверяемого закона) найдем 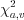 .
.8. Сравним  и
и 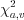 :
:
 и
и 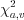 :
:1) если 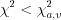 , то гипотеза
, то гипотеза 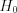 принимается;
принимается;
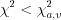 , то гипотеза
, то гипотеза 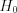 принимается;
принимается; 2) если 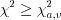 , то гипотеза
, то гипотеза 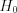 отвергается.
отвергается.
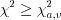 , то гипотеза
, то гипотеза 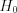 отвергается.
отвергается.Проверка гипотезы об отсутствии корреляционной связи
Из генеральной совокупности 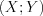 , имеющей нормальное распределение, извлечена выборка объема
, имеющей нормальное распределение, извлечена выборка объема  и для нее найден выборочный коэффициент корреляции
и для нее найден выборочный коэффициент корреляции  .
.
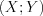 , имеющей нормальное распределение, извлечена выборка объема
, имеющей нормальное распределение, извлечена выборка объема  и для нее найден выборочный коэффициент корреляции
и для нее найден выборочный коэффициент корреляции  .
. Гипотезы: 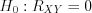 ;
; 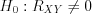 .
.
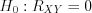 ;
; 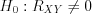 .
.Проверим нулевую гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности.
1. Вычислим наблюдаемое значение критерия  :
:
 :
: 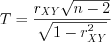 . (11.24)
. (11.24)2. По заданному уровню значимости  и числу степеней свободы
и числу степеней свободы 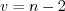 по таблице критических точек распределения Стьюдента находим критическую точку односторонней критической области:
по таблице критических точек распределения Стьюдента находим критическую точку односторонней критической области:
 и числу степеней свободы
и числу степеней свободы 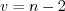 по таблице критических точек распределения Стьюдента находим критическую точку односторонней критической области:
по таблице критических точек распределения Стьюдента находим критическую точку односторонней критической области: 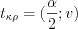 . (11.25)
. (11.25)3. Сравниваем  и
и 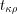 :
:
 и
и 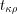 :
: 1) если 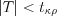 , то гипотезу
, то гипотезу 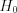 принимаем;
принимаем;
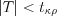 , то гипотезу
, то гипотезу 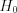 принимаем;
принимаем; 2) если  , то гипотезу
, то гипотезу 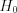 отклоняем.
отклоняем.
 , то гипотезу
, то гипотезу 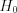 отклоняем.
отклоняем.Пример 1. Из всех студентов факультета было случайным образом выбрано 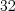 человека и выписаны их экзаменационные оценки по дисциплине «Высшая математика»:
человека и выписаны их экзаменационные оценки по дисциплине «Высшая математика»:
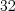 человека и выписаны их экзаменационные оценки по дисциплине «Высшая математика»:
человека и выписаны их экзаменационные оценки по дисциплине «Высшая математика»: ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.Необходимо проверить гипотезу 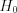 о согласии выборочного распределения с законом нормального распределения
о согласии выборочного распределения с законом нормального распределения  при уровне значимости
при уровне значимости 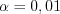 .
.
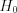 о согласии выборочного распределения с законом нормального распределения
о согласии выборочного распределения с законом нормального распределения  при уровне значимости
при уровне значимости 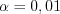 .
.Решение. 1. Построим интервальный вариационный ряд для значений признака  :
:
 :
: 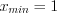 ,
, 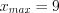 ,
,  ,
, 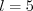 ,
, 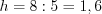 .
. 
2. Найдем точечные оценки параметров распределения.
По формуле 11.10 получим:
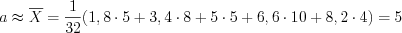 – средняя оценка.
– средняя оценка.По формуле 11.4 получим:
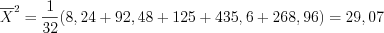 .
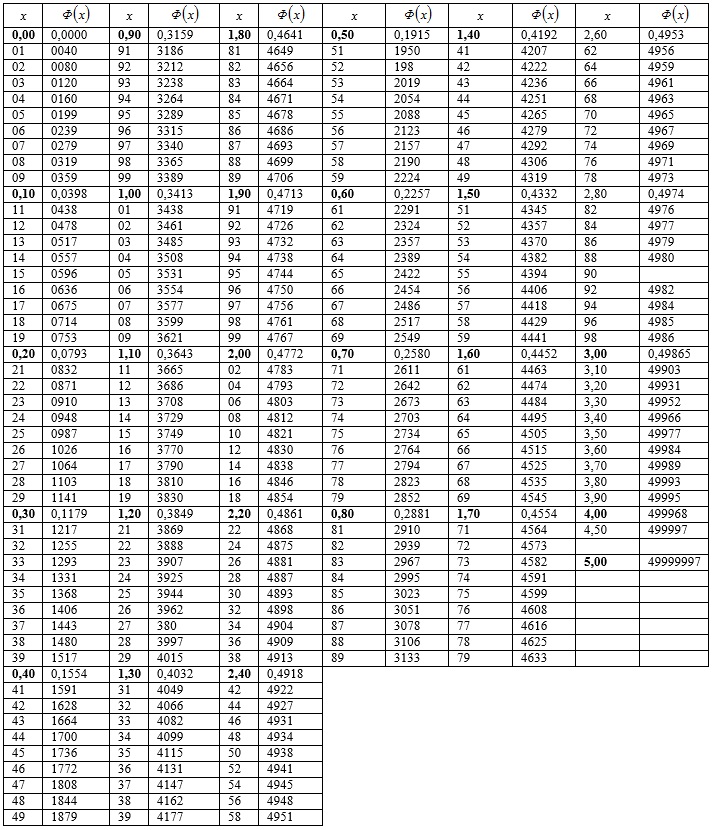
.3. По формуле 11.22 и таблице значений функции Лапласа (см. вкладку Обратите внимание) вычислим вероятности 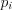 попадания
попадания  в частичный
в частичный  -й интервал:
-й интервал:
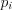 попадания
попадания  в частичный
в частичный  -й интервал:
-й интервал: 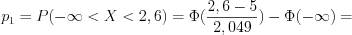
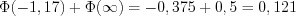 ;
;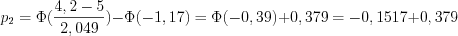
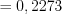 ;
;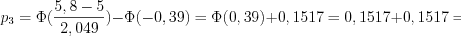
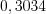 ;
;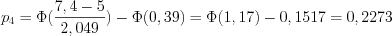 ;
;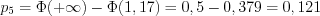 .
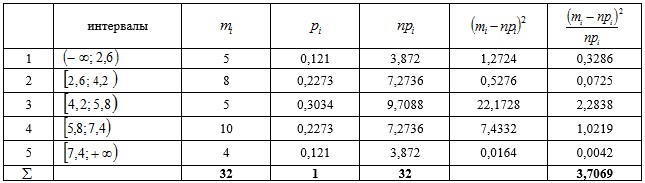
.4. Все расчеты представим в таблице:

5. По формуле 11.23 получим: 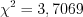 . По таблице
. По таблице  -распределения (см. вкладку Обратите внимание) при заданном уровне значимости
-распределения (см. вкладку Обратите внимание) при заданном уровне значимости 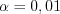 и числу степеней свободы
и числу степеней свободы  получим:
получим:  . Поскольку
. Поскольку  , то гипотеза
, то гипотеза 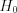 принимается. Следовательно, оценки студентов распределены нормально, а функция распределения 11.21 имеет вид:
принимается. Следовательно, оценки студентов распределены нормально, а функция распределения 11.21 имеет вид: 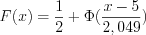 .
.
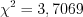 . По таблице
. По таблице  -распределения (см. вкладку Обратите внимание) при заданном уровне значимости
-распределения (см. вкладку Обратите внимание) при заданном уровне значимости 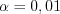 и числу степеней свободы
и числу степеней свободы  получим:
получим:  . Поскольку
. Поскольку  , то гипотеза
, то гипотеза 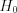 принимается. Следовательно, оценки студентов распределены нормально, а функция распределения 11.21 имеет вид:
принимается. Следовательно, оценки студентов распределены нормально, а функция распределения 11.21 имеет вид: 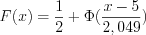 .
. Ответ: 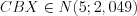 .
.
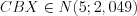 .
.Пример 2. Проверьте на уровне значимость 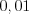 гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности, если выборочный коэффициент корреляции равен
гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности, если выборочный коэффициент корреляции равен 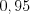 , а объем выборки равен
, а объем выборки равен 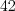 .
.
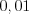 гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности, если выборочный коэффициент корреляции равен
гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности, если выборочный коэффициент корреляции равен 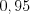 , а объем выборки равен
, а объем выборки равен 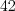 .
.Решение. 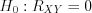 ;
; 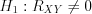 .
.
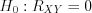 ;
; 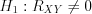 .
.2. По заданному уровню значимости 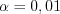 и числу степеней свободы
и числу степеней свободы  по формуле 11.25 и таблице критических точек распределения Стьюдента (см. вкладку Обратите внимание) находим критическую точку односторонней критической области:
по формуле 11.25 и таблице критических точек распределения Стьюдента (см. вкладку Обратите внимание) находим критическую точку односторонней критической области: 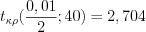 .
.
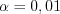 и числу степеней свободы
и числу степеней свободы  по формуле 11.25 и таблице критических точек распределения Стьюдента (см. вкладку Обратите внимание) находим критическую точку односторонней критической области:
по формуле 11.25 и таблице критических точек распределения Стьюдента (см. вкладку Обратите внимание) находим критическую точку односторонней критической области: 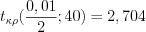 .
.3. Так как если 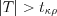 , то гипотезу
, то гипотезу 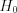 отклоняем и принимаем гипотезу
отклоняем и принимаем гипотезу 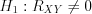 .
.
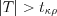 , то гипотезу
, то гипотезу 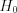 отклоняем и принимаем гипотезу
отклоняем и принимаем гипотезу 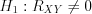 .
. Ответ: 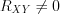 .
.
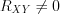 .
.1. Проверяя гипотезу о нормальном распределении  , первый промежуток интервального вариационного ряда
, первый промежуток интервального вариационного ряда 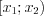 заменяем интервалом
заменяем интервалом 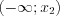 , а последний отрезок
, а последний отрезок ![[x_{k-1};x_k] LaTeX formula: [x_{k-1};x_k]](/uploads/formulas/ee6706256e990bad97478b58f96f31b31169e41f.1.1.png) – промежутком
– промежутком 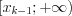 .
.
 , первый промежуток интервального вариационного ряда
, первый промежуток интервального вариационного ряда 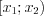 заменяем интервалом
заменяем интервалом 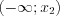 , а последний отрезок
, а последний отрезок ![[x_{k-1};x_k] LaTeX formula: [x_{k-1};x_k]](/uploads/formulas/ee6706256e990bad97478b58f96f31b31169e41f.1.1.png) – промежутком
– промежутком 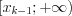 .
. 2. Точечная оценка математического ожидания:
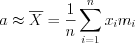 . (11.10)
. (11.10)Точечная оценка среднего квадратического отклонения (эмпирический стандарт):
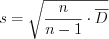 . (11.12)
. (11.12)где 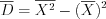 , (11.3)
, (11.3)
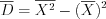 , (11.3)
, (11.3) 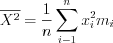 . (11.4)
. (11.4)3. Распределение Стьюдента (t-распределение)
 - число степеней свободы,
- число степеней свободы,  - уровень значимости.
- уровень значимости.
4. Таблица 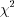 -распределение
-распределение
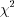 -распределение
-распределение
5. Таблица значений функции