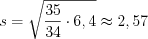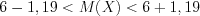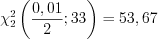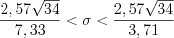Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
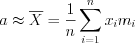 . (11.10)
. (11.10)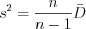 ; (11.11)
; (11.11)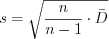 . (11.12)
. (11.12)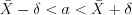 . (11.13)
. (11.13)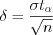 , (11.14)
, (11.14)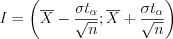 . (11.15)
. (11.15)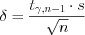 , (11.16)
, (11.16) . (11.17)
. (11.17)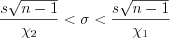 , (11.18)
, (11.18)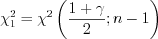 , (11.19)
, (11.19)  . (11.20)
. (11.20)


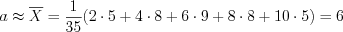 .
.
 – число степеней свободы,
– число степеней свободы,  – уровень значимости.
– уровень значимости.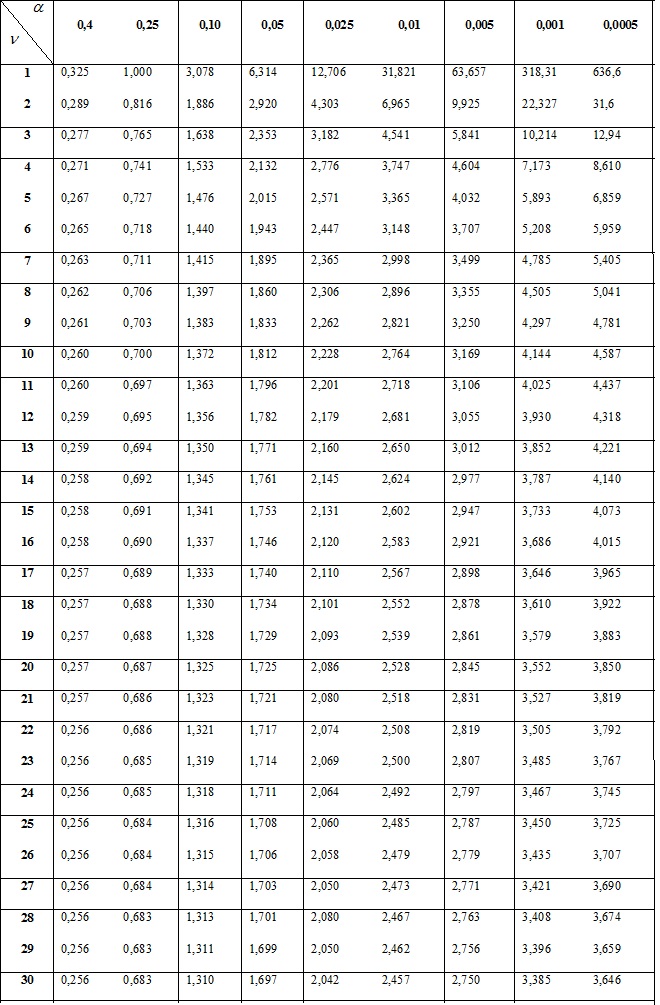
Рассмотрим случайную величину  , имеющую нормальное распределение:
, имеющую нормальное распределение: 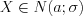 .
.
 , имеющую нормальное распределение:
, имеющую нормальное распределение: 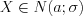 .
. Точечные оценки.
Точечной оценкой математического ожидания  генеральной совокупности является выборочная средняя:
генеральной совокупности является выборочная средняя:
 генеральной совокупности является выборочная средняя:
генеральной совокупности является выборочная средняя: 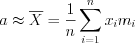 . (11.10)
. (11.10)Точечной оценкой среднего квадратического отклонения  является эмпирический стандарт
является эмпирический стандарт  .
.
 является эмпирический стандарт
является эмпирический стандарт  .
.Исправленную дисперсию находят по формуле:
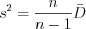 ; (11.11)
; (11.11)Эмпирический стандарт находят по формуле:
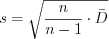 . (11.12)
. (11.12)где  ,
, 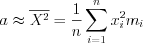
 ,
, 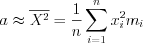
Интервальные оценки
1. Доверительный интервал для оценки математического ожидания:
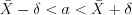 . (11.13)
. (11.13)Если среднее квадратическое отклонение  известно, то
известно, то
 известно, то
известно, то 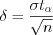 , (11.14)
, (11.14)где 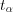 – корень уравнения
– корень уравнения 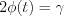 ,
,  – объем выборки,
– объем выборки,  – доверительная вероятность.
– доверительная вероятность.
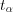 – корень уравнения
– корень уравнения 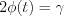 ,
,  – объем выборки,
– объем выборки,  – доверительная вероятность.
– доверительная вероятность.Доверительный интервал, который покрывает неизвестный параметр  с надежностью
с надежностью 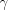 , имеет вид:
, имеет вид:
 с надежностью
с надежностью 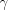 , имеет вид:
, имеет вид: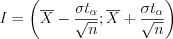 . (11.15)
. (11.15)Если среднее квадратическое отклонение  неизвестно, то
неизвестно, то
 неизвестно, то
неизвестно, то 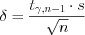 , (11.16)
, (11.16)где 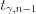 – аргумент функции Стьюдента (см. вкладку Обратите внимание),
– аргумент функции Стьюдента (см. вкладку Обратите внимание),  – точечная оценка
– точечная оценка  .
.
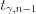 – аргумент функции Стьюдента (см. вкладку Обратите внимание),
– аргумент функции Стьюдента (см. вкладку Обратите внимание),  – точечная оценка
– точечная оценка  .
. Доверительный интервал, который покрывает неизвестный параметр  с надежностью
с надежностью 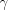 , имеет вид:
, имеет вид:
 с надежностью
с надежностью 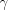 , имеет вид:
, имеет вид: . (11.17)
. (11.17)2. Доверительный интервал для оценки среднего квадратического отклонения нормально распределенной  , если
, если  и
и  неизвестны:
неизвестны:
 , если
, если  и
и  неизвестны:
неизвестны: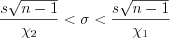 , (11.18)
, (11.18)где
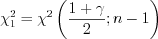 , (11.19)
, (11.19)  . (11.20)
. (11.20)Значения 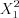 и
и 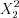 определяются по таблице
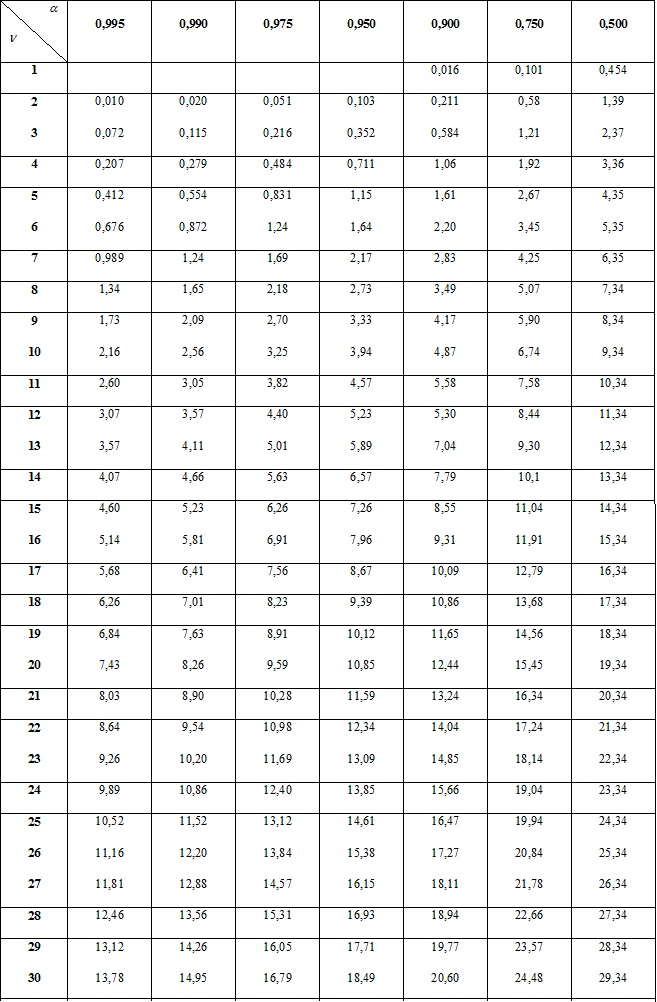
определяются по таблице 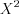 -распределения (см. вкладку Обратите внимание).
-распределения (см. вкладку Обратите внимание).
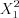 и
и 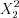 определяются по таблице
определяются по таблице 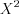 -распределения (см. вкладку Обратите внимание).
-распределения (см. вкладку Обратите внимание).Пример. Найдите точечные и интервальные оценки параметров нармального распределения:

Решение. 1. Найдем точечные оценки параметров распределения.
В качестве значений 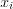 возьмем середины интервалов:
возьмем середины интервалов:
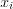 возьмем середины интервалов:
возьмем середины интервалов:
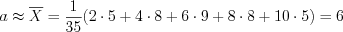 .
.По формуле  получим:
получим:  .
.
 получим:
получим:  .
.По формуле 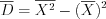 получим:
получим: 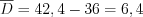 .
.
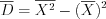 получим:
получим: 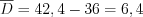 .
.2. С вероятностью 99% найдем доверительный интервал для математического ожидания СВХ.
3. С вероятностью 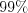 найдем доверительный интервал для среднего квадратического отклонения
найдем доверительный интервал для среднего квадратического отклонения  .
.
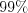 найдем доверительный интервал для среднего квадратического отклонения
найдем доверительный интервал для среднего квадратического отклонения  .
. По формуле 11.19 и таблице значений 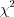 -распределения (см. вкладку Обратите внимание) получим:
-распределения (см. вкладку Обратите внимание) получим: 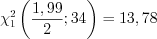 , откуда
, откуда 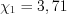 .
.
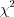 -распределения (см. вкладку Обратите внимание) получим:
-распределения (см. вкладку Обратите внимание) получим: 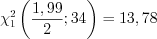 , откуда
, откуда 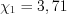 .
.Ответ: 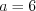 ;
; 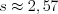 ; с надежностью
; с надежностью 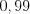 ;
; 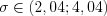 с надежностью
с надежностью 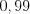 .
.
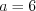 ;
; 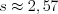 ; с надежностью
; с надежностью 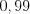 ;
; 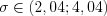 с надежностью
с надежностью 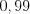 .
.1. Случайная величина  распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами  и
и  , если ее функция распределения имеет вид:
, если ее функция распределения имеет вид:  . Записывают:
. Записывают: 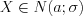 , причем
, причем 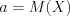 ,
, 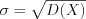 .
.
 распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами  и
и  , если ее функция распределения имеет вид:
, если ее функция распределения имеет вид:  . Записывают:
. Записывают: 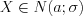 , причем
, причем 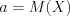 ,
, 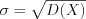 .
. 2. Распределение Стьюдента (t-распределение)
 – число степеней свободы,
– число степеней свободы,  – уровень значимости.
– уровень значимости.
3. Таблица 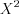 - распределение
- распределение
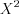 - распределение
- распределение