Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты


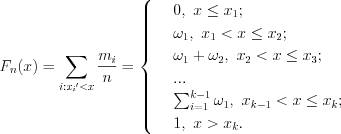 (11.1)
(11.1)
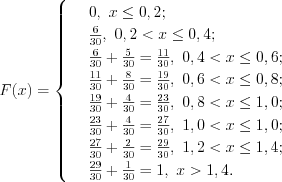



































 .
.

































 .
.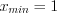 ,
, 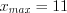 ,
,  ,
, 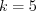 ,
, 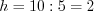 .
.
Математическая статистика изучает методы сбора, обработки и интерпретации результатов опытов (экспериментов).
Генеральной совокупностью называют множество однородных объектов с характерными для них признаками.
Выборочной совокупностью (выборкой) называют подмножество объектов генеральной совокупности, извлеченных из нее случайным образом.
Случайная величина  – наблюдаемые (полученные экспериментально) значения некоторого признака, характерного для всех объектов совокупности.
– наблюдаемые (полученные экспериментально) значения некоторого признака, характерного для всех объектов совокупности.
 – наблюдаемые (полученные экспериментально) значения некоторого признака, характерного для всех объектов совокупности.
– наблюдаемые (полученные экспериментально) значения некоторого признака, характерного для всех объектов совокупности. Статистические ряды
Различают дискретные и интервальные статистические ряды.
Рассмотрим выборку 
 ,
,  , …,
, …, 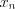 объема
объема  .
.

 ,
,  , …,
, …, 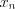 объема
объема  .
.1. Дискретный вариационный ряд распределения случайной величины  имеет вид:
имеет вид:
 имеет вид:
имеет вид: Таблица 1

Чтобы построить дискретный вариационный ряд, необходимо:
1) расположить значения признака  (варианты) в порядке возрастания:
(варианты) в порядке возрастания: 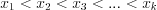 ;
;
 (варианты) в порядке возрастания:
(варианты) в порядке возрастания: 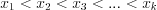 ;
; 2) найти частоты 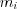 вариант (количество значений вариант
вариант (количество значений вариант 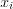 );
);
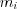 вариант (количество значений вариант
вариант (количество значений вариант 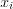 );
); 3) найти относительные частоты 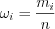 вариант.
вариант.
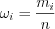 вариант.
вариант. 2. Интервальный вариационный ряд распределения случайной величины  имеет вид:
имеет вид:
 имеет вид:
имеет вид: Таблица 2

Чтобы построить интервальный вариационный ряд, необходимо:
1) найти размах вариации: 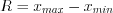 , где
, где  ,
, 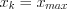 ;
;
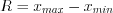 , где
, где  ,
, 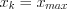 ;
;2) определить количество интервалов:  ;
;
 ;
; 3) найти длину интервала: 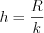 ;
;
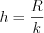 ;
; 4) найти частоты вариант на интервалах: 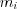 ;
;
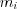 ;
; 5) найти относительные частоты вариант на интервалах: 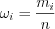 .
.
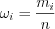 .
.Функция распределения выборки
Эмпирической функцией распределения выборки, представленной в таблице 1, называют функцию вида:
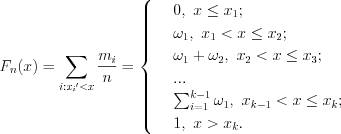 (11.1)
(11.1)Графическое представление выборки
1. Полигоном частот выборки (таблица 1) называют ломаную линию, соединяющую на координатной плоскости точки вида 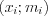 ,
, 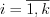 ,
,
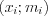 ,
, 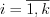 ,
, а полигоном относительных частот – ломаную линию, соединяющую на координатной плоскости точки вида 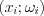 ,
, 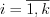 .
.
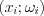 ,
, 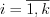 .
.2. Гистограммой частот выборки (таблица 2) называют столбчатую диаграмму, состоящую из прямоугольников, основаниями которых являются длины интервалов, которые содержат значения вариант, высотами – частоты данных интервалов,
а гистограммой относительных частот – диаграмму, состоящую из прямоугольников, основаниями которых являются длины интервалов, которые содержат значения вариант, высотами – относительные частоты данных интервалов.
Пример 1. Даны следующие значения  :
: 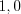






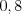
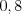
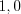
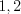
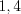

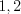
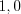



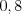


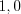
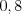






 .
.
 :
: 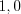






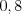
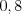
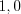
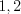
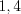

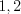
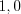



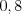


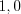
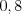






 .
.Необходимо:
1) построить дискретный вариационный ряд;
2) записать и построить эмпирическую функцию распределения случайной величины;
3) построить полигон частот.
Решение. 1. Расположим значения признака в порядке возрастания: 


















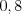
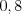
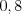
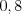
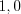
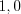
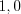
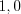
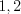
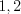
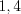 .
.



















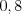
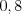
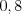
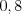
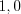
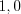
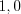
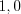
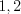
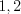
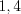 .
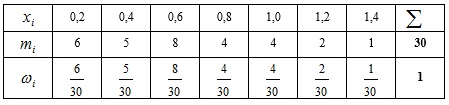
.Построим дискретный вариационный ряд:

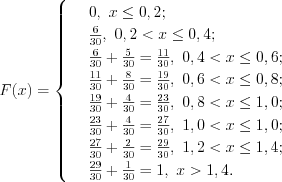
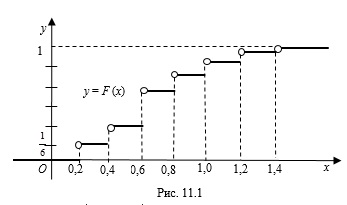
Построим эмпирическую функцию распределения  (рис. 11.1):
(рис. 11.1):
 (рис. 11.1):
(рис. 11.1):
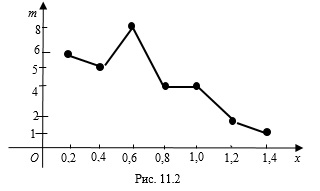
3. Построим полигон частот (рис. 11.2).

Пример 2. Даны следующие значения  :
:
 :
: 


































 .
.Необходимо: 1) построить интервальный вариационный ряд;
2) построить гистограмму относительных частот.
Решение. Расположим значения признака в порядке возрастания:


































 .
.1. Построим интервальный вариационный ряд:
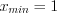 ,
, 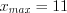 ,
,  ,
, 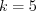 ,
, 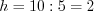 .
.
2. Построим гистограмму относительных частот (рис. 11.3).

1. Сумма частот всегда равна объему выборки  , а сумма относительных частот всегда равна единице:
, а сумма относительных частот всегда равна единице: 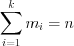 ;
; 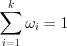 .
.
 , а сумма относительных частот всегда равна единице:
, а сумма относительных частот всегда равна единице: 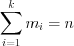 ;
; 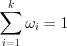 .
.2. Полигон частот и относительных частот строят для дискретного вариационного ряда.
3. Гистограмму частот и относительных частот строят для интервального вариационного ряда.

