Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (10.4)
. (10.4)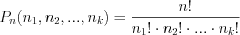 , (10.4.1)
, (10.4.1)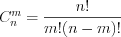 . (10.5)
. (10.5) . (10.6)
. (10.6)
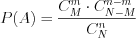 . (10.7)
. (10.7)
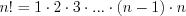 ;
; 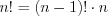 ; по определению полагают
; по определению полагают 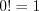 .
.
Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используют и для подсчета числа равновозможных событий.
Перестановки
Перестановками называют множества, состоящие из одних и тех же элементов и отличающихся друг от друга только их порядком. Число всевозможных перестановок из  различных элементов обозначают
различных элементов обозначают  и находят по формуле:
и находят по формуле:
 различных элементов обозначают
различных элементов обозначают  и находят по формуле:
и находят по формуле:  . (10.4)
. (10.4)Если некоторые элементы множества повторяются, то число перестановок с повторениями находят по формуле:
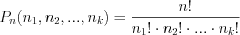 , (10.4.1)
, (10.4.1)где 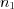 – число элементов одного вида,
– число элементов одного вида, 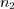 – число элементов другого вида и т. д.,
– число элементов другого вида и т. д.,  .
.
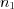 – число элементов одного вида,
– число элементов одного вида, 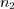 – число элементов другого вида и т. д.,
– число элементов другого вида и т. д.,  .
.Сочетания
Сочетаниями называют множества, содержащие  элементов из
элементов из  заданных, которые отличаются хотя бы одним элементом. Число сочетаний из
заданных, которые отличаются хотя бы одним элементом. Число сочетаний из  различных элементов по
различных элементов по  обозначают
обозначают 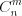 и находят по формуле:
и находят по формуле:
 элементов из
элементов из  заданных, которые отличаются хотя бы одним элементом. Число сочетаний из
заданных, которые отличаются хотя бы одним элементом. Число сочетаний из  различных элементов по
различных элементов по  обозначают
обозначают 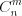 и находят по формуле:
и находят по формуле: 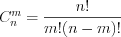 . (10.5)
. (10.5)Размещения
Размещениями называют множества, содержащие  элементов из
элементов из  заданных, которые отличаются либо составом элементов, либо их порядком. Число размещений из
заданных, которые отличаются либо составом элементов, либо их порядком. Число размещений из  различных элементов по
различных элементов по  обозначают
обозначают 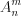 и находят по формуле:
и находят по формуле:
 элементов из
элементов из  заданных, которые отличаются либо составом элементов, либо их порядком. Число размещений из
заданных, которые отличаются либо составом элементов, либо их порядком. Число размещений из  различных элементов по
различных элементов по  обозначают
обозначают 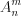 и находят по формуле:
и находят по формуле:  . (10.6)
. (10.6)Правила комбинаторики
Правило суммы. Если элемент  может быть выбран из множества элементов
может быть выбран из множества элементов  способами, а элемент
способами, а элемент  может быть выбран
может быть выбран  способами, то выбрать либо
способами, то выбрать либо  , либо
, либо  можно
можно  способами.
способами.
 может быть выбран из множества элементов
может быть выбран из множества элементов  способами, а элемент
способами, а элемент  может быть выбран
может быть выбран  способами, то выбрать либо
способами, то выбрать либо  , либо
, либо  можно
можно  способами.
способами. Правило произведения. Если элемент  может быть выбран из множества элементов
может быть выбран из множества элементов  способами и после каждого такого выбора другой элемент
способами и после каждого такого выбора другой элемент  может быть выбран
может быть выбран  способами, то выбрать
способами, то выбрать  и
и  в указанном порядке можно
в указанном порядке можно  способами.
способами.
 может быть выбран из множества элементов
может быть выбран из множества элементов  способами и после каждого такого выбора другой элемент
способами и после каждого такого выбора другой элемент  может быть выбран
может быть выбран  способами, то выбрать
способами, то выбрать  и
и  в указанном порядке можно
в указанном порядке можно  способами.
способами. Урновая схема
Из некоторого множества объема  разнородных элементов, среди которых
разнородных элементов, среди которых  элементов с определенными свойствами (особенных), выбирают
элементов с определенными свойствами (особенных), выбирают  элементов. Требуется определить вероятность того, что в выборке окажется
элементов. Требуется определить вероятность того, что в выборке окажется  особенных элементов.
особенных элементов.
 разнородных элементов, среди которых
разнородных элементов, среди которых  элементов с определенными свойствами (особенных), выбирают
элементов с определенными свойствами (особенных), выбирают  элементов. Требуется определить вероятность того, что в выборке окажется
элементов. Требуется определить вероятность того, что в выборке окажется  особенных элементов.
особенных элементов. Например, из урны, содержащей  шаров, среди которых
шаров, среди которых  белых, а остальные черные, выбирают
белых, а остальные черные, выбирают  шаров:
шаров:
 шаров, среди которых
шаров, среди которых  белых, а остальные черные, выбирают
белых, а остальные черные, выбирают  шаров:
шаров:
Вероятность того, что в выборке окажется  белых шаров (событие
белых шаров (событие  ) можно найти по формуле:
) можно найти по формуле:
 белых шаров (событие
белых шаров (событие  ) можно найти по формуле:
) можно найти по формуле: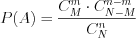 . (10.7)
. (10.7)Пример 1. Определим, сколькими способами можно рассадить за столом трех человек.
Ответ:  .
.
 .
. Пример 2. Определим, сколько слов можно получить, переставляя буквы в слове КНИГИ.
Решение. Поскольку имеем повторяющиеся элементы (две буквы И), то согласно формуле 10.4.1 получим:  .
.
 .
.Ответ:  .
.
 .
.Пример 3. Определим, сколькими способами можно выбрать три буквы из букв А, Б, О, Г, Е.
Решение. Поскольку при выборе трех букв не важен порядок их следования, то найдем число сочетаний по три элемента из пяти. Согласно формуле 10.5 получим: 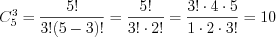 .
.
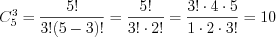 .
.Ответ:  .
.
 .
. Пример 4. Определим, сколько слов из четырех букв можно составить, имея буквы А, Б, О, Г, Е.
Решение. Поскольку при составлении слов важен порядок следования букв, то найдем число размещений по четыре элемента из пяти. Согласно формуле 10.6 получим: 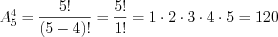 .
.
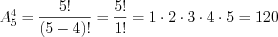 .
.Ответ:  .
.
 .
.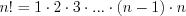 ;
; 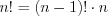 ; по определению полагают
; по определению полагают 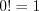 .
.