Функцией  называют такую зависимость переменной
называют такую зависимость переменной  от переменной
от переменной  , при которой каждому допустимому значению
, при которой каждому допустимому значению  соответствует
единственное значение
соответствует
единственное значение  .
.
Переменную  называют независимой переменной или
аргументом функции, а переменную
называют независимой переменной или
аргументом функции, а переменную  – зависимой от
– зависимой от  переменной или значением функции.
переменной или значением функции.
 называют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек вида
называют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек вида 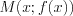 . График функции представляет собой некоторую линию на плоскости.
. График функции представляет собой некоторую линию на плоскости. Множество всех допустимых значений переменной
 образуют
область определения
функции. Множество всех допустимых значений переменной
образуют
область определения
функции. Множество всех допустимых значений переменной  образуют
область значений функции
. Область определения функции обозначают
образуют
область значений функции
. Область определения функции обозначают  , а область значений функции обозначают
, а область значений функции обозначают 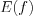 .
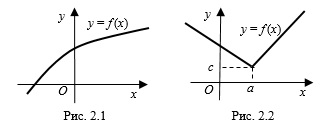
. Например: 1) областью определения функции, график которой изображен на рисунке 2.1, является множество всех действительных чисел и область значений этой функции – множество всех действительных чисел;
2) областью определения функции, график которой изображен на рисунке 2.2, является множество всех действительных чисел, а область ее значений – числа, принадлежащие промежутку
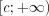 .
.
 возрастает
на промежутке
возрастает
на промежутке  , если для любых
, если для любых  и
и  , принадлежащих промежутку
, принадлежащих промежутку  , из неравенства
, из неравенства 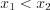 следует неравенство
следует неравенство 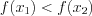 (рис. 2.3).
(рис. 2.3). 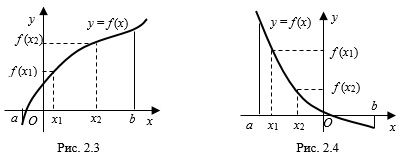
 убывает
на промежутке
убывает
на промежутке  , если для любых
, если для любых  и
и  , принадлежащих промежутку
, принадлежащих промежутку  , из неравенства
, из неравенства 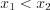 следует неравенство
следует неравенство 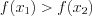 (рис. 2.4).
(рис. 2.4).Функцию называют монотонной , если она либо только возрастает, либо только убывает на всей своей области определения.
Например: 1) функция, график которой изображен на рисунке 2.1, монотонна, так как она возрастает на множестве всех действительных чисел; 2) функция, график которой изображен на рисунке 2.2 не монотонна, так как на промежутке
![(-\infty ;a] LaTeX formula: (-\infty ;a]](/uploads/formulas/7ded99d9c9ab77dae8e41675c495eac84a98e89b.1.1.png) она убывает, а на промежутке
она убывает, а на промежутке 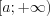 – возрастает.
– возрастает.Те значения переменной
 , при которых выполняется равенство
, при которых выполняется равенство  , называют нулями функции. Например, числа
, называют нулями функции. Например, числа 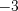 ,
, 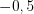 ,
, 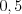 и
и  – нули функции, график которой изображен на рисунке 2.5.
– нули функции, график которой изображен на рисунке 2.5.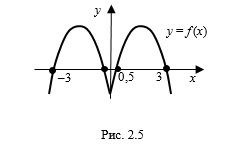
Например, функция, график которой изображен на рисунке 2.5, на промежутках
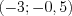 и
и 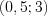 принимает положительные значения, а на промежутках
принимает положительные значения, а на промежутках 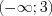 ,
, 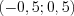 и
и 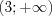 ее значения отрицательны.
ее значения отрицательны.Говорят, что числовое множество симметрично относительно точки
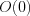 (начала отсчета) координатной прямой, если оно содержит только противоположные числа.
(начала отсчета) координатной прямой, если оно содержит только противоположные числа. Например, числовые множества
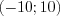 ,
, ![[-2,5;2,5] LaTeX formula: [-2,5;2,5]](/uploads/formulas/3616c0ccccbb3cba51759a07b146a0f3ddc95f7b.1.1.png) ,
, 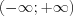 – симметричные, а множества
– симметричные, а множества 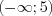 и
и 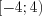 – несимметричные.
– несимметричные. Функция называется четной, если  – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и 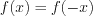 .
.
Функция называется
нечетной, если  – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и 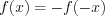 .
.
Например, функция 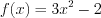 четная, а функция
четная, а функция 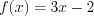 не является четной и не является нечетной, так как
не является четной и не является нечетной, так как 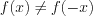 и
и 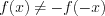 ни при одном значении переменной
ни при одном значении переменной  .
.
 , а график нечетной функции симметричен относительно точки
, а график нечетной функции симметричен относительно точки  .
. называется периодической,
если существует такое число
называется периодической,
если существует такое число 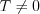 , при котором для всех
, при котором для всех  из области определения функции выполняется равенство
из области определения функции выполняется равенство 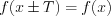 . Такое наименьшее число называется
основным периодом функции
.
. Такое наименьшее число называется
основным периодом функции
. Все тригонометрические функции
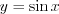 ,
, 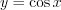 ,
, 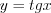 и
и 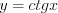 являются периодическими.
являются периодическими.Чтобы построить график периодической функции, достаточно построить ее график на основном (наименьшем) периоде
 и выполнить параллельный перенос этого графика вдоль оси абсцисс на любое количество периодов влево и вправо.
и выполнить параллельный перенос этого графика вдоль оси абсцисс на любое количество периодов влево и вправо. Функция
 обратима
, (имеет обратную функцию), если она или монотонно возрастает или монотонно убывает на всей своей области определения.
обратима
, (имеет обратную функцию), если она или монотонно возрастает или монотонно убывает на всей своей области определения. Функция
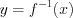 называется
обратной
к функции
называется
обратной
к функции  , если в каждой точке
, если в каждой точке  области значений обратимой функции
области значений обратимой функции 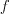 она принимает такое значение
она принимает такое значение  , что
, что 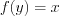 .
. Функции
 и
и 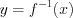 образуют пару взаимно обратных функций. Взаимно обратные функции обладают следующими
свойствами
:
образуют пару взаимно обратных функций. Взаимно обратные функции обладают следующими
свойствами
: 1) область определения функции
 является областью значений функции
является областью значений функции 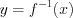 , а область значений функции
, а область значений функции  является областью определения функции
является областью определения функции 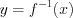 , т.е.
, т.е. 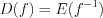 ,
, 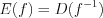 ;
; 2) если функция
 монотонно возрастает (убывает), то и функция
монотонно возрастает (убывает), то и функция 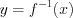 возрастает (убывает);
возрастает (убывает); 3) графики взаимно обратных функций симметричны относительно прямой
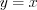 .
.Например, функции 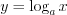 и
и 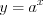 (рис. 2.6) взаимно обратные.
(рис. 2.6) взаимно обратные.
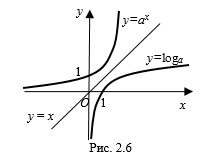
Чтобы найти функцию обратную функции  необходимо решить уравнение относительно переменной
необходимо решить уравнение относительно переменной  и в этом уравнении заменить
и в этом уравнении заменить  на
на  , а
, а  заменить на
заменить на  .
.
Пример 1.
Найдите количество всех целых чисел из области значений функции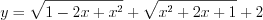 , которые она принимает на промежутке
, которые она принимает на промежутке 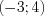 .
.
Решение
. Запишем функцию в виде 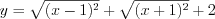 , откуда
, откуда 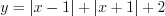 .
.
1. Найдем нули функций, записанных под знаками модулей, решая уравнения 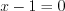 , откуда
, откуда  и
и 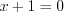 , откуда
, откуда 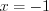 .
.
2. Нанесем числа  и
и  на интервал
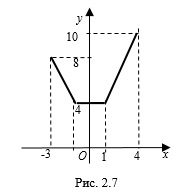
на интервал 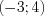 (рис. 2.7) и раскроем модули на полученных промежутках:
(рис. 2.7) и раскроем модули на полученных промежутках:
1) если ![x\in (-3;-1] LaTeX formula: x\in (-3;-1]](/uploads/formulas/0604634a849d375ffcb580e5822f524c1723922f.1.1.png) , то
, то 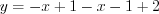 или
или 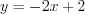 ;
;
![x\in (-1;1] LaTeX formula: x\in (-1;1]](/uploads/formulas/ca151a2ac9be1e4eda7d46485d63967e21e265fa.1.1.png) , то
, то 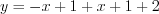 или
или 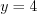 ;
; 3) если
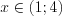 , то
, то 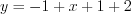 или
или 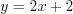 .
. 3. Построим графики полученных функций на соответствующих промежутках (рис. 2.7). Запишем область значений функции на промежутке
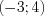 :
: 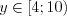 . Промежутку
. Промежутку 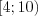 принадлежит шесть целых чисел:
принадлежит шесть целых чисел:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Ответ:
 .
.
![f(x)=15\left | x \right |^{51}+\sqrt[3]{x}-\frac{16}{x}+\cos x+\log_{5}\left | x \right | LaTeX formula: f(x)=15\left | x \right |^{51}+\sqrt[3]{x}-\frac{16}{x}+\cos x+\log_{5}\left | x \right |](/uploads/formulas/7bc640c17ab15a6a281b3ce0b9a77864d60fe83d.1.1.png) , а ось ординат является для него серединным перпендикуляром.
, а ось ординат является для него серединным перпендикуляром. Решение . Рассмотрим отрезок
 , который пересекает ось ординат в точке
, который пересекает ось ординат в точке 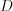 , а концы его лежат на графике функции
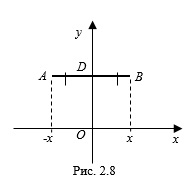
, а концы его лежат на графике функции ![f(x)=15\left | x \right |^{51}+\sqrt[3]{x}-\frac{16}{x}+\cos x+\log_{5}\left | x \right | LaTeX formula: f(x)=15\left | x \right |^{51}+\sqrt[3]{x}-\frac{16}{x}+\cos x+\log_{5}\left | x \right |](/uploads/formulas/7bc640c17ab15a6a281b3ce0b9a77864d60fe83d.1.1.png) (рис. 2.8).
(рис. 2.8). Так как ось ординат является серединным перпендикуляром отрезка
 , то
, то 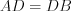 и
и 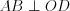 . В таком случае справедливо равенство
. В таком случае справедливо равенство 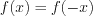 .
.
![15\left | x \right |^{51}+\sqrt[3]{x}-\frac{16}{x}+\cos x+\ log_{5}\left | x \right |=15\left | x \right |^{51}-\sqrt[3]{x}+\frac{16}{x}+\cos x+\ log_{5}\left | x \right | LaTeX formula: 15\left | x \right |^{51}+\sqrt[3]{x}-\frac{16}{x}+\cos x+\ log_{5}\left | x \right |=15\left | x \right |^{51}-\sqrt[3]{x}+\frac{16}{x}+\cos x+\ log_{5}\left | x \right |](/uploads/formulas/275143e273ba7efa5e7efa9deb7027314851d853.1.1.png)
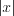 .
.Упростим полученное уравнение и найдем значение
 :
: ![\sqrt[3]{x}-\frac{16}{x}=-\sqrt[3]{x}+\frac{16}{x} LaTeX formula: \sqrt[3]{x}-\frac{16}{x}=-\sqrt[3]{x}+\frac{16}{x}](/uploads/formulas/a83b2aa7f2bcfeea8f2cd9ade5de25a87bca174e.1.1.png) ,
, ![2\sqrt[3]{x}=\frac{2\cdot 16}{x} LaTeX formula: 2\sqrt[3]{x}=\frac{2\cdot 16}{x}](/uploads/formulas/1a33a540459ecc9d171dc6df704d7c9ae22bcebe.1.1.png) ,
, ![\sqrt[3]{x}=\frac{ 16}{x} LaTeX formula: \sqrt[3]{x}=\frac{ 16}{x}](/uploads/formulas/95ea42fda43d4e2b9c6c386080d4a0e4818bd278.1.1.png) ,
, 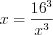 ,
, 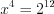 ,
, 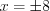
Найдем длину отрезка
 :
: 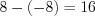 .
.Ответ:
 .
. и
и  , является функцией.
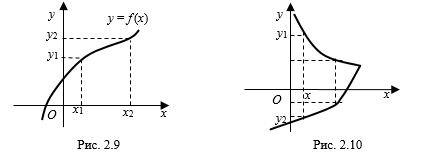
, является функцией. Например, на рисунке 2.9 изображен график некоторой функции (каждому значению соответствует единственное значение
соответствует единственное значение  ). На рисунке 2.10 изображена линия, которая не является графиком никакой функции (показано, что одному значению
). На рисунке 2.10 изображена линия, которая не является графиком никакой функции (показано, что одному значению  соответствуют два значения
соответствуют два значения  ).
).