Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты


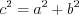 , (8.3)
, (8.3) , (8.12)
, (8.12)
Четырехугольником называют многоугольник, имеющий четыре вершины. Среди всех четырехугольников выделяют параллелограмм, ромб, прямоугольник, квадрат и трапецию. 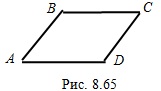
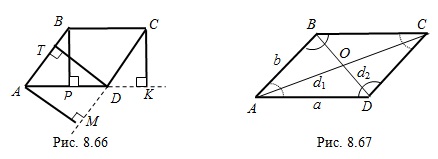
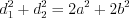 , (8.15)
, (8.15)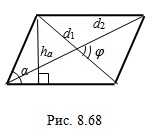
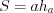 ; (8.16)
; (8.16) ; (8.17)
; (8.17)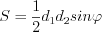 . (8.18)
. (8.18)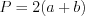 . (8.19)
. (8.19)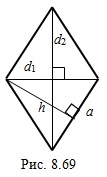
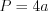 . (8.20)
. (8.20)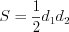 . (8.21)
. (8.21)
 ; (8.22)
; (8.22)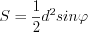 . (8.23)
. (8.23)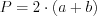 . (8.24)
. (8.24)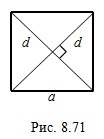
 (8.25)
(8.25) . (8.26)
. (8.26)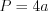 . (8.27)
. (8.27)
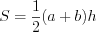 ;(8.28)
;(8.28)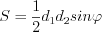 . (8.29)
. (8.29)
Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.
Например, на рисунке 8.65 изображен параллелограмм  , у которого сторона
, у которого сторона  параллельна стороне
параллельна стороне 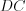 , а сторона
, а сторона  параллельна стороне
параллельна стороне  .
.
 , у которого сторона
, у которого сторона  параллельна стороне
параллельна стороне 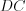 , а сторона
, а сторона  параллельна стороне
параллельна стороне  .
.
Высотой параллелограмма называют отрезок перпендикуляра, заключенный между его параллельными сторонами или отрезок перпендикуляра, проведенного из вершины параллелограмма на прямую, содержащую противолежащую сторону.
Например, на рисунке 8.66 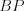 – высота, проведенная к стороне
– высота, проведенная к стороне  ,
, 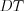 – высота, проведенная к стороне
– высота, проведенная к стороне  ,
, 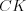 – высота, проведенная из вершины
– высота, проведенная из вершины  на прямую, содержащую сторону
на прямую, содержащую сторону  , а
, а 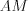 – высота, проведенная из вершины
– высота, проведенная из вершины  на прямую, содержащую сторону
на прямую, содержащую сторону 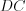 .
.
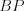 – высота, проведенная к стороне
– высота, проведенная к стороне  ,
, 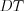 – высота, проведенная к стороне
– высота, проведенная к стороне  ,
, 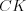 – высота, проведенная из вершины
– высота, проведенная из вершины  на прямую, содержащую сторону
на прямую, содержащую сторону  , а
, а 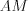 – высота, проведенная из вершины
– высота, проведенная из вершины  на прямую, содержащую сторону
на прямую, содержащую сторону 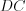 .
.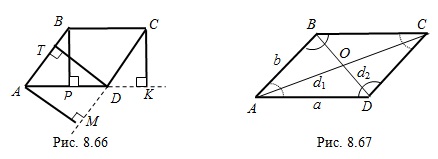
Свойства параллелограмма
1. Противолежащие стороны параллелограмма равны.
Например, на рисунке 8.67 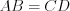 и
и 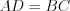 .
.
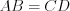 и
и 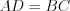 .
.2. Противолежащие углы параллелограмма равны.
Например, на рисунке 8.67 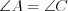 и
и 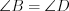 .
.
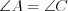 и
и 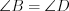 .
.3. Диагонали параллелограмма делятся точкой пересечения пополам.
Например, на рисунке 8.67 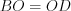 и
и 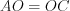 .
.
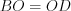 и
и 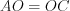 .
.4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов длин всех его сторон:
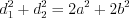 , (8.15)
, (8.15)где  и
и  – смежные стороны,
– смежные стороны,  и
и 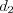 – диагонали параллелограмма.
– диагонали параллелограмма.
 и
и  – смежные стороны,
– смежные стороны,  и
и 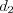 – диагонали параллелограмма.
– диагонали параллелограмма. 5. Сумма углов параллелограмма, прилежащих к одной стороне, равна  .
.
 .
. Например, на рисунке 8.67 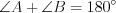 .
.
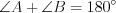 .
.Признаки параллелограмма
1. Если у выпуклого четырехугольника две противолежащие стороны параллельны и равны, то этот четырехугольник – параллелограмм.
2. Если у выпуклого четырехугольника противолежащие стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если у выпуклого четырехугольника противолежащие углы попарно равны, то этот четырехугольник – параллелограмм.
4. Если у выпуклого четырехугольника диагонали точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Рассмотрим параллелограмм, у которого:  и
и  – смежные стороны,
– смежные стороны, 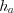 – высота, проведенная к стороне
– высота, проведенная к стороне  ,
,  – острый угол,
– острый угол,  и
и 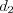 – диагонали,
– диагонали, 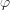 – угол между диагоналями (рис. 8.68).
– угол между диагоналями (рис. 8.68).
 и
и  – смежные стороны,
– смежные стороны, 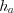 – высота, проведенная к стороне
– высота, проведенная к стороне  ,
,  – острый угол,
– острый угол,  и
и 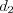 – диагонали,
– диагонали, 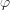 – угол между диагоналями (рис. 8.68).
– угол между диагоналями (рис. 8.68).
Площадь параллелограмма можно вычислить по одной из формул:
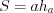 ; (8.16)
; (8.16) ; (8.17)
; (8.17)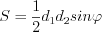 . (8.18)
. (8.18)Периметр параллелограмма можно вычислить по формуле:
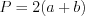 . (8.19)
. (8.19)Ромбом называют параллелограмм, все стороны которого равны.
Например, на рисунке 8.69 изображен ромб:  – сторона,
– сторона,  – высота,
– высота,  ,
, 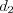 его диагонали.
его диагонали.
 – сторона,
– сторона,  – высота,
– высота,  ,
, 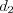 его диагонали.
его диагонали.
Свойства ромба
Ромбу присущи все свойства параллелограмма и, кроме того, свойства:
1) диагонали ромба взаимно перпендикулярны;
2) диагонали ромба являются биссектрисами его внутренних углов.
Признаки ромба
1. Параллелограмм является ромбом, если две его смежные стороны равны.
2. Параллелограмм является ромбом, если его диагонали перпендикулярны.
3. Параллелограмм является ромбом, если одна из диагоналей является биссектрисой его угла.
Периметр ромба можно вычислить по формуле:
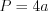 . (8.20)
. (8.20)Площадь ромба можно вычислить по тем же формулам, что и площадь параллелограмма, кроме того, и по формуле:
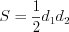 . (8.21)
. (8.21)Прямоугольником называют параллелограмм, у которого все углы прямые.
Например, на рисунке 8.70 изображен прямоугольник, у которого  и
и  – смежные стороны,
– смежные стороны, 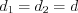 – диагонали, φ – угол между диагоналями.
– диагонали, φ – угол между диагоналями.
 и
и  – смежные стороны,
– смежные стороны, 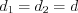 – диагонали, φ – угол между диагоналями.
– диагонали, φ – угол между диагоналями. 
Свойства прямоугольника
Прямоугольнику присущи все свойства параллелограмма. Кроме того диагонали прямоугольника равны.
Признаки прямоугольника
1. Параллелограмм является прямоугольником, если его диагонали равны.
2. Параллелограмм является прямоугольником, если один из его углов прямой.
3. Четырехугольник является прямоугольником, если три его угла прямые.
Площадь прямоугольника можно вычислить по формулам:
 ; (8.22)
; (8.22)или
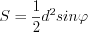 . (8.23)
. (8.23)Периметр прямоугольника можно вычислить по формуле:
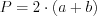 . (8.24)
. (8.24)Квадратом называют прямоугольник, у которого все стороны равны.

Например, на рисунке 8.71 изображен квадрат со стороной  и диагональю
и диагональю  .
.
 и диагональю
и диагональю  .
.Квадрат обладает всеми свойствами параллелограмма, ромба и прямоугольника.
Признаки квадрата
1. Прямоугольник является квадратом, если две его смежные стороны равны.
2. Прямоугольник является квадратом, если его диагонали перпендикулярны.
3. Прямоугольник является квадратом, если одна из диагоналей является биссектрисой его угла.
Площадь квадрата можно вычислить по формулам:
 (8.25)
(8.25)или
 . (8.26)
. (8.26)Периметр квадрата можно вычислить по формуле:
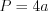 . (8.27)
. (8.27)Трапецией называют четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные – боковыми сторонами.
Например, на рисунках 8.72 – 8.74 изображены трапеции  . Отрезки
. Отрезки  и
и  – основания, а
– основания, а  и
и 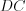 – боковые стороны трапеций.
– боковые стороны трапеций.
 . Отрезки
. Отрезки  и
и  – основания, а
– основания, а  и
и 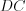 – боковые стороны трапеций.
– боковые стороны трапеций.
Трапецию называют равнобедренной (равнобокой), если ее боковые стороны равны.
Например, на рисунке 8.72 изображена равнобедренная трапеция, а на рисунке 8.73 – неравнобедренная.
Трапецию называют прямоугольной, если ее боковая сторона перпендикулярна основаниям.
Например, на рисунке 8.74 изображена прямоугольная трапеция.
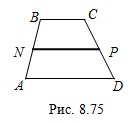
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Например, на рисунке 8.75 отрезок 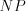 – средняя линия трапеции
– средняя линия трапеции  .
.
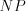 – средняя линия трапеции
– средняя линия трапеции  .
.
Свойства средней линии трапеции
1. Средняя линия трапеции параллельна основаниям трапеции.
2. Средняя линия трапеции равна полусумме ее оснований.
Например, на рисунке 8.75 отрезок 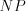 – средняя линия трапеции
– средняя линия трапеции  , следовательно,
, следовательно, 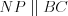 ,
, 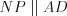 и
и 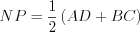 .
.
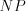 – средняя линия трапеции
– средняя линия трапеции  , следовательно,
, следовательно, 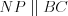 ,
, 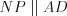 и
и 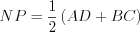 .
. Сумма углов трапеции, прилежащих к ее боковой стороне, равна  .
.
 .
. Например, на рисунках 4.8 – 4.10 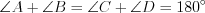 .
.
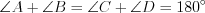 .
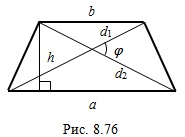
. Рассмотрим трапецию (рис. 8.76):  и
и  – основания,
– основания,  – высота,
– высота,  ,
, 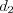 – диагонали, φ – угол между диагоналями.
– диагонали, φ – угол между диагоналями.
 и
и  – основания,
– основания,  – высота,
– высота,  ,
, 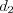 – диагонали, φ – угол между диагоналями.
– диагонали, φ – угол между диагоналями. 
Признак трапеции: четырехугольник является трапецией, если две его параллельные стороны не равны.
Площадь трапеции можно вычислить по формулам:
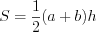 ;(8.28)
;(8.28)или
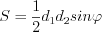 . (8.29)
. (8.29)Пример 1. Дан выпуклый четырехугольник  , у которого диагональ равна 8,
, у которого диагональ равна 8, 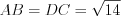 ,
, 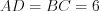 . Найдите другую диагональ этого четырехугольника.
. Найдите другую диагональ этого четырехугольника.
 , у которого диагональ равна 8,
, у которого диагональ равна 8, 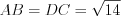 ,
, 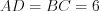 . Найдите другую диагональ этого четырехугольника.
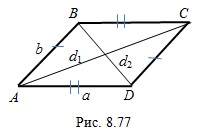
. Найдите другую диагональ этого четырехугольника. Решение. Так как противолежащие стороны данного четырехугольника попарно равны, то этот четырехугольник – параллелограмм (рис. 8.77).

Ответ: 6.
Пример 2. Стороны параллелограмма  и
и  относятся как
относятся как 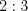 и образуют угол
и образуют угол  , а его периметр равен 30. Найдите площадь параллелограмма.
, а его периметр равен 30. Найдите площадь параллелограмма.
 и
и  относятся как
относятся как 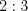 и образуют угол
и образуют угол  , а его периметр равен 30. Найдите площадь параллелограмма.
, а его периметр равен 30. Найдите площадь параллелограмма. Площадь параллелограмма найдем по формуле 8.17. Получим: 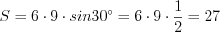 .
.
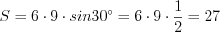 .
.Ответ: 27.
Пример 3. Дан параллелограмм, диагонали которого перпендикулярны и равны 12 и 16. Найдите его высоту.
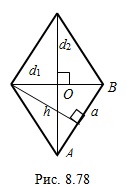
Решение. Так как диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб (рис. 8.78).

Так как диагонали ромба точкой пересечения делятся пополам, то 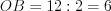 , а
, а 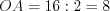 .
.
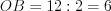 , а
, а 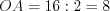 .
.Ответ: 9,6.
Пример 4. Дан четырехугольник, у которого диагонали равны 10 см и в точке пересечения делятся пополам. Найдите периметр этого четырехугольника, если известно, что угол между диагоналями равен  .
.
 .
.Решение. Так как диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник параллелограмм, а так как его диагонали равны, то имеем прямоугольник (рис. 8.79).

Рассмотрим равнобедренный треугольник 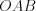 . Поскольку
. Поскольку 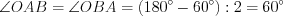 , то
, то  см.
см.
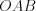 . Поскольку
. Поскольку 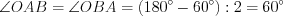 , то
, то  см.
см. Ответ: 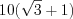 см.
см.
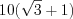 см.
см.Пример 5. Периметр правильного четырехугольника равен 12. Найдите его диагональ.
Решение. Так как четырехугольник правильный, то он квадрат. С учетом формулы 8.27, найдем сторону квадрата:  .
.
 .
. Ответ: 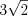 .
.
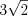 .
. Пример 6. Дан четырехугольник, у которого диагонали образуют угол 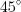 и равны соответственно 3 и 4, а сумма двух неравных параллельных сторон равна 6. Найдите высоту этого четырехугольника.
и равны соответственно 3 и 4, а сумма двух неравных параллельных сторон равна 6. Найдите высоту этого четырехугольника.
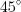 и равны соответственно 3 и 4, а сумма двух неравных параллельных сторон равна 6. Найдите высоту этого четырехугольника.
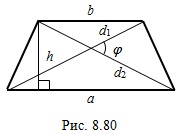
и равны соответственно 3 и 4, а сумма двух неравных параллельных сторон равна 6. Найдите высоту этого четырехугольника.Решение. Так как две параллельные стороны четырехугольника не равны, то этот четырехугольник – трапеция (рис. 8.80).

Ответ: 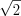 .
.
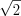 .
. Пример 7. Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 2, периметр равен 23. Найдите площадь трапеции.
Решение. Рассмотрим трапецию  (рис. 8.81) и проведем ее диагональ
(рис. 8.81) и проведем ее диагональ 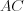 . Углы 1 и 3 равны как накрест лежащие при параллельных прямых
. Углы 1 и 3 равны как накрест лежащие при параллельных прямых  и
и  с секущей
с секущей 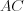 . Так как диагональ
. Так как диагональ 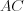 является биссектрисой угла
является биссектрисой угла 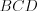 , то
, то 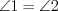 .
.
 (рис. 8.81) и проведем ее диагональ
(рис. 8.81) и проведем ее диагональ 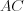 . Углы 1 и 3 равны как накрест лежащие при параллельных прямых
. Углы 1 и 3 равны как накрест лежащие при параллельных прямых  и
и  с секущей
с секущей 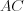 . Так как диагональ
. Так как диагональ 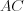 является биссектрисой угла
является биссектрисой угла 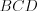 , то
, то 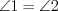 .
. 
В таком случае треугольник 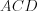 равнобедренный с боковыми сторонами
равнобедренный с боковыми сторонами  и
и  .
.
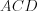 равнобедренный с боковыми сторонами
равнобедренный с боковыми сторонами  и
и  .
.Пусть  . Согласно условию задачи
. Согласно условию задачи 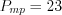 и
и 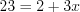 , откуда
, откуда 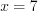 . Так как
. Так как 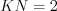 , то
, то 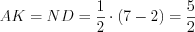 .
.
 . Согласно условию задачи
. Согласно условию задачи 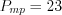 и
и 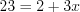 , откуда
, откуда 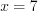 . Так как
. Так как 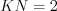 , то
, то 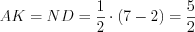 .
.Ответ: 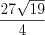 .
.
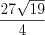 .
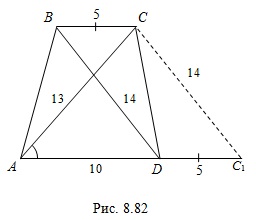
.Пример 8. В трапеции длины оснований равны 5 и 10, а длины диагоналей равны 13 и 14. Найдите площадь трапеции.
Решение. Рассмотрим трапецию  (рис. 8.82). На продолжении стороны
(рис. 8.82). На продолжении стороны  отложим отрезок
отложим отрезок 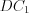 , равный отрезку
, равный отрезку  . Тогда имеем параллелограмм
. Тогда имеем параллелограмм 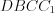 , так как
, так как 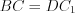 и
и 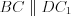 . Значит,
. Значит, 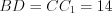 . Так как
. Так как  , то
, то  .
.
 (рис. 8.82). На продолжении стороны
(рис. 8.82). На продолжении стороны  отложим отрезок
отложим отрезок 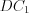 , равный отрезку
, равный отрезку  . Тогда имеем параллелограмм
. Тогда имеем параллелограмм 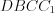 , так как
, так как 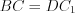 и
и 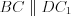 . Значит,
. Значит, 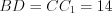 . Так как
. Так как  , то
, то  .
. 
Получим: 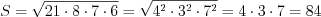 .
.
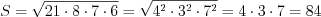 .
.Ответ: 84.
1. Существует несколько формул для нахождения площади каждого из четырехугольников. Выбирая формулу, учитывайте данные задачи.
2. Теорема Пифагора: квадрат гипотенузы треугольника равен сумме квадратов его катетов:
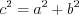 , (8.3)
, (8.3)где  – гипотенуза,
– гипотенуза,  и
и  – катеты.
– катеты.
 – гипотенуза,
– гипотенуза,  и
и  – катеты.
– катеты.3. Формула Герона:
 , (8.12)
, (8.12)где  – стороны,
– стороны, 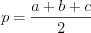 – полупериметр треугольника
– полупериметр треугольника
 – стороны,
– стороны, 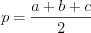 – полупериметр треугольника
– полупериметр треугольника

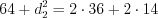
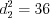 ,
, 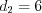
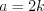
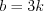 , то
, то 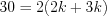
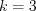 . Тогда
. Тогда 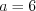
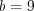 .
.
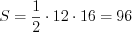

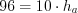
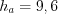

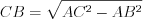
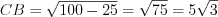

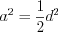 ,
, 
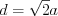 ,
, 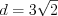
 .
.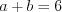
 , откуда
, откуда 
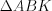
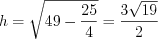
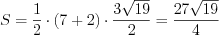
 найдем по формуле Герона
найдем по формуле Герона 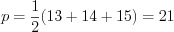 .
.