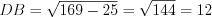Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты

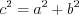 , (8.3)
, (8.3)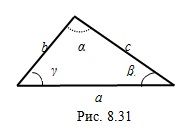
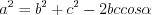 , (8.4)
, (8.4)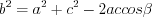 , (8.4.1)
, (8.4.1)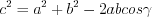 . (8.4.2)
. (8.4.2)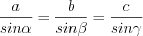 (8.5)
(8.5)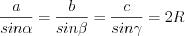 , (8.5.1)
, (8.5.1)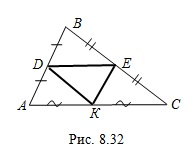

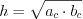 , (8.6)
, (8.6)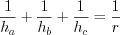 . (8.7)
. (8.7)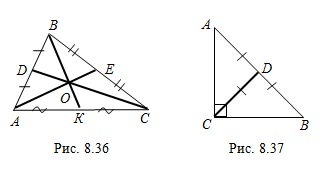
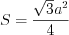 , (8.8)
, (8.8)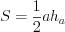 , (8.9)
, (8.9)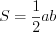 , (8.10)
, (8.10)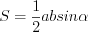 , (8.11)
, (8.11) , (8.12)
, (8.12)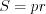 , (8.13)
, (8.13)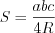 , (8.14)
, (8.14)

Треугольником называют многоугольник, имеющий три вершины (рис. 8.27 – 8.29).

Классификация треугольников по сторонам
1. Если все три стороны треугольника равны, то треугольник равносторонний. Все внутренние углы равностороннего треугольника равны.
Например, на рисунке 8.27 изображен равносторонний треугольник  :
: 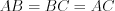 ;
; 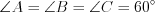 .
.
 :
: 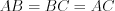 ;
; 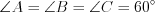 .
.2. Если две стороны треугольника равны, то треугольник равнобедренный. Стороны, имеющие одинаковую длину, называют боковыми сторонами, а третью сторону – основанием этого треугольника. Углы при основании равнобедренного треугольника равны.
Например, на рисунке 8.28 изображен равнобедренный треугольник 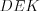 с боковыми сторонами
с боковыми сторонами 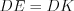 и основанием
и основанием 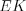 , а
, а 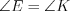 .
.
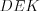 с боковыми сторонами
с боковыми сторонами 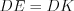 и основанием
и основанием 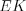 , а
, а 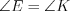 .
.3. Если все стороны треугольника имеют различную длину, то треугольник разносторонний (произвольный).
Например, на рисунке 8.29 изображен разносторонний треугольник 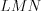 .
.
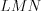 .
. Длина стороны треугольника меньше суммы длин двух других его сторон, причем, большая сторона треугольника лежит против большего его угла.
Например: 1) если на рисунке 8.27 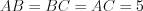 , то
, то 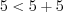 ; 2) если на рисунке 8.28
; 2) если на рисунке 8.28 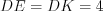 , то длина стороны
, то длина стороны 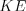 меньше 8, но больше 4.
меньше 8, но больше 4.
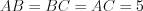 , то
, то 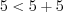 ; 2) если на рисунке 8.28
; 2) если на рисунке 8.28 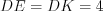 , то длина стороны
, то длина стороны 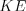 меньше 8, но больше 4.
меньше 8, но больше 4. Классификация треугольников по углам
1. Если все углы треугольника острые, то треугольник остроугольный (на рисунке 8.27 треугольник  ).
).
 ).
).2. Если один из углов треугольника тупой, то треугольник тупоугольный (на рисунке 8.28 треугольник 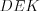 ).
).
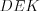 ).
).3. Если один из углов треугольника прямой, то треугольник прямоугольный. Сторону прямоугольного треугольника, лежащую против прямого угла, называют гипотенузой, две другие стороны – катетами. Например, на рисунке 8.29 треугольник 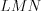 – прямоугольный, отрезок
– прямоугольный, отрезок 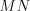 – гипотенуза этого треугольника, а отрезки
– гипотенуза этого треугольника, а отрезки 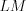 и
и 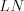 – его катеты.
– его катеты.
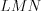 – прямоугольный, отрезок
– прямоугольный, отрезок 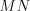 – гипотенуза этого треугольника, а отрезки
– гипотенуза этого треугольника, а отрезки 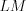 и
и 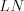 – его катеты.
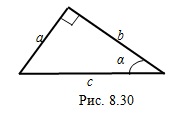
– его катеты.Рассмотрим прямоугольный треугольник, у которого  и
и  – катеты,
– катеты,  – гипотенуза,
– гипотенуза,  – острый угол (рис. 8.30).
– острый угол (рис. 8.30).
 и
и  – катеты,
– катеты,  – гипотенуза,
– гипотенуза,  – острый угол (рис. 8.30).
– острый угол (рис. 8.30).
Теорема Пифагора: квадрат гипотенузы треугольника равен сумме квадратов его катетов:
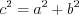 , (8.3)
, (8.3)где  – гипотенуза,
– гипотенуза,  и
и  – катеты.
– катеты.
 – гипотенуза,
– гипотенуза,  и
и  – катеты.
– катеты.Например, если катеты треугольника соответственно равны 3 и 4, то гипотенуза этого треугольника равна 5. Такой треугольник называют египетским.
Соотношения между сторонами и углами в прямоугольном треугольнике
1. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
2. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
3. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему катету.
Например, на рисунке 8.30: 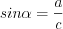 ;
; 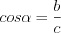 ;
; 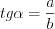 .
.
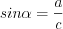 ;
; 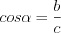 ;
; 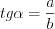 .
. Катет, лежащий против угла  , равен половине гипотенузы.
, равен половине гипотенузы.
 , равен половине гипотенузы.
, равен половине гипотенузы. Рассмотрим произвольный треугольник, у которого  – стороны,
– стороны, 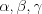 – соответственно противолежащие им углы (рис. 8.31).
– соответственно противолежащие им углы (рис. 8.31).
 – стороны,
– стороны, 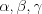 – соответственно противолежащие им углы (рис. 8.31).
– соответственно противолежащие им углы (рис. 8.31).
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих же сторон на косинус угла между ними:
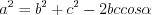 , (8.4)
, (8.4)или
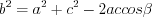 , (8.4.1)
, (8.4.1)или
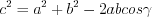 . (8.4.2)
. (8.4.2)Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих им углов:
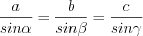 (8.5)
(8.5)или
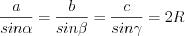 , (8.5.1)
, (8.5.1)где  – радиус окружности, описанной около этого треугольника.
– радиус окружности, описанной около этого треугольника.
 – радиус окружности, описанной около этого треугольника.
– радиус окружности, описанной около этого треугольника.Линии в треугольнике
Среди всех линий, которые можно провести в треугольнике выделяют среднюю линию треугольника, биссектрису треугольника, его медиану и высоту.
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Свойства средней линии треугольника
1. Средняя линия треугольника равна половине длины его третьей стороны.
2. Средняя линия треугольника параллельна одной из сторон треугольника.
Например, если отрезки 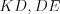 и
и 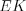 – средние линии треугольника
– средние линии треугольника  (рис. 8.32) и длины их соответственно равны 8, 9 и 7, то стороны
(рис. 8.32) и длины их соответственно равны 8, 9 и 7, то стороны 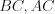 и
и  этого треугольника соответственно равны 16, 18 и 14.
этого треугольника соответственно равны 16, 18 и 14.
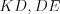 и
и 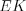 – средние линии треугольника
– средние линии треугольника  (рис. 8.32) и длины их соответственно равны 8, 9 и 7, то стороны
(рис. 8.32) и длины их соответственно равны 8, 9 и 7, то стороны 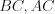 и
и  этого треугольника соответственно равны 16, 18 и 14.
этого треугольника соответственно равны 16, 18 и 14.
Высотой треугольника называют перпендикуляр, проведенный из вершины треугольника на прямую, содержащую противолежащую сторону.
Например, на рисунке 8.33 изображены высоты остроугольного треугольника  : отрезки
: отрезки 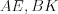 и
и  .
.
 : отрезки
: отрезки 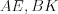 и
и  .
.На рисунке 8.34 изображена одна из высот тупоугольного треугольника 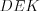 : высота
: высота 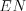 .
.
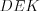 : высота
: высота 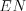 .
.На рисунке 8.35 изображены три высоты прямоугольного треугольника 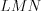 : высоты
: высоты 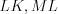 и
и 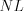 .
.
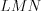 : высоты
: высоты 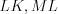 и
и 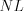 .
.
Свойства высоты треугольника
1. В остроугольном и прямоугольном треугольнике три высоты треугольника пересекаются в одной точке (точка  на рисунке 8.33 и точка
на рисунке 8.33 и точка 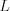 на рисунке 8.35).
на рисунке 8.35).
 на рисунке 8.33 и точка
на рисунке 8.33 и точка 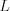 на рисунке 8.35).
на рисунке 8.35). 2. Если высота треугольника проведена из вершины прямого угла к гипотенузе, то она является средним геометрическим проекций катетов на гипотенузу (рис. 8.5):
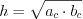 , (8.6)
, (8.6)где  и
и 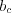 – проекции катетов на гипотенузу.
– проекции катетов на гипотенузу.
 и
и 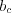 – проекции катетов на гипотенузу.
– проекции катетов на гипотенузу.3. Для всякого треугольника зависимость между его высотами 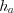 ,
, 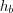 ,
, 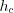 и радиусом вписанной окружности r выражается формулой:
и радиусом вписанной окружности r выражается формулой:
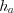 ,
, 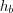 ,
, 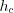 и радиусом вписанной окружности r выражается формулой:
и радиусом вписанной окружности r выражается формулой: 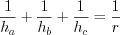 . (8.7)
. (8.7)Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Например, на рисунке 8.36 изображены медианы треугольника  : отрезки
: отрезки 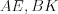 и
и  .
.
 : отрезки
: отрезки 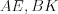 и
и  .
.
Свойства медианы треугольника
1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 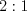 , считая от вершины.
, считая от вершины.
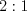 , считая от вершины.
, считая от вершины. Например, на рисунке 8.36 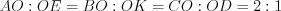 .
.
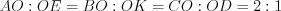 .
.2. Медиана делит треугольник на два равновеликих треугольника (треугольники, имеющие равные площади, называют равновеликими).
Например, на рисунке 8.36 треугольники 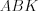 и
и 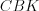 равновеликие.
равновеликие.
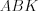 и
и 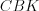 равновеликие.
равновеликие. 3. Если медиана проведена к гипотенузе прямоугольного треугольника, то она равна половине гипотенузы.
Например, на рисунке 8.37 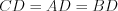 .
.
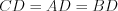 .
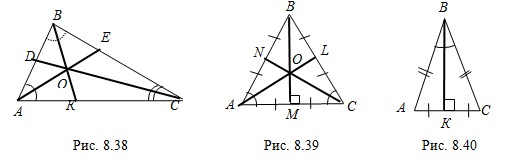
. Биссектрисой треугольника называют отрезок биссектрисы внутреннего угла треугольника, заключенный между вершиной треугольника и точкой пересечения биссектрисы угла и стороны треугольника.
Например, на рисунке 8.38 отрезки 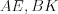 и
и  – биссектрисы внутренних углов треугольника
– биссектрисы внутренних углов треугольника  .
.
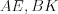 и
и  – биссектрисы внутренних углов треугольника
– биссектрисы внутренних углов треугольника  .
.
Свойства биссектрисы треугольника
1. Три биссектрисы треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник.
Например, точка  на рисунке 8.38.
на рисунке 8.38.
 на рисунке 8.38.
на рисунке 8.38.2. В равностороннем треугольнике все биссектрисы равны и являются высотами и медианами этого треугольника.
Например, на рисунке 8.39 биссектрисы 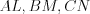 – высоты и медианы правильного треугольника
– высоты и медианы правильного треугольника  и
и 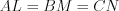 .
.
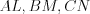 – высоты и медианы правильного треугольника
– высоты и медианы правильного треугольника  и
и 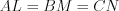 .
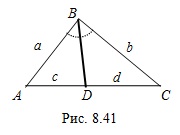
.3. Если биссектриса проведена из вершины равнобедренного треугольника к его основанию, то она является высотой и медианой этого треугольника.
Например, на рисунке 8.40 биссектриса  – высота и медиана равнобедренного треугольника
– высота и медиана равнобедренного треугольника  .
.
 – высота и медиана равнобедренного треугольника
– высота и медиана равнобедренного треугольника  .
.4. Биссектриса треугольника делит сторону этого треугольника на отрезки, пропорциональные прилежащим к ним сторонам.
Например, если 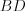 – биссектриса треугольника
– биссектриса треугольника  , изображенного на рисунке 8.41, то
, изображенного на рисунке 8.41, то 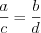 .
.
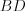 – биссектриса треугольника
– биссектриса треугольника  , изображенного на рисунке 8.41, то
, изображенного на рисунке 8.41, то 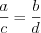 .
.
Формулы для вычисления площади треугольника
Для вычисления площади треугольника можно применять одну из следующих формул:
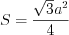 , (8.8)
, (8.8)где  – сторона равностороннего треугольника;
– сторона равностороннего треугольника;
 – сторона равностороннего треугольника;
– сторона равностороннего треугольника; 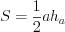 , (8.9)
, (8.9)где  – сторона,
– сторона, 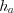 – высота, проведенная к стороне
– высота, проведенная к стороне  произвольного треугольника;
произвольного треугольника;
 – сторона,
– сторона, 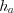 – высота, проведенная к стороне
– высота, проведенная к стороне  произвольного треугольника;
произвольного треугольника; 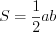 , (8.10)
, (8.10)где  и
и  – катеты прямоугольного треугольника;
– катеты прямоугольного треугольника;
 и
и  – катеты прямоугольного треугольника;
– катеты прямоугольного треугольника; 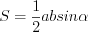 , (8.11)
, (8.11)где  и
и  – стороны,
– стороны,  – величина угла между ними произвольного треугольника;
– величина угла между ними произвольного треугольника;
 и
и  – стороны,
– стороны,  – величина угла между ними произвольного треугольника;
– величина угла между ними произвольного треугольника;Формула Герона:
 , (8.12)
, (8.12)где  – стороны,
– стороны, 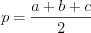 – полупериметр треугольника;
– полупериметр треугольника;
 – стороны,
– стороны, 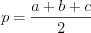 – полупериметр треугольника;
– полупериметр треугольника;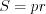 , (8.13)
, (8.13)где  - полупериметр треугольника,
- полупериметр треугольника,  - радиус окружности, вписанной в треугольник;
- радиус окружности, вписанной в треугольник;
 - полупериметр треугольника,
- полупериметр треугольника,  - радиус окружности, вписанной в треугольник;
- радиус окружности, вписанной в треугольник;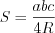 , (8.14)
, (8.14)где  – стороны,
– стороны,  – радиус окружности, описанной около треугольника.
– радиус окружности, описанной около треугольника.
 – стороны,
– стороны,  – радиус окружности, описанной около треугольника.
– радиус окружности, описанной около треугольника.Два треугольника равны, если все их соответственные стороны и углы равны.
Признаки равенства треугольников
1. Два треугольника равны, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника.
Например, на рисунке 8.42 треугольники 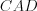 и
и 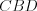 равны по двум сторонам и углу между ними.
равны по двум сторонам и углу между ними.
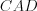 и
и 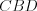 равны по двум сторонам и углу между ними.
равны по двум сторонам и углу между ними.2. Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника.
Например, на рисунке 8.43 треугольники 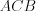 и
и 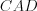 равны по стороне и прилежащим к ней углам.
равны по стороне и прилежащим к ней углам.
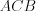 и
и 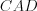 равны по стороне и прилежащим к ней углам.
равны по стороне и прилежащим к ней углам.3. Два треугольника равны, если три стороны одного треугольника соответственно равны трем сторонам другого треугольника.
Например, на рисунке 8.44 треугольники  и
и 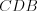 равны по трем сторонам.
равны по трем сторонам.
 и
и 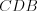 равны по трем сторонам.
равны по трем сторонам.
Признаки равенства прямоугольных треугольников
1. Прямоугольные треугольники равны, если катеты одного треугольника соответственно равны катетам другого треугольника.
Например, на рисунке 8.45 треугольники 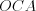 и
и  равны по двум катетам.
равны по двум катетам.
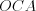 и
и  равны по двум катетам.
равны по двум катетам.2. Прямоугольные треугольники равны, если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника.
Например, на рисунке 8,46 треугольники 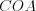 и
и 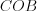 равны по катету и прилежащему острому углу.
равны по катету и прилежащему острому углу.
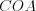 и
и 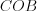 равны по катету и прилежащему острому углу.
равны по катету и прилежащему острому углу.3. Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника.
Например, на рисунке 8.47 треугольники 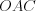 и
и 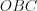 равны по гипотенузе и острому углу.
равны по гипотенузе и острому углу.
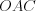 и
и 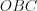 равны по гипотенузе и острому углу.
равны по гипотенузе и острому углу.4. Прямоугольные треугольники равны, если гипотенуза и катет одного треугольника соответствравны гипотенузе и катету другого треугольника.
Например, на рисунке 8.48 треугольники 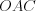 и
и 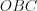 равны по гипотенузе и катету.
равны по гипотенузе и катету.
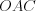 и
и 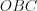 равны по гипотенузе и катету.
равны по гипотенузе и катету.
Два треугольника подобны, если все углы одного треугольника соответственно равны углам другого, а все стороны одного пропорциональны соответствующим (сходственным) сторонам другого треугольника.
Признаки подобия треугольников
1. Два треугольника подобны, если два угла одного треугольника равны двум углам другого.
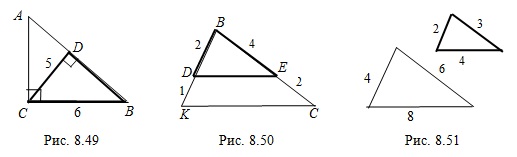
Например, на рисунке 8.49 треугольники 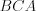 и
и 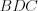 подобны (записывают
подобны (записывают 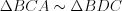 ), так как
), так как 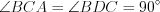 ,
, 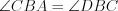 .
.
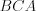 и
и 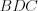 подобны (записывают
подобны (записывают 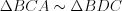 ), так как
), так как 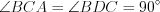 ,
, 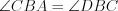 .
.2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, заключенные между ними, равны.
Например, на рисунке 8.50 треугольник 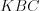 подобен треугольнику
подобен треугольнику 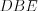 так как
так как 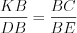 ,
, 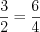 и угол
и угол  у них общий.
у них общий.
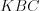 подобен треугольнику
подобен треугольнику 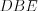 так как
так как 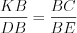 ,
, 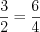 и угол
и угол  у них общий.
у них общий.3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого.
Например, на рисунке 8.51 изображены подобные треугольники, так как длины сторон одного из них в два раза больше длин сторон другого.

Отношение сходственных сторон подобных треугольников называют коэффициентом подобия  .
.
 .
. Отношение периметров подобных треугольников равно коэффициенту подобия  .
.
 .
. Отношение площадей подобных треугольников равно квадрату коэффициента подобия 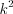 .
.
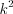 .
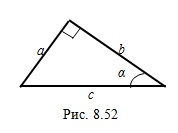
.Пример 1. Острый угол треугольника (рис. 8.52) 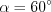 , а катет
, а катет  , лежащий против этого угла, равен
, лежащий против этого угла, равен 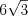 . Найдите гипотенузу
. Найдите гипотенузу  и катет
и катет  этого треугольника.
этого треугольника.
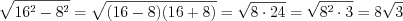 .
.

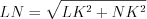 ,
, 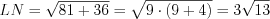 (см);
(см);

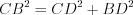 ,
, 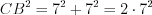 , а
, а  .
.



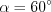 , а катет
, а катет  , лежащий против этого угла, равен
, лежащий против этого угла, равен 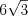 . Найдите гипотенузу
. Найдите гипотенузу  и катет
и катет  этого треугольника.
этого треугольника.

Решение. Согласно равенству 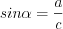 запишем:
запишем: 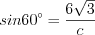 ,
, 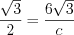 , откуда
, откуда 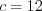 .
.
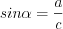 запишем:
запишем: 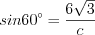 ,
, 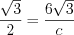 , откуда
, откуда 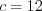 .
.А так как 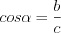 , то
, то 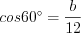 . Тогда
. Тогда 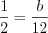 , откуда
, откуда 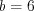 .
.
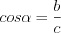 , то
, то 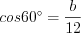 . Тогда
. Тогда 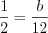 , откуда
, откуда 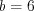 .
. Ответ: 12; 6.
Пример 2. Известно, что гипотенуза прямоугольного треугольника равна 16 и острый угол треугольника равен  . Найдите периметр этого треугольника.
. Найдите периметр этого треугольника.
 . Найдите периметр этого треугольника.
. Найдите периметр этого треугольника. Решение. Поскольку сумма углов треугольника равна  и один из его углов прямой, то острые углы этого треугольника равны
и один из его углов прямой, то острые углы этого треугольника равны  и
и  соответственно. Катет, лежащий против угла
соответственно. Катет, лежащий против угла  равен половине гипотенузы и равен 8.
равен половине гипотенузы и равен 8.
 и один из его углов прямой, то острые углы этого треугольника равны
и один из его углов прямой, то острые углы этого треугольника равны  и
и  соответственно. Катет, лежащий против угла
соответственно. Катет, лежащий против угла  равен половине гипотенузы и равен 8.
равен половине гипотенузы и равен 8.Из теоремы Пифагора 8.3 найдем другой катет этого треугольника:
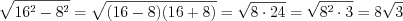 .
.Запишем периметр треугольника: 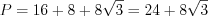 .
.
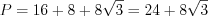 .
.Ответ: 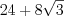 .
.
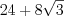 .
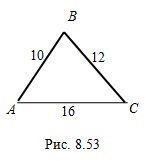
.Пример 3. Известно, что стороны треугольника  (рис. 8.53) равны 10 см, 12 см и 16 см. Выясните, является ли этот треугольник остроугольным.
(рис. 8.53) равны 10 см, 12 см и 16 см. Выясните, является ли этот треугольник остроугольным.
 (рис. 8.53) равны 10 см, 12 см и 16 см. Выясните, является ли этот треугольник остроугольным.
(рис. 8.53) равны 10 см, 12 см и 16 см. Выясните, является ли этот треугольник остроугольным.
Решение. Поскольку больший угол треугольника лежит против большей его стороны, то определим величину угла В.
Ответ: так как значение косинуса угла  отрицательное, то этот треугольник тупоугольный.
отрицательное, то этот треугольник тупоугольный.
 отрицательное, то этот треугольник тупоугольный.
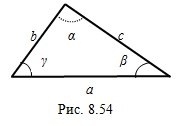
отрицательное, то этот треугольник тупоугольный. Пример 4. На рисунке 8.54 изображен треугольник, у которого сторона  равна
равна 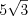 , сторона
, сторона  равна 5, а угол
равна 5, а угол  равен
равен  . Определите сторону
. Определите сторону  и величины углов
и величины углов  и
и 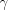 этого треугольника.
этого треугольника.
 равна
равна 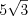 , сторона
, сторона  равна 5, а угол
равна 5, а угол  равен
равен  . Определите сторону
. Определите сторону  и величины углов
и величины углов  и
и 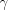 этого треугольника.
этого треугольника.
Решение. Согласно теореме синусов 8.5 запишем: 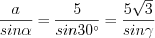 .
.
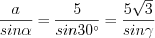 .
. Так как 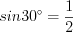 , то
, то 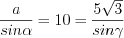 , откуда
, откуда 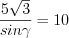 и
и 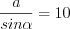 .
.
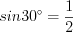 , то
, то 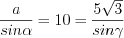 , откуда
, откуда 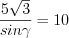 и
и 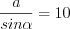 .
.Решая уравнение 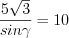 , получим:
, получим: 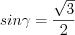 ,
, 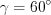 .
.
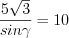 , получим:
, получим: 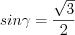 ,
, 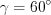 .
.Поскольку сумма внутренних углов треугольника равна  , то
, то 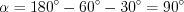 и
и 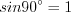 .
.
 , то
, то 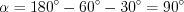 и
и 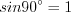 .
.Тогда, решая уравнение 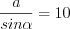 , получим:
, получим: 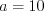 .
.
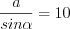 , получим:
, получим: 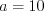 .
. Ответ: 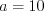 ,
, 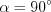 ,
, 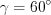 .
.
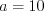 ,
, 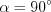 ,
, 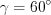 .
. Пример 5. В треугольнике 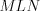 (рис. 8.55) высота
(рис. 8.55) высота 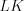 делит гипотенузу на отрезки
делит гипотенузу на отрезки 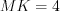 см и
см и 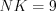 см. Найдите больший катет этого треугольника.
см. Найдите больший катет этого треугольника.
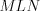 (рис. 8.55) высота
(рис. 8.55) высота 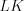 делит гипотенузу на отрезки
делит гипотенузу на отрезки 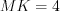 см и
см и 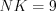 см. Найдите больший катет этого треугольника.
см. Найдите больший катет этого треугольника. 
По теореме Пифагора 8.3:
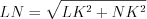 ,
, 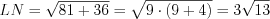 (см);
(см);Ответ: 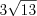 см.
см.
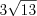 см.
см.Пример 6. Две высоты треугольника равны соответственно 5 и 6, а радиус окружности, вписанной в этот треугольник, равен 1. Найдите третью высоту треугольника.
Ответ: 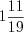 .
.
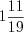 .
.Пример 7. В треугольнике  (рис. 8.56) точка
(рис. 8.56) точка  – точка пересечения медиан треугольника. Найдите медиану
– точка пересечения медиан треугольника. Найдите медиану  этого треугольника, зная, что
этого треугольника, зная, что 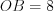 .
.
 (рис. 8.56) точка
(рис. 8.56) точка  – точка пересечения медиан треугольника. Найдите медиану
– точка пересечения медиан треугольника. Найдите медиану  этого треугольника, зная, что
этого треугольника, зная, что 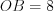 .
.
Решение. Так как точкой пересечения медианы треугольника делятся в отношении 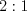 , считая от его вершины, то
, считая от его вершины, то 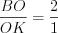 ,
, 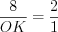 и
и 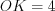 .
.
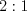 , считая от его вершины, то
, считая от его вершины, то 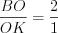 ,
, 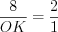 и
и 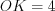 .
.А так как 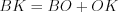 , то
, то 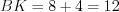 .
.
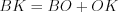 , то
, то 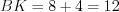 .
.Ответ: 12.
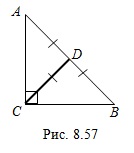
Пример 8. Медиана  , проведенная к гипотенузе равнобедренного прямоугольного треугольника
, проведенная к гипотенузе равнобедренного прямоугольного треугольника  (рис. 8.57) равна 7. Найдите катеты этого треугольника.
(рис. 8.57) равна 7. Найдите катеты этого треугольника.
 , проведенная к гипотенузе равнобедренного прямоугольного треугольника
, проведенная к гипотенузе равнобедренного прямоугольного треугольника  (рис. 8.57) равна 7. Найдите катеты этого треугольника.
(рис. 8.57) равна 7. Найдите катеты этого треугольника.
Решение. Так как медиана проведена к гипотенузе треугольника, то 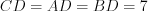 .
.
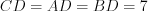 .
.Поскольку треугольник  равнобедренный, то его катеты равны, а медиана, проведенная к основанию
равнобедренный, то его катеты равны, а медиана, проведенная к основанию  треугольника, является и высотой этого треугольника.
треугольника, является и высотой этого треугольника.
 равнобедренный, то его катеты равны, а медиана, проведенная к основанию
равнобедренный, то его катеты равны, а медиана, проведенная к основанию  треугольника, является и высотой этого треугольника.
треугольника, является и высотой этого треугольника.Тогда по теореме Пифагора 8.3 :
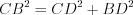 ,
, 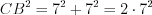 , а
, а  .
. Ответ: 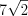 и
и 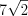 .
.
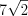 и
и 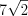 .
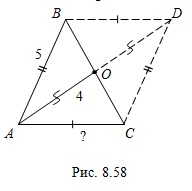
.Пример 9. В равнобедренном треугольнике с боковой стороной равной 5 см проведена медиана боковой стороны. Найдите основание треугольника, если медиана равна 4 см.

Решение. Рассмотрим равнобедренный треугольник  с боковым сторонами
с боковым сторонами 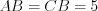 см и медианой
см и медианой 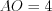 см (рис. 8.58).
см (рис. 8.58).
 с боковым сторонами
с боковым сторонами 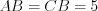 см и медианой
см и медианой 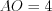 см (рис. 8.58).
см (рис. 8.58).Достроим треугольник  до параллелограмма
до параллелограмма 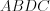 , тогда диагональ параллелограмма
, тогда диагональ параллелограмма 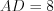 см.
см.
 до параллелограмма
до параллелограмма 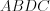 , тогда диагональ параллелограмма
, тогда диагональ параллелограмма 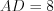 см.
см.По свойству диагоналей параллелограмма получим: 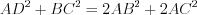 или
или  , откуда
, откуда 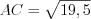 см.
см.
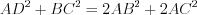 или
или  , откуда
, откуда 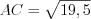 см.
см.Ответ: 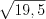 см.
см.
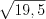 см.
см.Пример 10. На рисунке 8.59 отрезки 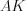 и
и 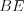 – медианы треугольника
– медианы треугольника  . Площадь треугольника
. Площадь треугольника 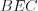 равна 5. Найдите площади треугольников
равна 5. Найдите площади треугольников 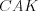 и
и  .
.
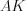 и
и 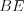 – медианы треугольника
– медианы треугольника  . Площадь треугольника
. Площадь треугольника 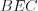 равна 5. Найдите площади треугольников
равна 5. Найдите площади треугольников 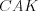 и
и  .
.
Решение. Так как медиана делит треугольник на два равновеликих треугольника, то 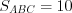 , а
, а 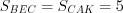 .
.
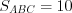 , а
, а 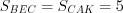 .
.Ответ: 10; 5.
Пример 11. В треугольнике  (рис. 8.60)
(рис. 8.60) 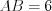 ,
, 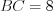 и
и 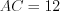 . Найдите длины отрезков, на которые биссектриса
. Найдите длины отрезков, на которые биссектриса 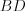 делит сторону треугольника
делит сторону треугольника 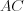 .
.
 (рис. 8.60)
(рис. 8.60) 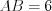 ,
, 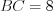 и
и 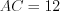 . Найдите длины отрезков, на которые биссектриса
. Найдите длины отрезков, на которые биссектриса 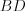 делит сторону треугольника
делит сторону треугольника 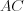 .
.
Решение. Так как биссектриса треугольника делит сторону этого треугольника на отрезки пропорциональные двум другим его сторонам, то 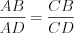 .
.
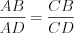 .
. Если положим, что 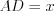 , то
, то 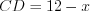 , тогда:
, тогда: 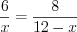 ,
, 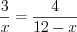 , откуда
, откуда 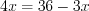 ,
, 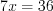 ,
,  ,
, 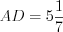 , а
, а  .
.
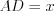 , то
, то 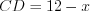 , тогда:
, тогда: 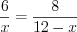 ,
, 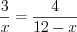 , откуда
, откуда 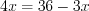 ,
, 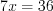 ,
,  ,
, 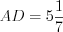 , а
, а  .
. Ответ: 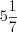 и
и 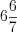 .
.
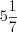 и
и 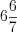 .
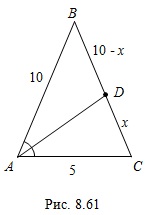
.Пример 12. В равнобедренном треугольнике основание и боковая сторона соответственно равны 5 см и 10 см. Найдите биссектрису угла при основании треугольника.

Решение. Рассмотрим равнобедренный треугольник  с основанием
с основанием 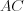 (рис. 8.61). Согласно условию задачи
(рис. 8.61). Согласно условию задачи 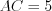 см,
см, 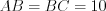 см.
см.
 с основанием
с основанием 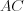 (рис. 8.61). Согласно условию задачи
(рис. 8.61). Согласно условию задачи 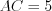 см,
см, 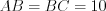 см.
см.Проведем биссектрису  угла
угла 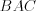 . Полагая
. Полагая  см, запишем
см, запишем 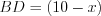 cм. По свойству биссектрисы треугольника получим:
cм. По свойству биссектрисы треугольника получим: 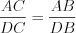 ,
, 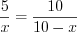 ,
, 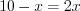 ,
, 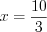 см.
см.
 угла
угла 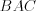 . Полагая
. Полагая  см, запишем
см, запишем 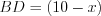 cм. По свойству биссектрисы треугольника получим:
cм. По свойству биссектрисы треугольника получим: 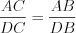 ,
, 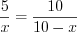 ,
, 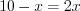 ,
, 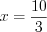 см.
см.Ответ: 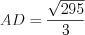 см.
см.
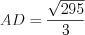 см.
см.Пример 13. Площадь правильного треугольника равна 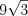 . Найдите высоту этого треугольника.
. Найдите высоту этого треугольника.
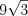 . Найдите высоту этого треугольника.
. Найдите высоту этого треугольника. Ответ: 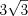 .
.
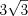 .
.Пример 14. Площадь прямоугольного треугольника равна 36, а один из его катетов равен 8. Найдите высоту треугольника, проведенную к гипотенузе.
По теореме Пифагора 8.3 найдем гипотенузу: 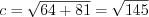 .
.
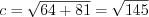 .
.Но, с другой стороны, 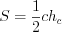 . Тогда
. Тогда 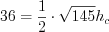 , откуда
, откуда 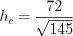 .
.
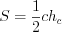 . Тогда
. Тогда 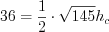 , откуда
, откуда 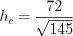 .
. Ответ: 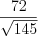 .
.
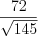 .
.Пример 15. Боковая сторона равнобедренного треугольника равна 5, а угол при основании треугольника равен 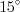 (рис. 8.62). Найдите площадь этого треугольника.
(рис. 8.62). Найдите площадь этого треугольника.
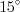 (рис. 8.62). Найдите площадь этого треугольника.
(рис. 8.62). Найдите площадь этого треугольника.
Решение. Поскольку углы при основании равнобедренного треугольника равны, то найдем угол при вершине этого треугольника: 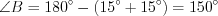 .
.
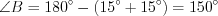 .
.По формуле 8.11 найдем площадь треугольника: 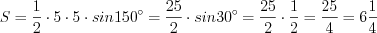 .
.
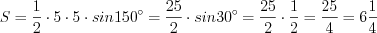 .
. Ответ: 6,25.
Пример 16. Найдите площадь треугольника, стороны которого равны 6, 10 и 12.
Решение. Найдем полупериметр этого треугольника: 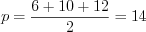 .
.
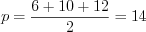 .
.Ответ: 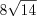 .
.
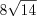 .
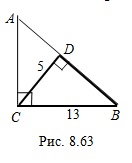
. Пример 17. В треугольнике  (рис. 8.63) катет
(рис. 8.63) катет 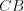 равен 13, а высота
равен 13, а высота  равна 5. Найдите периметр этого треугольника.
равна 5. Найдите периметр этого треугольника.
 (рис. 8.63) катет
(рис. 8.63) катет 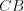 равен 13, а высота
равен 13, а высота  равна 5. Найдите периметр этого треугольника.
равна 5. Найдите периметр этого треугольника. 
Найдем периметр треугольника 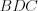 :
: 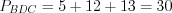 .
.
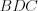 :
: 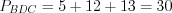 .
. Так как 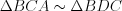 (по двум углам), то их стороны пропорциональны:
(по двум углам), то их стороны пропорциональны: 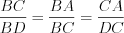 ,
,  ,
,  .
.
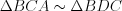 (по двум углам), то их стороны пропорциональны:
(по двум углам), то их стороны пропорциональны: 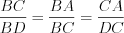 ,
,  ,
,  .
. Так как отношение периметров подобных треугольников равно коэффициенту подобия, то 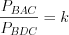 . Тогда
. Тогда 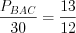 ,
,  , откуда
, откуда 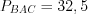 .
.
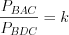 . Тогда
. Тогда 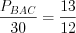 ,
,  , откуда
, откуда 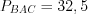 .
.Ответ: 32,5.
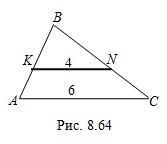
Пример 18. Площадь треугольник 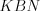 (рис. 8.64) равна 30. Параллельно стороне
(рис. 8.64) равна 30. Параллельно стороне 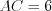 проведен отрезок
проведен отрезок 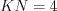 . Найдите площадь треугольника
. Найдите площадь треугольника  .
.
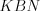 (рис. 8.64) равна 30. Параллельно стороне
(рис. 8.64) равна 30. Параллельно стороне 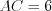 проведен отрезок
проведен отрезок 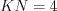 . Найдите площадь треугольника
. Найдите площадь треугольника  .
.
Решение. Так как 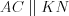 , то
, то 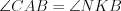 , а
, а 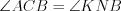 , следовательно,
, следовательно, 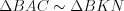 (по двум углам).
(по двум углам).
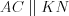 , то
, то 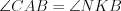 , а
, а 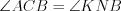 , следовательно,
, следовательно, 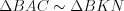 (по двум углам).
(по двум углам).Тогда 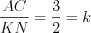 ,
, 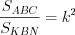 ,
, 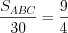 , откуда
, откуда  .
.
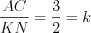 ,
, 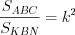 ,
, 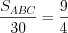 , откуда
, откуда  .
. Ответ: 67,5.
1. Треугольники можно классифицировать:
1) по сторонам: разносторонний, равнобедренный и равносторонний;
2) по углам: остроугольный, прямоугольный и тупоугольный.
2. Существуют формулы, которые устанавливают взаимосвязь между углами и сторонами треугольников:
1) в произвольном треугольнике: теорема синусов и теорема косинусов;
2) в прямоугольном треугольнике: теорема Пифагора.
3. В любом треугольнике можно провести три высоты, три медианы и три биссектрисы.
4. Различайте: равные и равновеликие треугольники.


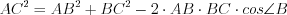 или
или 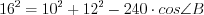 , откуда
, откуда 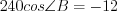 , а
, а 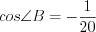 .
.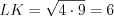 (см). Так как
(см). Так как 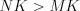 , то
, то 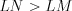 .
.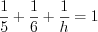 , откуда
, откуда 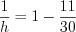 ,
, 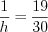 ,
, 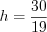 .
.  ,
, 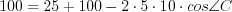 , откуда
, откуда 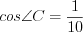 .
. . По теореме косинусов
. По теореме косинусов 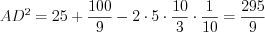 , откуда
, откуда 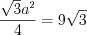 ,
, 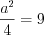 ,
, 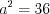 ,
, 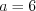 .
. и
и 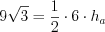 ,
, 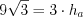 ,
, 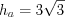 .
.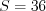 ,
,  , то
, то 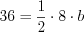 ,
, 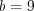 .
.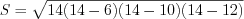 ,
, 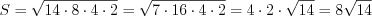 .
.